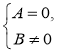Дроби. Дробові вирази. Раціональні вирази. Допустимі значення змінних
Тема. Дроби. Дробові вирази. Раціональні вирази. Допустимі значення змінних
Мета: домогтися засвоєння учнями змісту понять: цілий вираз, дробовий вираз, раціональний вираз, раціональний дріб, допустимі значення змінної у виразі; сформувати в учнів уміння виділяти названі види виразів серед запропонованих виразів зі змінними, а також виконувати дії, що мають на меті знаходження ОДЗ дробового виразу.
Тип уроку: засвоєння знань, умінь та навичок.
Наочність та обладнання: опорний конспект «Дробові вирази. Раціональні вирази».
Хід уроку
I. Організаційний етап
Вступне слово вчителя
- Особливості вивчення алгебри у 8 класі;
- організація навчального процесу;
- будова підручника.
II. Перевірка домашнього завдання
Вчитель перевіряє літнє домашнє завдання (якщо таке було задано).
III. Формулювання мети і завдань уроку
З метою усвідомлення учнями необхідності вивчення питання про види раціональних виразів пропонуємо учням завдання:
Який із виразів: х2, х + 2ху, ![]() ,
, ![]() зайвий? Чому?
зайвий? Чому?
Після обговорення з учнями результатів виконання запропонованого завдання формується думка: у 7 класі було вивчено питання про види, властивості і способи перетворення виразів, що не містять ділення на змінну (цілі вирази); у 8 класі настав час вивчити види, властивості і способи перетворень виразів, що містять ділення на змінну (дробові вирази), а також узагальнити знання учнів про види виразів та логічний зв'язок між ними. Цей висновок і є основною дидактичною метою вивчення розділу.
IV. Актуалізація опорних знань та вмінь
метою успішного сприйняття учнями навчального матеріалу уроку перед вивченням нової теми слід активізувати знання учнів про алгоритми виконання дій з раціональними числами, способи перетворення цілих раціональних виразів та способи розв'язання лінійних рівнянь та рівнянь, що зводяться до лінійних (вивчені у 7 класі).
Виконання усних вправ
- Знайдіть значення виразів:
1 – ![]() ;
; ![]() – 2;
– 2; ![]() ; -27 : 81; -3,7 – 0,4;
; -27 : 81; -3,7 – 0,4; ![]() – 0,2;
– 0,2; 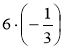 ;
; 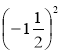 .
.
-
Обчисліть:
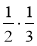 ;
; 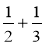 ;
; 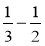 ;
; 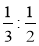 ;
; 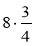 ;
; 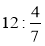 ; 19 · 0,1; 7 : 0,1;
; 19 · 0,1; 7 : 0,1; 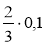 ;
; 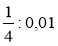 .
.
-
При якому значенні змінної значення виразу дорівнює нулю:
х – 1; у + 3, а2; х2 + 4; а(а – 1); х(х + 3); 2x – 1; 5у(у + 1); |х|; |х – 3|; |х| – 1? -
Спростіть вирази: х5 · х;
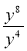 ; 5 – (х + 3); 2,5 + (у – 0,5).
; 5 – (х + 3); 2,5 + (у – 0,5).
- Подайте вирази у вигляді добутку:
а2 – b2; ху – х2; а2b – аb; х3 – у3; с2 – 2cd + d2; а3 + b3.
- Перетворіть вирази в многочлен стандартного вигляду:
а(а – 3); -с(х – у + а); (х + 1)(х – 3); (а – 4)(4 + а); (х+2)2;
(а – b)(а2 + аb + b2).
V. Засвоєння знань
План вивчення нового матеріалу
- Цілі вирази.
- Дробові вирази.
- Раціональні вирази.
- Раціональний дріб.
- Допустимі значення змінних у виразі (ОДЗ).
|
Конспект 1 |
|
|
Дробові вирази. Раціональні вирази |
|
|
|
|
Приклад. a + b; 2а3; 3х(х – у)3; b; 5 — цілі вирази. |
|
|
!Будь-який цілий вираз можна подати у вигляді многочлена. |
|
|
|
|
Приклад. |
|
|
|
|
|
|
Дріб |
|
|
Приклад. |
|
|
|
|
!Для раціонального дробу |
|
|
Приклад. Для виразу |
|
|
|
|
|
Отже, ОДЗ змінної а у виразі |
|
|
ОДЗ: а ≠ ±2 (або а ≠ 2 і а ≠ -2, або всі значення а, крім а = 2 та а = -2). |
|
|
|
|
|
(або |
|
|
Щоб знайти значення змінної, при якому раціональний дріб |
|
|
а) знайти ОДЗ дробу (з умови В ≠ 0); |
|
|
б) прирівняти чисельник до нуля (А = 0) і знайти відповідні значення змінних; |
|
|
в) із значень, здобутих в п. б) вилучити ті, що не війшли до ОДЗ (див. п. а.). |
|
|
Приклад. При якому значенні змінної дріб |
|
|
Розв'язання |
|
|
1) ОДЗ: х – 4 ≠ 0; х ≠ 4; |
|
|
2) х2 – 16 = 0; (х – 4)(х + 4) = 0; х = 4 або х = - 4. |
|
|
3) х = 4 не входить до ОДЗ, тому при х = - 4 дріб |
|
Вивчення матеріалу уроку починається із повторення видів цілих виразів, що їх вивчали учні в 7 класі (одночлени, многочлени), та узагальнення уявлень учнів про їх структуру та властивості (усі цілі вирази містять 5 арифметичних дій, крім ділення на вираз зі змінними, та можуть бути представлені у вигляді многочлена).
Як протилежність цілим виразам розглядаються вирази, що, крім інших арифметичних дій, містять ділення на змінну – таким чином формується уявлення учнів про зміст поняття дробового виразу, після чого розглядається поняття раціонального виразу як загального виду виразів, що поділяється на цілі та дробові вирази.
Далі формується уявлення учнів про зміст поняття раціонального дробу як особливого випадку дробового виразу та про зміст поняття допустимого значення змінної у виразі та області допустимих значень змінної (ОДЗ) у виразі (при цьому можна спиратись на набуті учнями в 7 класі знання про зміст поняття області визначення функції).
VI. Засвоєння знань та вмінь
Виконання усних вправ
- Які з виразів є цілими; дробовими? Які з виразів є дробами; раціональними дробами?
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) 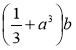 ; д)
; д) ![]() ; є)
; є) ![]() .
.
-
Знайдіть значення виразу
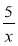 при х = 5, х = -5, х = -0,1.
при х = 5, х = -5, х = -0,1.
- При яких значеннях змінної вираз не має змісту? Назвіть допустимі значення змінної у виразі:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
-
Які з наведених рівностей є тотожностями?
а)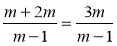 ; б)
; б) 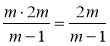 ; в)
; в) 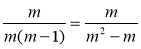 .
.
Виконання письмових вправ
Для реалізації дидактичної мети на цьому уроці слід розв'язати завдання такого змісту:
- Серед поданих виразів зі змінними вибрати: цілі, дробові вирази, раціональні дроби.
1) Які з виразів є цілими; дробовими? Які з виразів є дробами; раціональними дробами?
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) 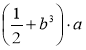 ; д)
; д) ![]() ; є)
; є) ![]() .
.
2) Які з виразів![]() а2b; (х – у)2 – 4ху;
а2b; (х – у)2 – 4ху; ![]() ;
; ![]() ;
; ![]() ; (с + 3)2 +
; (с + 3)2 + ![]() є цілими, які — дробовими?
є цілими, які — дробовими?
3) Із раціональних виразів
7х2 – 2ху; ![]() ;
; ![]() ; а(а – b) –
; а(а – b) – ![]() ;
; ![]() ;
; ![]() випишіть ті, які є:
випишіть ті, які є:
а) цілими виразами; б) дробовими виразами.
4) Складіть дріб:
а) чисельник якого є добутком змінних х і у, а знаменник — сумою;
б) чисельник якого є різницею змінних а і b, а знаменник — добутком.
- Знаходження значень дробового виразу при даних значеннях змінних.
1) Знайдіть значення виразу:
а) ![]() при x = 0; х = 5; х = -3; б)
при x = 0; х = 5; х = -3; б) ![]() при а = 4, b = 2; а = -4, b = 6;
при а = 4, b = 2; а = -4, b = 6;
в) ![]() при а = -2; г)
при а = -2; г) ![]() при b = 3;
при b = 3;
д) ![]() при x =
при x = ![]() ; є)
; є) ![]() при у = 1,5.
при у = 1,5.
2) Чому дорівнює значення дробу ![]() при:
при:
а) a = -3, b = -1; б) a = 1![]() , b = 0,5?
, b = 0,5?
- Знаходження допустимих значень змінних у виразі.
1) Укажіть допустимі значення змінної у виразі:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
2) Знайдіть допустимі значення змінної у виразі:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
- Складання виразів зі змінними за умовою задачі.
Автомобіль проїхав 195 км за? год. Запишіть у вигляді виразу швидкість автомобіля. Знайдіть значення цього виразу при t = 3.
-
Виконання вправ на повторення: арифметичні дії зі звичайними
дробами (скорочення, порівняння, додавання, віднімання), розкладання цілих виразів на множники із застосуванням різних способів.
1) Перетворіть у многочлен:
а) (х – 10)(х + 10); б) (2а + 3)(2а – 3); в) (y – 5b)(y + 5b);
г) (8x + y)(y – 8x); д) (х + 7)2; є) (b + 5)2; ж) (а – 2х)2; з) (ab – 1)2.
2) Розкладіть многочлен на множники:
а) 15ах + 20ау; б)36bу – 9су; в) х2 – ху; г) ху – у2; д) а2 +5ab; е) 15с – 10с2.
3) Розкладіть на множники:
а) х2 – 25; б) 16 – с2; в) а2 – 6a + 9; г) х2 + 8х + 16; д) а3 – 8; є) b3 + 27.
- Для учнів, які мають достатній і високий рівень знань — виконання завдань підвищеного рівня складності та логічні вправи. Вставте пропущений вираз:
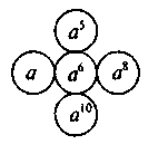
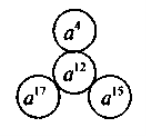
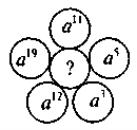
VII. Підсумки уроку
Контрольні запитання
1) Які вирази називають цілими? Наведіть приклади.
2) Які вирази називають дробовими? Наведіть приклади.
3) Які вирази називають раціональними? Які з наведених раціональних виразів цілі, а які дробові: 3а, ![]() ,15р2q,
,15р2q, ![]() ,
, ![]() ,
, ![]() ?
?
VIII. Домашнє завдання
- Вивчити означення понять, розглянутих на уроці.
- Розв'язати вправи на: класифікацію раціональних виразів, знаходження ОДЗ виразів, обчислення значень виразів зі змінними та числових виразів, що містять звичайні дроби, розв'язання цілих рівнянь.


про публікацію авторської розробки
Додати розробку