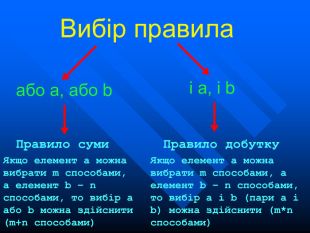
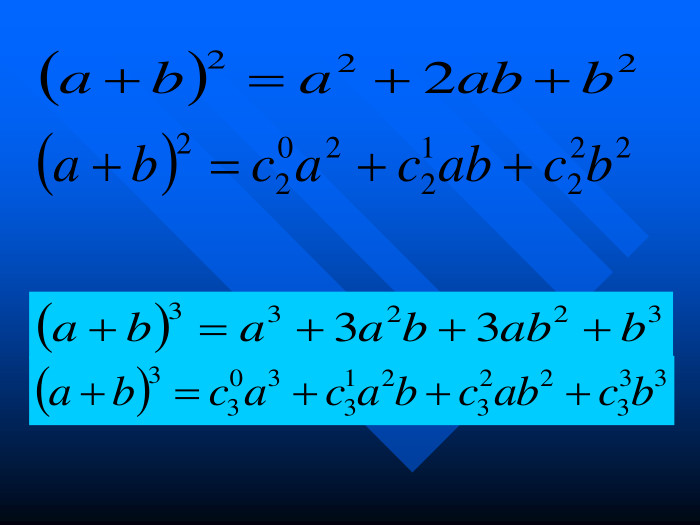Елементи комбінаторики
Про матеріал
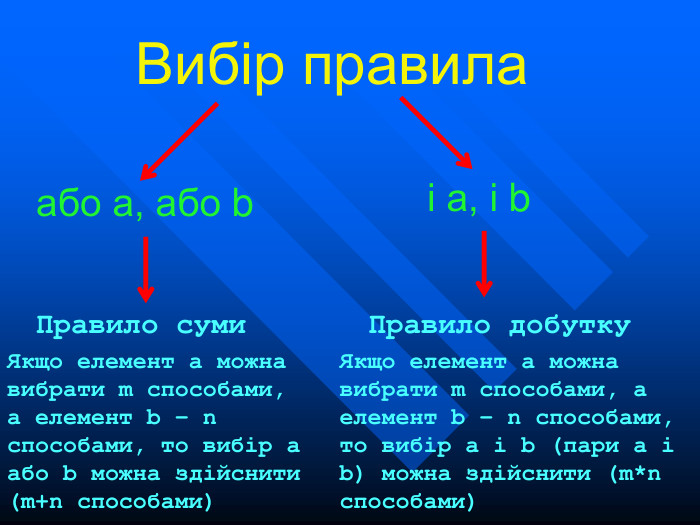
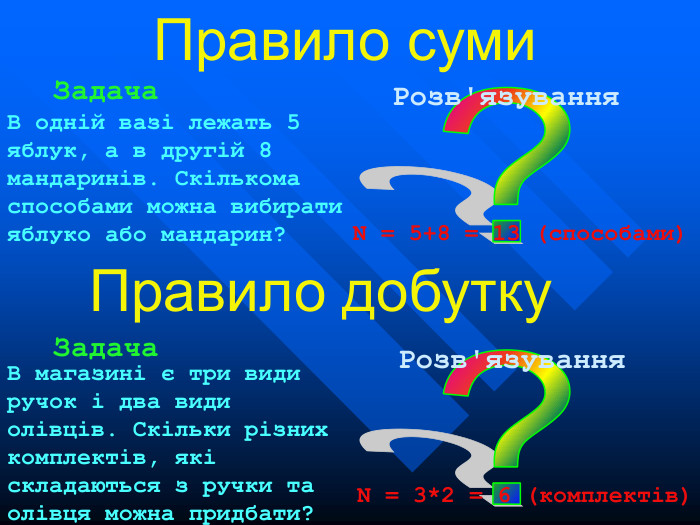
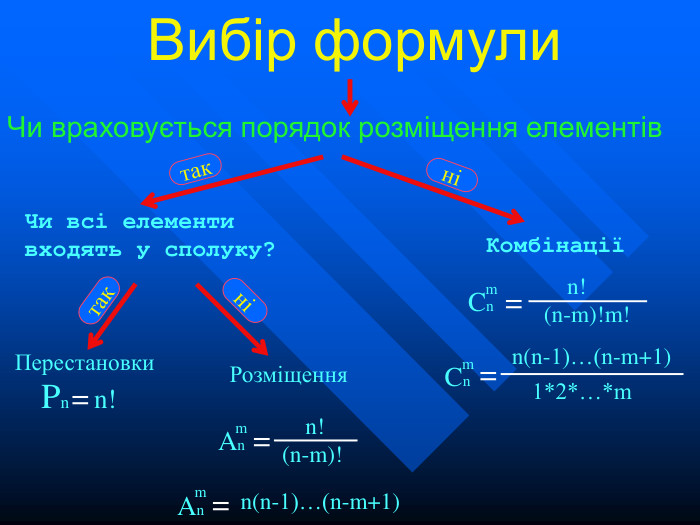
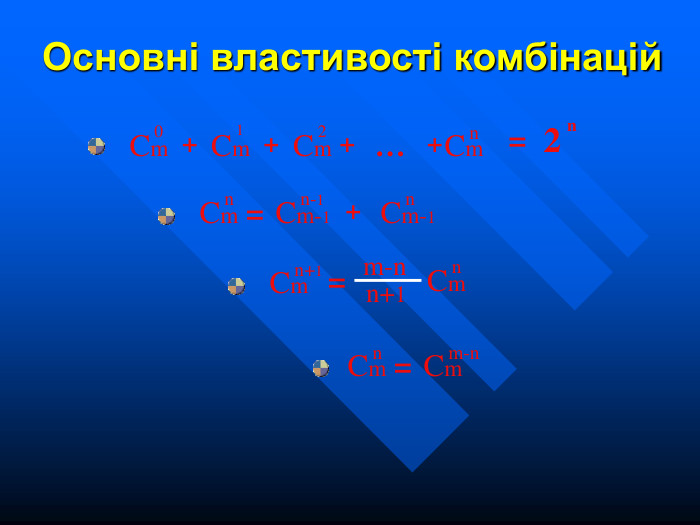
Презентація на тему "Елементи комбінаторики". Розязування задач на розміщення, перестановки та комбінації.
Перегляд файлу
Зміст слайдів


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку