Елементи комбінаторики. Комбінаторні правила суми і добутку. Розв’язування вправ.

Тема.    Елементи комбінаторики. Комбінаторні правила суми і добутку.     

              Розв’язування вправ.

Мета.  

• Формування предметної компетентності: формувати знання студентів про множину та її елементи, про операції над множинами; ознайомити студентів із видами сполук, вчити розрізняти їх і знаходити їх число за відповідними формулами; домогтися засвоєння комбінаторних правил суми та добутку; сформувати вміння розв’язувати задачі, що передбачають застосування цих правил.

• Формування ключових компетентностей:

- cпілкування державною мовою: доречно та коректно вживати в мовленні математичну термінологію;

- інформаційно – цифрова компетентність: уміння діяти за алгоритмом, вміння використовувати математичні методи у життєвих ситуаціях;

- уміння вчитися протягом життя – визначати мету навчальної діяльності, відбирати і застосовувати потрібні знання та способи діяльності для досягнення мети.

Тип заняття:  засвоєння нових  знань.

Обладнання:

А. Наочні посібники: портрети, відеофільми про Дж. Кардано, Н. Тарталья,

Г. Галілея,  Б. Паскаля,  П. Ферма та Г.Лейбніца, таблиця з основними формулами комбінаторики

Б. ТЗН: проектор, екран.

В. Література:  Математика : алгебра і початки аналізу та геометрія, рівень стандарту : підруч. для 11 кл. закладів загальної середньої освіти / А. Г. Мерзляк, Д. А. Номіровський, В. Б. Полонський та ін. — Х. : Гімназія, 2019. — 208 с.

Математика: 11: підруч. Для загальноосвіт.навч.закл.: рівень стандарту /Г.П.Бевз, В.Г.Бевз. – К. : Генеза, 2011. – 320с.: іл. – Бібліо294.гр. : с.

 

Епіграф заняття.

 «Як крапля довбає камінь не силою,

 а частим падінням, так і людина

стає вченою частим учінням».
                                                                       

                                             Дістервег

 

 

Хід заняття.

І. Організаційний момент. (Перевірка присутності студентів на занятті та їх готовності до заняття).

ІІ. Мотивація навчальної діяльності.

       Із завданнями, які отримали назву комбінаторних, люди стикалися з глибокої давнини. Вже кілька тисячоліть тому в Стародавньому Китаї захопилися складанням магічних квадратів, в яких задані числа розташовувалися так, що їх сума по всіх горизонталях, вертикалях і головних діагоналях була однією і тією ж. У Древній Греції підраховували кількість різних комбінацій довгих і коротких слів у віршованих розмірах, займалися теорією фігурних чисел, вивчали фігури, які можна скласти з частин особливим чином розрізаного квадрата і т.д.

       Комбінаторні задачі виникли і у зв'язку з такими іграми, як шашки, шахи, доміно, карти, кістки і т.д.

        Комбінаторика стає наукою лише в 18 столітті - у період, коли виникла теорія ймовірностей. Щоб вирішувати теоретико-імовірнісні задачі, потрібно було вміти підраховувати кількість різних комбінацій, підлеглих тим або іншим умовам. Після перших робіт, виконаних у 18 столітті  італійським вченим Дж. Кардано, Н. Тарталья, і Г. Галілеєм, такі завдання вивчали французькі математики Б. Паскаль і П. Ферма. Першим розглядав комбінаторику як самостійну галузь науки німецький філософ і математик Г. Лейбніц, який опублікував в 1666 році роботу "Про мистецтво комбінаторики", в якій вперше з'являється сам термін "комбінаторний".

      Чудові досягнення в області комбінаторики належать Л. Ейлеру. Комбінаторними завданнями цікавилися і математики, які займалися складанням та розгадуванням шифрів, вивченням древніх писемностей. Тепер комбінаторика знаходить застосування у всіх галузях науки і техніки: в біології, де вона застосовується для вивчення складу білків і ДНК, в хімії, в механіці .

ІІІ. Сприймання і усвідомлення матеріалу про множини та операції над множинами.

1. Поняття множини

Поняття множини належить до первісних, воно не означається. Найбільший вклад у створення теорії множин вніс Г. Кантор. Множина — це сукупність, зібрання деяких предметів будь-якої природи, наприклад: множина учнів класу, множина цифр десяткової нумерації, множина букв українського алфавіту, множина міст держави, множина будинків на вулиці тощо.

Для позначення множин використовуються прописні літери латинського алфавіту або фігурні дужки: множина А або {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}.

2. Елементи множини

Означення 1. Предмети, з яких складається множина, називаються її елементами.

Наприклад, а =5 — елемент множини цифр десяткової нумерації;

Чортків — елемент множини міст України.

Якщо множину цифр десяткової нумерації позначити через А, то належність числа цій множині можна позначити так: 5 А, 9 А.

Число 12 не належить множині А, не є елементом цієї множини. Це твердження можна записати так: 12 А.

Множини бувають скінченні (множина будинків на певній вулиці) і нескінченні (множина точок прямої).

Означення 2. Множина, у якій немає жодного елемента, називається порожньою.

Позначається .

Наприклад, множина розв’язків  рівняння х² = -1 на множині дійсних чисел є порожньою, х .

Множину можна задати: переліченням усіх її елементів, наприклад

{а, b, с}або характеристичною властивістю, наприклад, В — множина чисел, кратних 15, що менші від 90.

3. Підмножина

Означення 3. Дві множини називаються рівними, якщо вони складаються з однакових елементів.

Наприклад, X— множина коренів рівнянняx²=25, Х={-5;5};

множина Y— множина коренів рівняння | х | = 5, Y= {-5; 5}.

Х= Y.

Означення 4. Якщо множина В складається з деяких елементів даної множини А і лише з них, то множина В називається підмножиною множини А.

Позначаємо це так: В А.

Наприклад, якщо В = {1, 2, 3}, А = {1, 2, 3, 4}, то В А.

Порожня множина є підмножиною будь-якої множини.

4. Операції над множинами

Над множинами можна виконувати певні операції. Розглянемо три з них.

Операції над множинами наочно демонструються за допомогою діаграм Ейлера, де множини зображені кругами.

Переріз множин

Означення 5. Перерізом множин А і В називається множина С, яка складається з усіх тих і лише тих елементів, які належать кожній із даних множин.

Позначаємо це так: А В = С .

  

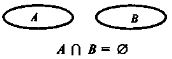
Приклад 1. А — множина всіх дільників числа 32, В — множина всіх дільників числа 24.

А = {1, 2, 4, 6, 8, 16, 32}, B = {1, 2, 3, 4, 6, 8, 12, 24}.

С = А В, С = {1, 2, 4, 8}.

Об'єднання множин

Означення 6. Об'єднанням або сумою двох множин А і В називається така множина R, яка складається з усіх елементів множин А і В і лише з них.

Позначаємо це так: АВ = R.

 

Кожний зі спільних елементів береться в множину лише один раз.

Приклад 2. Для множин А і В з прикладу 1 об'єднанням буде

R= А В = {1, 2, 3, 4, 6, 8, 12, 16, 24, 32}.

Приклад 3. Множина дійсних чисел є об’єднанням множин раціональних та ірраціональних чисел: QI = R.

Віднімання множин.

Означення 7. Різницею двох множин А і В називається така множина D яка складається з усіх елементів множини А, які не належать множині В. Записуємо D = А\В.

Приклад 4. А = {5, 6, 8, 12}, В = {5, 6}, D = {8,12}.

Упорядкована множина

Означення 8. Скінченна множина, для якої істотний порядок елементів, називається впорядкованою.

Вказати порядок розміщення елементів у скін­ченній множині з л елементів — означає поставити у відповідність кожному елементу даної множини певне натуральне число від 1 до п.

Приклад 7. Множини А = {1, 2, 7} і В = {2, 7, 1} є рівними, якщо вони не впорядковані, А= В.

Якщо ж вони є впорядкованими, то А ≠В.

Приклад 8. Із 30 учнів класу потрібно вибрати двох:

а)старосту і його заступника;

б)для чергування у класі.

У випадку а) — це впорядкована множина.

 

5. Числові множини.

      Числові множини – це множини елементами яких є числа.

• Множина натуральних чисел, тобто чисел, які виникають в процесі лічби. Цю множину чисел позначають буквою N. N=(1, 2, 3, 4, 5…).
• Об’єднання натуральних чисел, чисел протилежних до натуральних і числа 0 утворює множину цілих чисел, яку позначають буквою Z. 

     Z=(0, ±1, ±2, ±3…).

• Множина раціональних чисел(її позначають буквою Q) – це множина чисел, які можна подати у вигляді нескоротного дробу. Кожне раціональне число можна подати у вигляді нескінченного періодичного дробу.
• Числа, які подаються у вигляді нескінченного неперіодичного дробу, утворюють множину ірраціональних чисел.

ІV. Сприймання і усвідомлення поняття  факторіала.

Означення. Факторіал — це добуток послідовних натуральних чисел.

п! = 1 ∙ 2 ∙ 3  ∙ ... ∙ n.

Наприклад : 1! = 1;

2! = 1 ∙ 2 = 2;

3! = 1 ∙ 2 ∙ 3 = 6;

4! = 1 ∙ 2 ∙ 3 ∙ 4 = 3! ∙ 4 = 24.

Приймають, що 0! = 1.

Термін «факторіал» походить від англійського слова «фактор» — множник.

Приклади розв’язування задач

1. Обчислити.

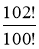Розв'язання

.

2. Спростити:а)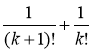; б) .

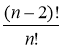Розв'язання

а) .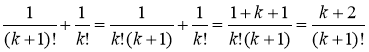

б) .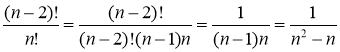

3. Розв'язати рівняння .

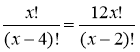Розв'язання

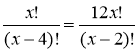
ОДЗ: х ≥ 4, х N.

,

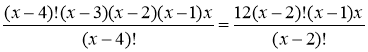(х–3)(х–2)(х– 1)х–12(х– 1)х = 0,

(x–1)x(x²–5х– 6) = 0,

х–1≠0, x≠0; х²–5х–6 = 0;

х₁ =-1,х₂= 6. x₁ ОДЗ.

Відповідь: х = 6.

     На практиці часто доводиться відповідати на запитання: скількома способами можна виконати певне завдання? Наприклад, скласти розклад п'яти уроків на день із десяти різних предметів; позначити різні зв'язки між атомами і молекулами певної речовини; записати діагоналі опуклого десятикутника;

знайти різні шляхи доставки виробів із заводу в магазин і визначити, який з них найбільш вигідний.

      В задачах в яких мова йде про комбінування об’єктів, їх називають комбінаторними задачами,  а розділ математики, в якому вивчаються питання про те, скільки різних комбінацій, що відповідають тим чи іншим умовам можна скласти із заданих об’єктів, називають комбінаторикою.

     Під час розв’язування комбінаторних задач доводиться розглядати скінченні множини, складені з елементів будь-якої природи, та їх підмножини. Залежно від умови задачі розглядаються скінченні множини, в яких істотним є або порядок елементів, або їх склад, або перше і друге одночасно. Вибрані групи елементів називають сполуками.

     Такі скінченні множини дістали певну назву: перестановки, розміщення, комбінації.

V. Сприймання і усвідомлення поняття перестановки, розміщення, комбінації.

 

1.  Перестановки.

Означення. Будь-яка впорядкована множина, що складається з п елементів, називається перестановкою з п елементів.

Перестановки відрізняються одна від одної лише порядком елементів.

Приклад 1. Із елементів множини А = {1, 2, 7} можна утворити 6 перестановок: {1, 2, 7}, {1, 7, 2}, {2, 1, 7}, {2, 7, 1}, {7, 1, 2}, {7, 2, 1}.

Перестановки — впорядковані множини.

Кількість усіх можливих перестановок у множині з п елементів позначається Р_n.

Взагалі, кількість усіх можливих перестановок у множині з п елементів дорівнює добутку послідовних натуральних чисел, тобто

Р_n= 1 ∙ 2 ∙ 3 ∙ 4 ∙ ... ∙n,

Р_n=п!,      (1)

де п — натуральне число.

Приклад 2. Скільки семицифрових чисел можна утворити за допомогою семи різних цифр, відмінних від 0, не повторюючи цифри у запису числа?

Розв'язання

Шукане число дорівнює кількості перестановок із 7 різних елементів:

Р₇ = 1 ∙ 2 ∙ 3 ∙ 4 ∙ 5 ∙ 6 ∙ 7 = 5040.

Відповідь: 5040 різних семицифрових чисел.

 

2.  Розміщення.

 

Означення. Упорядкована підмножина з п елементів даної множини М, що містить т елементів, де п ≤ т, називається розміщенням з т елементів по п.

Кількість усіх можливих розміщень з m елементів по n елементів позначається і обчислюється за формулою 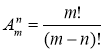                                                      (2)

Розміщення відрізняються один від одного або елементами, або їх порядком. Якщо m = n, маємо перестановку з т елементів, тобто перестановка є окремим випадком розміщення за умови, що т = п.

 

Приклад 1.     Скільки можна утворити різних двоцифрових чисел із чотирьох цифр 1, 3, 7, 9, не повторюючи їх?

Розв'язання

Потрібно утворити впорядковані множини з двох елементів:

13, 31, 17, 71, ... .

Ці множини є розміщеннями з 4 елементів по 2, тобто кількість
двоцифрових чисел, що відповідають умові, становитиме = 4 ∙ 3 = 12.

Відповідь:  12.

 

 

3. Комбінації.

Означення 1. Будь-яка підмножина з п елементів даної множини М, що містить т елементів, називається комбінацією з т елементів по п.

Порядок елементів у множині неістотний, комбінації відрізняються лише складом елементів. Кількість усіх можливих комбінацій з т елементів по n позначається символом і обчислюється за формулою 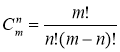.        (3)

Комбінація відрізняється від розміщення тим, що у цій підмножині неістотним є порядок елементів.

Приклад 1. На площині позначено n точок, з яких ніякі три не лежать на одній прямій. Скільки різних прямих можна провести через ці точки?

Розв'язання

Оскільки через кожну пару точок можна провести лише одну пряму, то кількість різних прямих дорівнює кількості комбінацій з n елементів по 2 елементи, тобто .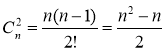

 

Приклад 2. Обчислити .

Розв’язання.

.

 

VІ. Комбінаторні задачі.

 

     Розв’язування  простих комбінаторних задач зводиться до визначення виду сполуки, про яку йдеться в задачі, і застосування відповідної формули для обчислення кількості цих сполук. Тут основна трудність, яка виникає в студентів, -  саме визначення виду сполуки. Тому перед розв’язуванням задач на обчислення кількості різних сполук потрібно запропонувати студентам схему, що сприятиме правильному визначенню виду сполуки, про яку йдеться в умові задачі. При цьому враховуються характеристичні властивості кожного виду сполук.

Вибір формули

для обчислення кількості сполук.

 

 

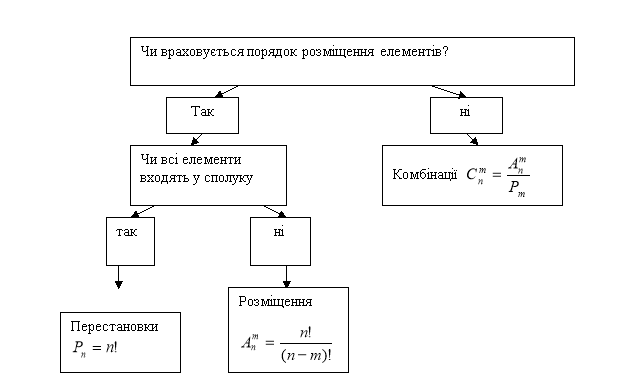
Задача 1.

      Потрібно виділити трьох з п’яти студентів на чергування до їдальні. Скількома способами це можна зробити?

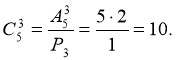
Задача 2.

     В одинадцятому класі 35 учнів. Вони обмінялись один з одним фотокарткми. Скільки всього фотокарток було роздано?

Задача 3.

     Скільки різних перестановок можна утворити із букв слова «задача»?

VІІ. Правило суми і правило добутку.

       Комбінаторні задачі бувають різних видів. Але більшість із них розв’язують за допомогою двох основних правил: правила суми і правила добутку.

                                              Правило суми.

Якщо елемент  а  можна вибрати  mспособами, а  елемент   b  – n  способами,   то  вибір   “ a  або b “  можна  здійснити   m + n способами  – правило  суми .

Наприклад,  якщо на  столі лежать  8  яблук  і  3 груші,     то  один  із фруктів  можна  вибрати   8 + 3 = 11 способами .

 

Задача 1. У ящику лежить 12 білих і 8 чорних пронумерованих кульок. Скількома способами можна вибрати з ящика три кульки одного кольору?

Розв’язання. Три кульки білого кольору можна вибрати                                       = = 220 способами.

Три кульки чорного кольору можна вибрати

= 56 способами.

За правилом суми або три білих, або три    чорних кульки можна вибрати

  + = 220 + 56 = 276 способами.

 

Правило добутку.

 

       Якщо елемент  а   можна вибрати   b способами ,  а  після цього елемент  b  можна вибрати  n  способами, то вибір  “ a  і  b “  можна  здійснити  m · n способами – правило  добутку.

        Наприклад, якщо на столі лежать 8  яблук  і 3  груші, то вибрати пару  фруктів  -  яблуко  і  грушу  можна  8 · 3 = 24 способами.

Задача 2. Збори з 29 осіб обирають голову, секретаря та трьох членів комісії. Скількома способами це можна зробити?

Розв’язання. Голова та секретар мають різні обов’язки, тому їх можна обрати             = способами  

Члени комісії мають однакові обов’язки, тому їх можна обрати

= способами.

Тоді за правилом добутку голову, секретаря і трьох членів комісії можна обрати

  812 = 2375100 способами.

 

VІІІ. Приклади розв’язування задач.

Приклад 1.

     Скільки різних прямих можна провести через 10 точок площини, з яких жодні три не лежать на одній прямій?

 

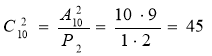
Приклад 2. Скільки можна утворити різних трицифрових додатних цілих чисел у десятковій системі числення, не повторюючи цифри у запису числа?

 

Розв'язання

Із 10 цифр можна утворити = 10 ∙ 9 ∙ 8 = 720 різних трицифрових чисел. З них із цифри 0 починаються   = 9 ∙ 8 = 72 числа. Усього чисел, що відповідають умові, можна утворити – = 648.

Відповідь: 648 чисел.

 

Приклад 3. Відомо, що старосту і його заступника в класі можна вибрати шістьмастами різними способами. Скільки учнів у класі?

Розв'язання

Позначимо кількість учнів у класі через де, (х — натуральне число). Шукана підмножина є впорядкованою, тому можна записати:

= 600.

х(х – 1) = 600;

х² – х – 600 = 0;

х₁= 25 , х₂ = -24.

- 24 не відповідає умові задачі.

Відповідь: 25 учнів.

Приклад 4. Розв'язати рівняння = х Р_х-2.

Розв'язання

Використаємо формулу (3)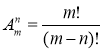 

х – (х – 3) = 3,  х >2, х N.

;

(х–2)!(х– 1)х = 6х(х–2)!;

(х–2)!(х– 1)х–6х(х–2)! = 0;

(х–2)!х(х–1–6)=0;

(х–2)!≠0,х≠0,х–7= 0,

х = 7.

Відповідь: х =7.

 

Приклад 5. Скількома способами можна розподілити уроки в шести класах між трьома вчителями, якщо кожний учитель викладатиме у двох класах?

 

Розв'язання.

 

Перший учитель може вибрати два класи з шести різними способами. Після вибору першого вчителя другий може вибрати два класи з чотирьох, що залишилися,  різними способами. Тоді за правилом добутку два вчителі можуть вибрати по два класи ∙різними способами. Якщо вони вже зробили вибір, то третій може взяти лише ті два класи, що залишилися. Тому шукана кількість способів дорівнює

.

Відповідь: 90 способами.

Приклад 6. У класі 18 учнів. Відомо, що скласти групу чергових учнів з двох хлопців і двох дівчат можна 1260 способами. Скільки в класі хлопців і скільки дівчат?

Розв'язання.

Нехай у класі х хлопців (хN, 2 ≤  х ≤ 16), тоді дівчат 18 – х. За правилом добутку складаємо рівняння: .

, ,

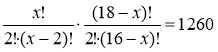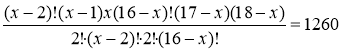х(х–1)(17 – х)(18 – х)= 5040.

Нехай х=t + 9, -7 ≤  t ≤ 7,tZ.

(t + 9)(t+ 8)(8 – t)(9 – t)= 5040,

(81–t²)(64–t²) = 5040,

t⁴–145t ² +144 = 0,

t²=144, або t² =1.

Звідси t = -1, тоді х =10, або t = 1, тоді х = 8.

Значення t= ± 12 не відповідають умові заміни.

Відповідь: У класі 10 дівчат, 8 хлопців, або 8 дівчат, 10 хлопців.

 

 

ІХ. Підведення підсумку заняття. Домашнє завдання.

Розділ 3,  § 12, 13.                    

Розв’язати задачі.

1. Для проведення іспиту створюється комісія з двох викладачів. Скільки різних комісій можна скласти з п’яти викладачів?

2.     Скількома способами можна сформувати поїзд з 8 вагонів?

3. Скількома способами можна вибрати 4 яблука із 10?

4. Скількома способами можна розподілити 3 різних путівки між 25 студентами?

5. Із семи бігунів і трьох стрибунів треба скласти команду із п’яти чоловік, в яку б входив хоч би один стрибун. Скількома способами це можна зробити?

6. Розв'язати рівняння .