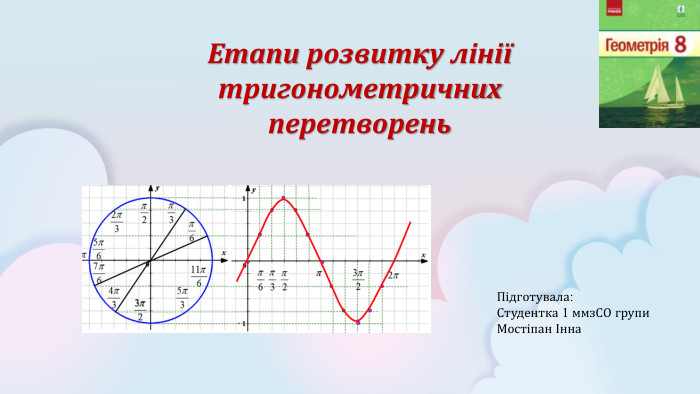
Етапи розвитку лінії тригонометричних перетворень

Етапи розвитку лінії тригонометричних перетворень. Підготувала: Студентка 1 ммз. СО групи. Мостіпан Інна

Тригонометрія — слово грецьке і в буквальному перекладі означає вимірювання трикутників (τρίγονο — трикутник, а μετρειν — виміряю).Історія походження «тригонометрії»Потреба у вимірюванні відстаней і кутів виникла ще у стародавні часи через необхідність визначення положення зірок на небі, кораблів у відкритому морі, караванів у пустелі тощо. Деякі знання з тригонометрії накопичили і вчені Стародавнього Вавилону. Засновниками тригонометрії прийнято вважати давньогрецьких вчених Гіпарха (бл. 180 р. – бл. 125 р. до н.е.) і Птолемея ( бл. 100 р. – бл. 178 р.). Зокрема Гіпарх склав таблиці хорд – перші тригонометричні таблиці. Більш точні таблиці синусів склав Птолемей. Крім цих таблиць, його праця «Альмагест» містила також тогочасні відомості з астрономії та суміжних наук. У Європі вперше тригонометрія, як самостійна наука, трактується у праці «П’ять книг про трикутник усіх видів» Йоганна Мюллера (1436 – 1476). Подальший розвиток тригонометрії відбувся завдяки Миколаю Копернику (1473 – 1543), Франсуа Вієту (1540 – 1603), Йоганну Кеплеру (1571 – 1630) і був пов’язаний з дослідженнями в астрономії. Гіпарх. Птолемей. Йоганн Мюллер. Миколай Коперник. Йоганн Кеплер. Франсуа Вієт

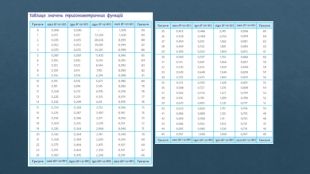
Сучасного вигляду тригонометрія набула у працях Леонарда Ейлера (1707 – 1783), який уперше сформулював означення тригонометричних функцій, розглянув їх для довільних кутів та довів кілька тригонометричних формул. Термін «синус» уперше з’явився у працях індійського вченого Аріабхатти (476 – 550). Термін «косинус» є скороченням латинського “complementy sinus”, тобто додатковий синус. Сучасні позначення “sin x” i “cos x” уперше запропонував Йоганн Бернуллі в 1739 р. в листі до Леонарда Ейлера. Ейлер їх прийняв і систематизував. Терміни «тангенс» і «котангенс» уведено арабським математиком Абу-н-Вефа (940 – 998). Він же склав перші таблиці тангенсів і котангенсів. Леонардо Ейлер. Йоганн Бернуллі

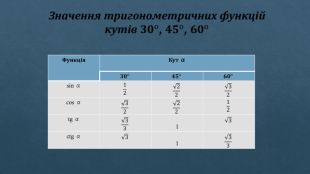
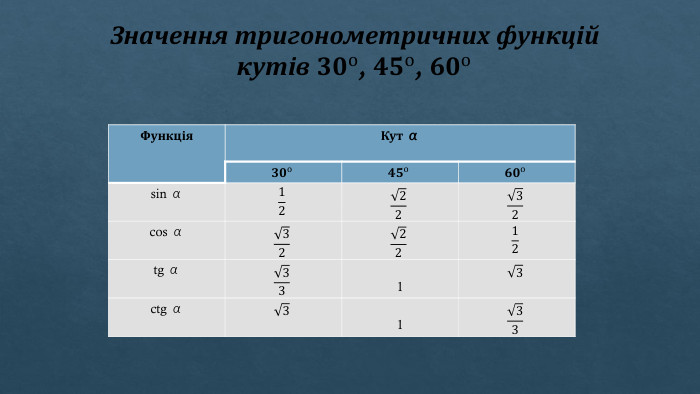
Етапи вивчення теми у шкільному курсі математики. Перше знайомство з тригонометричними функціями кутового аргументу в геометрії. Значення аргументу розглядається в проміжку (0о;90о). На цьому етапі учні дізнаються, що sin, сos, tg і ctg кута залежать від його градусної міри, знайомляться з табличними значеннями, основною тригонометричною тотожністю і деякими формулами. Узагальнення понять синуса, косинуса, тангенса і котангенса для кутів (0о; 180о). На цьому етапі розглядається взаємозв'язок тригонометричних функцій і координат точки на площині, доводяться теореми синусів і косинусів, розглядається питання рішення трикутників за допомогою тригонометричних співвідношень.  Введення понять тригонометричних функцій числового аргументу. Систематизація і розширення знань про тригонометричні функції числа, розгляд графіків функцій, проведення дослідження, в тому числі і з допомогою похідної

Відмітимо, що існує декілька способів визначення тригонометричних функцій. Їх можна поділити на дві групи: аналітичні і геометричні. До геометричних способів відносять визначення тригонометричних функцій на основі проекцій і координат радіус-вектора, визначення через співвідношення сторін прямокутного трикутника і визначення за допомогою числового кола. У шкільному курсі перевага віддається геометричним способам внаслідок їх простоти і наглядності. Відмітимо, що вивчення тригонометричних функцій в шкільному курсі має деякі особливості. По-перше, до вивчення тригонометричних функцій, розглядалися функції виду у=f(х), де х і у- деякі дійсні числа, саме тут - куту у відповідність ставиться число, що є декілька незвичним для учнів. Крім того, раніше всі функції задавалися формулами, в яких явно було вказано порядок дій над значеннями аргументу для отримання значень функції. Тепер же учні стикаються з функціями, заданими таблицею. Таким чином, вивчаючи тригонометричні функції, учні краще починають розбиратися в суті самого поняття функції. Вони починають усвідомлювати, що функцією може бути залежність між будь-якими множинами об'єктів, навіть якщо вони мають різну природу (лише б кожному значенню аргументу відповідало єдине значення функції).

Тригонометричні функції гострого кута. Синусом гострого кута α прямокутного трикутника (позначається sin α) називається відношення протилежного катета до гіпотенузи:sin α = ас  Косинусом гострого кута α прямокутного трикутника (позначається cos α) називається відношення прилеглого катета до гіпотенузи:cos α = 𝑏𝑐  Тангенсом гострого кута α прямокутного трикутника (позначається tg α) називається відношення протилежного катета до прилеглого:tg α = а𝑏 Котангенсом гострого кута α прямокутного трикутника (позначається сtg α) називається відношення прилеглого катета до протилежного:сtg α = 𝑏𝑎 

Тригонометричні тотожностіТеорема (основна тригонометрична тотожність)Для будь-якого гострого кута α 𝒔𝒊𝒏𝟐α + 𝒄𝒐𝒔𝟐α = 1 Наслідок. Для будь-якого гострого кута αsinα = 1−𝑐𝑜𝑠2αcos α= 1−𝑠𝑖𝑛2αtg α = 𝑠𝑖𝑛α𝑐𝑜𝑠αctg α = 𝑐𝑜𝑠α𝑠𝑖𝑛α tg α * ctg α = 1  Теорема (формули доповнення)Для будь-якого гострого кута αsin (90𝑜 - α) = cos αcos (90𝑜 - α) = sin α Наслідок. Для будь-якого гострого кутаαtg (90𝑜 - α) = ctg αctg (90𝑜 - α) = tg α 

Значення тригонометричних функційкутів 𝟑𝟎о, 𝟒𝟓о, 𝟔𝟎о {5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}Функція. Кут α𝟑𝟎о𝟒𝟓о𝟔𝟎оsin α122232cos α322212tg α3313ctg α3133{5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}Функція. Кут αsin αcos αtg α1ctg α1

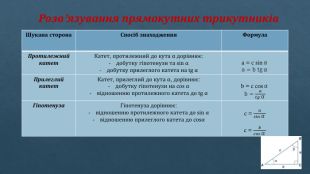
Розв’язування прямокутних трикутників{5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}Шукана сторона. Спосіб знаходження. Формула. Протилежний катет. Катет, протилежний до кута α дорівнює:добутку гіпотенузи та sin αдобутку прилеглого катета на tg αa = c sinαa = b tgα Прилеглий катет. Катет, прилеглий до кута α, дорівнює:добутку гіпотенузи на cos αвідношенню протилежного катета до tg αb = c cosαb = 𝑎𝑡𝑔αГіпотенуза. Гіпотенуза дорівнює:відношенню протилежного катета до sin αвідношенню прилеглого катета до cosαc = 𝑎𝑠𝑖𝑛αc = 𝑏𝑐𝑜𝑠α{5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}Шукана сторона. Спосіб знаходження. Формула. Протилежний катет. Катет, протилежний до кута α дорівнює:добутку гіпотенузи та sin αдобутку прилеглого катета на tg αa = c sinαa = b tgα Прилеглий катет. Катет, прилеглий до кута α, дорівнює:добутку гіпотенузи на cos αвідношенню протилежного катета до tg αГіпотенуза. Гіпотенуза дорівнює:відношенню протилежного катета до sin αвідношенню прилеглого катета до cosα

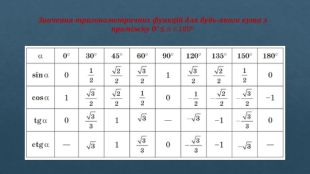
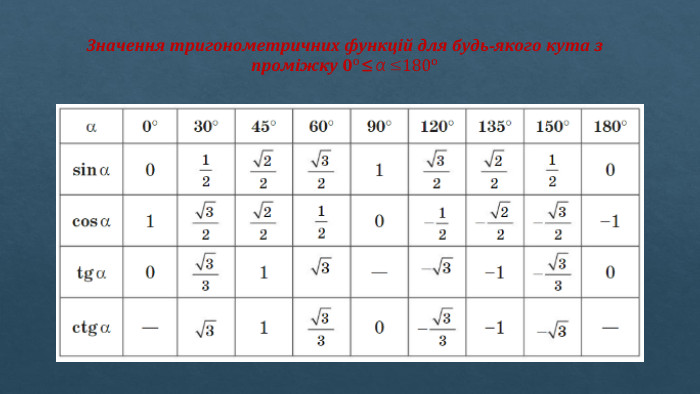
Тригонометричні функції кутів від 𝟎о до 𝟏𝟖𝟎о. Означення тригонометричних функцій на колі Коло радіусом 1 з центром у початку координат називають тригонометричним. В тригонометричному колі синус і косинус гострого кута дорівнюють відповідно ординаті і абсцисі точки, в якій сторона даного кута перетинає коло, а тангенс і котангенс цього кута дорівнюють відношенням ординати до абсциси й абсциси до ординати відповідно: sinα = y , cosα = x, tgα = 𝑦𝑥, ctgα = 𝑥𝑦 Зазначимо, що значення тригонометричних функцій залежать лише від градусної міри кута. Використаємо отримані рівності для означення тригонометричних функцій будь-якого кута від 0о до 180о 

Означення. Для будь-якого кута αз проміжку 0о≤α≤1800 sinα=y, cosα=x, tgα=𝑦𝑥 (α≠90𝑜), ctgα=𝑥𝑦 (α≠0𝑜, α≠180𝑜), де х, у – координати відповідної точки М тригонометричного кола (мал.)  Косинуси, тангенси й котангенси тупих кутів є від’ємними числами. Якщо косинус, тангенс та котангенс кута α (α<180о) від’ємні, то кут α тупий 

Тригонометричні тотожності для будь-якого кута α з проміжку 𝟎о≤α≤180о 𝑠𝑖𝑛2α + 𝑐𝑜𝑠2α=1tgα=𝑠𝑖𝑛α𝑐𝑜𝑠α (α≠90𝑜)ctgα =𝑐𝑜𝑠α𝑠𝑖𝑛α(0о<α<1800)tg α* ctg α=1 (α≠0𝑜, α≠90𝑜, α≠180𝑜) 

Теорема. Для будь-якого кута αз проміжку 0о≤α≤1800 sin(180𝑜- α)=sin αcos (180𝑜- α)= - cos α  Наслідокtg(180𝑜- α)= - tg α (0о≤α≤1800, α≠90𝑜)ctg(180𝑜-α)= - ctgα (0𝑜<α<180𝑜) 

Значення тригонометричних функцій для будь-якого кута з проміжку 𝟎о≤α≤180о 

Теорема косинусів. Квадрат сторони трикутника дорівнює сумі квадратів двох інших сторін мінус подвоєний добуток цих сторін і косинуса кута між ними. ВС2=АВ2+АС2-2*АВ*АС*cos. А Наслідок з теореми косинусів. Нехай a, b, c – довжини сторін трикутника, причому a – довжина його найбільшої сторони. Якщо а2< 𝑏2+𝑐2, то трикутник є гострокутним. Якщо а2> 𝑏2+𝑐2, то трикутник є тупокутним. Якщо а2=𝑏2+𝑐2, то трикутник є прямокутним. 

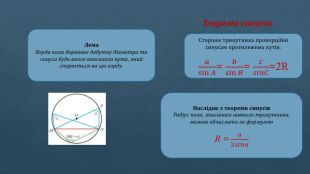
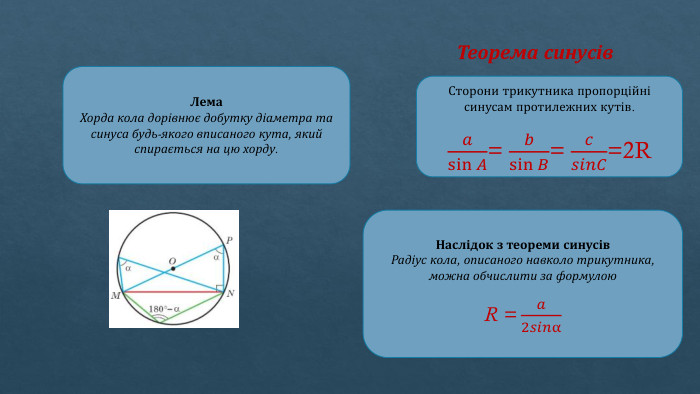
Теорема синусів. Лема. Хорда кола дорівнює добутку діаметра та синуса будь-якого вписаного кута, який спирається на цю хорду. Сторони трикутника пропорційні синусам протилежних кутів.𝑎sin𝐴= 𝑏sin𝐵= 𝑐𝑠𝑖𝑛𝐶=2 R Наслідок з теореми синусів. Радіус кола, описаного навколо трикутника, можна обчислити за формулою. R = 𝑎2𝑠𝑖𝑛α 

Список використаних джерел. Геометрія: підруч. для 8 кл. закл. загал. серед. освіти/[А. П. Єршова, В. В. Голобородько, О. Ф. Крижановський, С. В. Єршов.] – 2-ге вид., перероб. – Харків.: Вид-во «Ранок»,2021. – 256с. Геометрія: підруч. для 9 кл. закл. загал. серед. освіти/[А. П. Єршова, В. В. Голобородько, О. Ф. Крижановський, С. В. Єршов.]. – Харків.: Вид-во «Ранок», 2017. – 256с. Геометрія: підруч. для 9 кл. загальноосвіт. навч. закладів / А. Г. Мерзляк, В. Б. Полонський, М. С. Якір. – Х. : Гімназія, 2017. – 240с.

Дякую за увагу!!!