Етапи уроку критичного мислення
ЕТАПИ УРОКУ КРИТИЧНОГО МИСЛЕННЯ
- Етап розминки
Розминка ( замінює так звані організаційні етапи класичного уроку ). Головна функція – створити сприятливий психологічний клімат на уроці.
Актуальність етапу – теплий психологічний клімат сприяє:
- кращому засвоєнню навчального матеріалу;
- підвищенню авторитету вчителя;
- психологічному розвантаженню учнів, які за день мають 6-7 різних уроків.
Фрагмент уроку у 5-ому класі
… Знову ми зібралися на уроці математики. Давайте, створимо позитиву ауру в класі: посміхнемося один одному. Народна мудрість каже: «Мудрим ніхто не вродився, а …». Запропонуйте свій варіант закінчення прислів’я. (Виконання завдання).
Народна мудрість стверджує: «Мудрим ніхто не вродився, а навчився». А я вам бажаю, щоб урок пройшов цікаво і з користю, щоб скарбничка ваших знань поповнилася.
Етап передбачає:
- постановку мети уроку;
- розвиток внутрішньої мотивації до вивчення конкретної теми та предмета загалом.
Актуальність етапу – навчальний матеріал засвоюється краще, якщо:
- учні розуміють його конкретну практичну значущість для кожного з них;
- чітко знають, чого від них вимагатимуть на уроці.
На етапі обґрунтування навчання часто проводжу графічні диктанти (геометрія 10 кл. «Зображення фігур у стереометрії»):
Чи може паралельна проекція паралелограма бути :
- квадратом ;
- трапецією ;
- чотирикутником зі сторонами 4см, 5см, 6см і 7см ;
- чотирикутником з кутами 30°, 150°, 30°, 150°?
Трикутник А´В´С´- паралельна проекція трикутника АВС. Чи правильно, що :
- висоти трикутника А´В´С´- проекції висот трикутника АВС;
- медіани трикутника А´В´С´- є медіанами трикутника АВС?
Ключ-відповідь до графічного диктанту
● ▲ ▲ ● ▲ ●, де ● – так, ▲ – ні
1 2 3 4 5 6
Ефективними є вправи на знаходження раціонального способу розв’язання:
- Знайти суму:
27·68 + 32·27;
1+3+5+…+148+150.
- Якою цифрою закінчується значення виразів:
![]() ;
;
![]() +
+ ![]() .
.
- Назвіть три останні цифри добутку:
1·2·3·…·16·17.
Проблемні запитання та завдання спонукають учнів критично ставитися до об’єму своїх знань і усвідомлювати необхідність їх поповнення.
Наведу приклади таких запитань:
- Чи може бути твірна конуса рівна радіусу основи? (11 кл. Ні, бо гіпотенуза завжди більша від катета);
- Чи існує призма, яка має 16 ребер? 160 ребер? 1600 ребер? (11 кл. Не існує, бо в кожній вершині призми сходяться 3 ребра. Отже, їх кількість повинна бути кратною трьом) ;
- Чому стілець на чотирьох ніжках може хилитатися, а на трьох – ні? (10 кл. Тому що через 3 точки, що не лежать на одній прямій, проходить єдина площина).
-
Чи вистачить 1 самовара чаю , якщо гості Мухи-Цокотухи випили
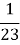 ,
, 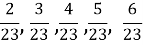 частини ? (5 кл.)
частини ? (5 кл.)
-
Як зручно обчислити:
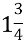 +2
+2 + 3
+ 3  + 6
+ 6  +7
+7  + 8
+ 8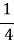 ? (5 кл.)
? (5 кл.)
- Скільки дроту треба для виготовлення моделі прямокутного паралелепіпеда? (5 кл.)

![]()
![]()
![]()
- Чи можна провести змагання з плавання в басейні розмірами 20м ×50 м, якщо його заповнити 100 л води? (5 кл.)
Девіз етапу: «Пробудіть, викличте зацікавленість, схвилюйте, спровокуйте учнів пригадати те, що вони знають».
На цьому етапі відтворюють знання, вміння, потрібні для наступних етапів уроку, встановлюють рівень досягнень з теми.
Актуальність етапу – оскільки знання, пов’язані з досвідом учня, запам’ятовуються краще та швидше, то створюються умови для «відкриття», самостійного добування знань, і за цих умов підвищується роль учня на уроці.
На етапі актуалізації доцільно проводити наступні ігри:
- «Знайди помилку» (8 кл. «Раціональні вирази. Скорочення дробів»):
-
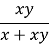 =
=  ;
;
-
 =
= 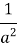 ;
;
-
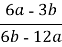 =
= 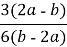 =
=  .
.
- «Вірю, не вірю», яка проводиться за допомогою сигнальних карток: ▲, ● (10 кл. «Паралельне проектування і його властивості»):
- Через довільну точку простору можна провести лише одну пряму, паралельну даній прямій (За бажанням учителя учні коментують свої відповіді).
- Якщо дві прямі у просторі не перетинаються, то вони паралельні.
- Якщо площина перетинає одну з двох паралельних прямих, то вона перетинає і другу.
- Якщо пряма паралельна деякій площині, то вона паралельна до будь-якої прямої цієї площини.
- Якщо дві прямі паралельні площині, то вони паралельні одна одній.
Ефективними і цікавими для учнів є нетипові повідомлення, що спонукають до критичного мислення (геометрія 11 кл.) : «В одній із рекламних газет було надруковане таке повідомлення: «Ви, напевно, чули про незвичайні властивості чотиригранної піраміди, яка цілюще діє на людину. Є дані, що на відміну від чотиригранної, тригранна генерує шкідливу енергію». Де тут помилка, яка не потребує перевірки, а лише елементарних знань з основ стереометрії?» (Тригранної піраміди не існує).
Ще одна життєва ситуація (9 кл. «Сума геометричної прогресії»):
Задача. Одного разу незнайомець постукав у двері багатого купця і запропонував йому таку угоду: «Я буду щоденно приносити тобі по 100000 грн. упродовж 30 днів, а ти мені першого дня даси 1 коп., другого – 2 коп., і так щодня будеш збільшувати попереднє число у 2 рази. Якщо тобі вигідно, то завтра ж почнемо.» Хто виграв у цій справі?
Доцільною є робота в парах у вигляді гри «Двоє як один» та гри «Один за всіх» (ланцюжок). Наприклад (6 кл. «Додавання і віднімання звичайних дробів»):
-
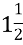 +
+ 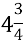 = …
= …
-
… − 5
 = …
= …
-
… +
 = …
= …
-
… −
 = …
= …
-
… −
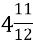 = …
= …
-
… −
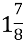 = …
= …
-
… +
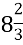 = …
= …
-
… +
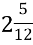 = …
= …
-
… +
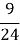 = …
= …
(Відповідь: 12).
На цьому етапі учень ознайомлюється з новою інформацією, аналізує, визначає особисте її розуміння, вчитель має найменший вплив на учня.
Актуальність етапу – етап передбачає розвиток уміння:
- працювати з інформацією;
- працювати самостійно;
- виділяти головне, суттєве;
- формування компетентності учня з предмета.
На етапі усвідомлення змісту часто пропоную виконати завдання на встановлення відповідності та прокоментувати свій вибір. Наприклад: алгебра 10кл. «Розв’язування ірраціональних рівнянь».
Умова: Відповідь:
-
 А)
А) 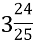 ; 2
; 2
-
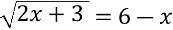 Б) 3; 1,5
Б) 3; 1,5
-
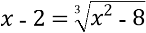 В) -3; 1,5
В) -3; 1,5
-
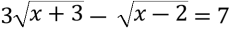 Г) 3 ; Д) 11; 3
Г) 3 ; Д) 11; 3
-
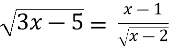 Е) 0; 3; 4 ; Є) 6; -6
Е) 0; 3; 4 ; Є) 6; -6
-
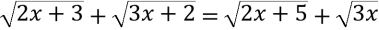 Ж)
Ж) 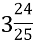
З) 6
Правильні відповіді:1 – Є; 2 – Г; 3 – Е; 4 – З; 5 –Г; 6 – Г.
Корисною для розвитку критичного мислення є також гра «На помилках вчимося» (знайти помилку чи недолік): геометрія 9 кл. «Декартові координати на площині».
Знайдіть помилку чи недолік.
-
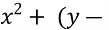 2) 2 = 1
2) 2 = 1 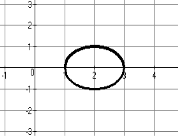
-
( x – 3)2 + y2 = 2

-
x2 + y2 = 25
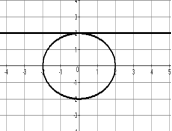
-
x2 + y2 = 4
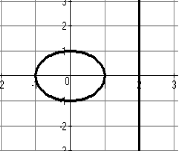
-
(x−2)2 + (y+4)2 = 4
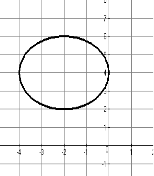
На цьому етапі :
- Учень стає власником ідеї, інформації, знань;
- Можливість використання знань;
- Обмін знаннями з іншими учнями;
- Оцінка та самооцінка діяльності.
Актуальність етапу:
- усвідомлення того, що було зроблено на уроці;
- демонстрування знань і того, як можна їх застосовувати;
- можливість замислитись над підвищенням якості роботи;
- можливість диференціювати домашнє завдання;
- визначення необхідності корекції.
 На етапі рефлексії ефективним прийомом розвитку критичного мислення є створення навмисної помилки:
На етапі рефлексії ефективним прийомом розвитку критичного мислення є створення навмисної помилки:
 В С
В С
![]() а D
а D
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Критичний аналіз умови задачі (7 кл. «Трикутники»):
Знайти периметр рівнобедреного трикутника, якщо довжини його сторін 3 см і 10 см.
Вправа «Яка з фігур зайва»
- 5 кл. «Кут. Величини кута»
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
5 кл. «Площі за об’єми геометричних фігур»




![]()
![]()
![]()
![]()



![]()
![]()
![]()
![]()

![]()
![]()

![]()
![]()

![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()


про публікацію авторської розробки
Додати розробку