Формула Герона для площі трикутника.

УРОК № ____

Тема уроку.  Формула Герона для площі трикутника.

Мета уроку: навчити учнів знаходити площу трикутника за трьома сторонами.

Тип уроку:  формування та вдосконалення знань.

Хід уроку

І. Перевірка домашнього завдання й актуалізація знань учнів

Учні самостійно повторюють, які формули для обчислення площі трикутника були одержані на попередньому уроці.

Потім класу пропонується самостійна робота.

На дошці заздалегідь заготовлено рисунки до задач. Величини даних елементів (відрізків, кутів) учитель записує в ході читання умов задач. Учні під час оформлення розв'язання не виконують ри­сунків у зошитах (на аркушах). У дужках наведено дані для другого варіанта.

Самостійна робота

Задача 1. У трикутнику катет а дорівнює 3 (b = 4) гіпотенуза с дорівнює 5. Знайдіть площу трикутника.

Задача 2. У трикутнику дві сторони дорівнюють 5 і 6 см (4 і 7 см), а кут між ними — 60° (45°). Знайдіть площу трикутника.

Задача 3. Знайдіть площу рівностороннього трикутника, якщо його сторона дорівнює 4 см (8 см).

Задача 4. У трикутнику зі сторонами 4 і 12 см (6 і 10 см) до цих сторін проведено висоти; менша з них дорівнює 8 см (4 см). Чому дорівнює більша висота?

II. Вивчення нового матеріалу

Формулу для знаходження площі трикутника за трьома сторо­нами дістав давньогрецький учений Герон Александрійський, який жив у І ст. н. є.

На дошці записується умова задачі № 29 § 14 і пропонується на­мітити план розв'язання.

Д а н о: а, b, с — сторони ∆АВС .Знайти: S_ABC.

Доцільно розглянути кілька способів розв'язання задачі.

Спосіб 1.

1. За теоремою косинусів знаходимо cosC .
2. З рівності sin²C + cos²C = l знаходимо sinC .
3. За формулою S_ABC = 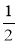absinC знаходимо площу трикутника.

Спосіб 2.

1. Проводимо висоту до сторони а. З рівняння b² – х² = с² – (а – х)² знаходимо х — довжину одного з відрізків сторони а.
2. За теоремою Піфагора знаходимо висоту, проведену до сторони а.
3. За формулою S = 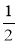ah_a знаходимо площу трикутника.

Учитель пропонує учням прокоментувати розв'язання цієї задачі, наведене в підручнику (п. 125).

1. Маємо S = 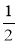ab sinγ (рис. 91).
2. За теоремою косинусів с² = а² + b² – 2ab cos γ. Звідси .
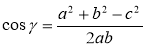3. sin²γ = 1 – cos²γ = 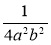(c – a + b)(c + a – b)(a + b – c)(a + b + c).
4. Беручи до уваги, що a + b + c = 2p, a + b – c =2p – 2c, а + с – b = 2р – 2b, с – а + b = 2р – 2а, де р — півпериметр трикут­ника, дістаємо: .
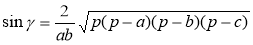5. S = 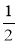a b sin γ = .

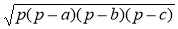Висновок: .

Зауваження. Перехід від пункту 3 до пункту 5, тобто до виразу

, можна записати окремо на дошці за підручником, а формулу Герона дістати, помноживши обидві частини останньої рівності на a b.

III. Закріплення нових знань і вмінь учнів

Розв'язування задач

Задачу № 30 (1) § 14 учитель розв'язує на дошці.

Розв'язання

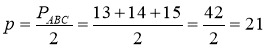1. ; р - а = 21 – 13 = 8; р – b = 21-14 = 7, р – с = 21 – 15 = 6.
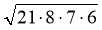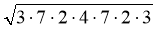2. S_ABC = = = 84.

Відповідь. 84.

Задача №30 (2) §14

Розв'язання

1. р = 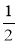(5 + 5 + 6) = 8, p - a = 3, p – b = 2, р – с = 3.
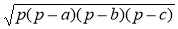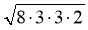2. S_ABC = = = 12.

Відповідь. 12.

Задача 1. Знайдіть найменшу висоту трикутника зі сторона­ми 4, 5, 7.

Розв'язання

1. S = 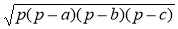.  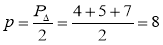, р - а = 8 – 4 = 4;              p – b = 8 – 5 = 3, p – c = 8 – 7 = 1. S = 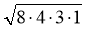= 4.
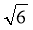2. Оскільки сторони в трикутнику обернено пропорційні його ви­сотам (задача № 20 § 14), то найменшу висоту проведено до най­
   більшої сторони. S =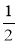 7 ∙ h_c, .

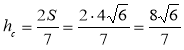Відповідь. .

Задача 2. Знайдіть найбільшу висоту трикутника зі сторона­ми 3, 5, 6.

Розв'язання

1. S = 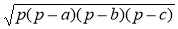= = 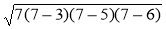2.
2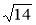. Найбільшій висоті відповідає найменша сторона.

Отже, S = ∙3∙h,  2= h, h = .

Відповідь. .

IV. Завдання додому

Задачі № 30 (3), 32 (1), 33, 36 (1, 3) § 14.