Коло та його елементи.
ГЕОМЕТРИЧНІ ПОБУДОВИ
УРОК _____
Тема. Коло.
Мета: ознайомити учнів з поняттям кола та його елементів, властивістю діаметра, що проходить через середину хорди; розвивати логічне мислення учнів.
Обладнання: циркуль, лінійка, посібник «Усні вправи з геометрії» для 7—11 класів» під ред. А.С.Раухмана, кодоскоп.
ХІД УРОКУ
І. Організаційний момент.
ІІ. Мотивація діяльності учнів, повідомлення теми і мети уроку.
- Пригадати завдання старого Хоттабича з однойменного фільму-казки: «Намалювати лінію без початку і без кінця». Як юний маг вийшов з положення? (Намалював коло.)
- Арена цирку, кратер вулкана, спортивний диск, колесо, обруч ... Що спільного у перелічених об'єктів? (їх форма.)
- Де ще зустрічаються фігури (або їх частини), що мають форму кола або круга?
- Зробити висновок про необхідність вивчення властивостей такої лінії, як коло.
III. Вивчення нового матеріалу.
- Сформулювати означення кола.
Коло — це фігура, що складається з усіх точок площини, рівновіддалених від даної точки (центра кола).
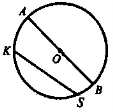
О — центр, КS — хорда, АВ — діаметр, ОА = ОВ — радіус; d = 2R, де R — радіус; d — діаметр.
- Усно розв'язати вправи (малюнки наперед виконано на дошці або проектуються за допомогою кодоскопа).
а) «Прикладами хорд кола є діаметри і радіуси». Чи правильне таке твердження? Пояснити.
б) Чи може хорда бути у три рази більшою за радіус того самого кола?
в) На колі взято точку. Скільки діаметрів і скільки хорд можна провести через цю точку?
|
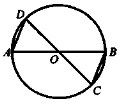
г) Дано: коло, О — центр кола. Довести: AD || ВС, AD = BC. |
|
|
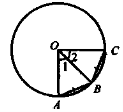
ґ) Дано: коло, О — центр кола, АВ = ВС.
Довести: |
|
IV. Формування вмінь застосовувати вивчений матеріал.
Сформулювати і довести твердження про властивість діаметра, що проходить через сере дину хорди.
Запропонувати учням прочитати з підручника [1] умову задачі № 4 (§ 5), показати, що це є твердження, обернене до доведеного; запропонувати задачу № 4 (§ 5) для домашнього розв'язування. (Тут і далі номери задач вказано за підручником [1].
|
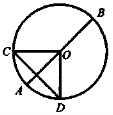
Задача № 4. Дано: коло, О — центр кола, АВ — діаметр, CD — хорда, К — середина CD.
Довести: АВ |
|
|
Розв'язання У трикутнику COD: ОС = OD (як радіуси), СК = KD (за умовою). Отже, ∆CОD — рівнобедрений. Тому ОК — медіана, бісектриса і висота трикутника COD.
Отже, АВ |
|
|
|
|
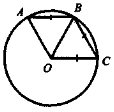
Дано: коло, О — центр кола, АВ, ВС — хорди, АВ = ВС = ОС.
Знайти: |
|
|
Розв'язання ОА = ОВ = ОС (як радіуси).
Отже, трикутник АОВ — рівносторонній, тому Аналогічно буде рівностороннім трикутник ВОС (ОВ = ВС = CO),
тому Відповідь. 120°. |
|
V. Підсумок уроку.
VI. Домашнє завдання.
За підручником [1]: § 5, п. 38, № 2, 4, 5 (1).
1


про публікацію авторської розробки
Додати розробку