Формула коренів квадратного рівняння

Тема. Формула коренів квадратного рівняння

Мета: домогтися засвоєння учнями змісту поняття «дискримінант квадратного рівняння», формули дискримінанта та схеми виводу фор­мул для розв'язування квадратного рівняння загального вигляду, а та­кож формул коренів квадратного рівняння; сформувати первинні вміння знаходити за формулами дискримінант квадратного рівняння, за його значенням визначати кількість розв'язків квадратного рівнян­ня й обчислювати корені квадратного рівняння.

Тип уроку: засвоєння знань та вмінь.

Наочність та обладнання: опорний конспект «Квадратні рівняння».

Хід уроку

I. Організаційний етап

II. Перевірка домашнього завдання

Самостійна робота 10

III. Формулювання мсти і завдань уроку

З метою створення відповідної мотивації пропонуємо учням розв'я­зати низку рівнянь: кілька з них — неповні квадратні рівняння, а інші — квадратні рівняння загального вигляду, причому два з них такі, що по­вний квадрат виділяється легко (наприклад, зведені квадратні рівняння з парними другими коефіцієнтами), а два такі, що виділення повного квадрата ускладнене (квадратні рівняння, що не є зведеними). Аналіз ситуації, що склалась, приводить до формулювання проблеми: не­обхідно знайти єдиний достатньо простий алгоритм розв'язання квад­ратних рівнянь загального вигляду. Розв'язання цієї проблеми і є голов­ною метою уроку.

IV. Актуалізація опорних знань та вмінь

 З метою успішного сприйняття учнями навчального матеріалу перед його вивченням слід активізувати такі знання і вміння учнів: прийоми виділення квадрата двочлена з даного квадрат­ного тричлена; обчислення значень змінних за формулами; розв'язування рівнянь виду х² = а.

Виконання усних вправ

1. Розв'яжіть рівняння:

а) х² = 25; б) 4х² = 1; в) 3х² = 6; г) (х – 1)² = 25; д) (х + 2)² = 0.

2. Замініть  рівняння  рівносильними   зведеними   квадратними  рів­нянням:

а) 2х² – 6х + 10 = 0; б) 3х² – 12х² + 3 = 0; в) 2х + 0,5х² – 1 = 0;

г) –х² + х – 7 = 0.

3. Подайте тричлен, якщо можливо, у вигляді квадрата двочлена:
   а) х² + 2х + 1; б) 2а + а² – 1; в) х² + 1 – 2х; г) х² + 6х + 9;

д) у² – 8у + 64; e) 36 + 12а + а²; ж) .

V. Засвоєння знань

План вивчення нового матеріалу

1. Виведення формули коренів квадратного рівняння. Схема розв'я­зання квадратного рівняння загального вигляду за формулою.
2. Приклади застосування виведеної формули.

 Виведення формули коренів квадратного рівняння загального виду традиційно здійснюється у формі розв'язування квадрат­ного рівняння загального вигляду виділенням квадрата двоч­лена. І хоча перед цим уроком було розв'язано вправи на повторення (на поновлення навичок виділення квадрата дво­члена), виведення формули може викликати певні труднощі, бо пов'язане з перетвореннями виразів з буквеними коефі­цієнтами. Тому, щоб подолати такі труднощі, перед виведен­ням формули можна ще раз показати всі перетворення на прикладі рівняння з числовими коефіцієнтами, а потім пере­ходити до роботи з буквеними виразами (або ж у випадку не­високого рівня математичних здібностей учнів подати їх у ви­гляді готових формул).

Після виведення формули важливо дати учням схему дій із застосу­вання виведених формул у вигляді алгоритму.

Розглядаючи приклади на застосування виведених формул, бажано звернутися до всіх можливих випадків (дискримінант додатний, від'єм­ний та дорівнює нулю). Під час розв'язування квадратного рівняння, дискримінант якого дорівнює нулю, слід показати два способи зна­ходження коренів (двох рівних): за виведеною формулою (яку в 9 класі будемо вивчати як формулу абсциси вершини параболи — графіка квадратичної функції у = ах² + bх + с), а також розкладанням лівої частини рівняння на множники за фор­мулою квадрата двочлена (цей спосіб стане у пригоді для побудови гра­фіка квадратичної функції шляхом геометричних перетворень графіка функції           у = х²).

VI. Формування вмінь

Виконання усних вправ

1. Знайдіть значення виразу b² – 4aс:

а) а = 1; b = 2; с = 3; б) а = 2; b = 5; с = -3.

2. Знайдіть значення виразу :

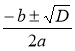а) b = -1; D = 9; а = 2; б) b = -3; D = 25; a = -2.

3. Скільки коренів має рівняння ах² + bx + c = 0, якщо значення виразу       b² – 4ас для нього дорівнює: а) 25; б) 3; в) -1; г) 0?

Виконання письмових вправ

Для реалізації дидактичної мети уроку слід розв'язати завдання та­кого змісту:

1. Знаходження дискримінанта квадратного рівняння та визначення
   кількості коренів цього рівняння.

1) Для квадратного рівняння знайдіть дискримінант і вкажіть кіль­кість його коренів:

а) 2х² – 3х + 1 = 0; б) 4х² + 4х + 1 = 0; в) -3х² + 6x – 4 = 0.

2) Обчисліть дискримінант квадратного рівняння і вкажіть число
його коренів:

а) 2х² + 3х + 1 = 0; б) 2х² + х + 2 = 0; в) 9х² + 6х + 1 = 0; г) х² + 5х – 6 = 0.

2. Розв'язування квадратного рівняння за формулою.

1) Розв'яжіть рівняння:

а) х² – 6х + 5 = 0; б) х² + 4х – 12 = 0; в) х² + 7х + 10 = 0; г) х² – 3х + 4 = 0;

д) х² – 10х + 25 = 0; є) х² – 4х – 21 = 0.

2) Розв'яжіть рівняння:

а) 2х² – 5х + 3 = 0; б) 2х² + х – 1 = 0; в) 3х² + 5х – 2 = 0; г) 4х² – 4х + 1 = 0;

д) 2х² – 3х + 2 = 0; є) 7х² – 6х – 1 = 0.

3) Розв'яжіть рівняння:

а) 3х² – 7х + 4 = 0; б) 5х² – 8х + 3 = 0; в) 3х² – 13х + 14 = 0;

г) 2у² – 9y + 10 = 0; д) 5у² – 6y + 1 = 0; є) 4х² + х – 33 = 0;

ж) у² – 10y – 24 = 0; з) р² + р – 90 = 0.

3. Не розв'язуючи квадратного рівняння, вказати ті з них, які мають задану кількість коренів.

1) Не розв'язуючи рівняння, вкажіть ті з них, які мають один корінь:

а) 9х² + 6х + 1 = 0; б) 3х² – х – 4 = 0; в) 2х² – 16х + 32 = 0.

2) Яке з рівнянь не має коренів:

а) х² + 2х – 7 = 0; б) 2х² – 3х + 8 = 0; в) 3х² + 5х + 4 = 0?

4. Розв'язування квадратного рівняння найбільш зручним способом
   (завдання передбачає повторення поняття неповного квадратного
   рівняння та способів його розв'язання в поєднанні з вивченим на
   уроці способом розв'язання квадратних рівнянь загального виду).
5. Логічні вправи та завдання підвищеного рівня складності для учнів, які мають достатній та високий рівні знань.

1) Знайдіть значення b, при яких один із коренів рівняння дорів­нює -3:

a) 20x² + bx – b² = 0; б) .

2) Доведіть, що при будь-якому значенні змінної значення виразу додатне:

а) а² + 4а + 11; б) в) т² – 4т + 51; г) .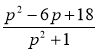

3) Вставте пропущений вираз:

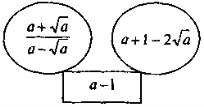
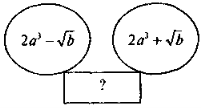
 Письмові вправи мають на меті засвоєння формул коренів квадратного рівняння (формули дискримінанта, самих коре­нів) та формування вміння застосовувати ці формули (нові знання) в поєднані з вивченими раніше способами розв'язання квадратних рівнянь (вивчений раніше матеріал). Оскільки на цьому уроці лише починається робота із закріплення знань формул коренів квадратного рівняння, з метою попередження помилок та кращого запам'ятовування вивчених формул, слід вимагати від учнів строгого дотримання алгоритму та усного й письмового відтворювання виведених формул (доцільно ви­користати такий мнемонічний прийом: запам'ятовування фор­мул у вигляді речення — «де дорівнює бе квадрат мінус чотири а це», або використовувати інші мнемонічні прийоми).

Якщо засвоєння нового матеріалу проходить успішно, то вже на цьому уроці можна запропонувати учням завдання, що передбачає по­єднання нових знань і вмінь (формул коренів квадратного рівняння та первинних умінь їх застосовувати) із набутими раніше знаннями та вмін­нями (види квадратних рівнянь та вміння визначати вид квадратного рівняння — зведене або неповне певного виду, та способів розв'язання неповних квадратних рівнянь).

VII. Підсумки уроку

В якому випадку правильно знайдено дискримінант?

а) 5х² + 3х + 2 =0, D = 49; б) 2х² – 3х – 5 = 0, D = 49;

в) (3х – 2)(3х + 2) = 6х+3, D = 49; г) 2х² – 3x + 5 = 0, D = 49.

VIII. Домашнє завдання

1. Вивчити формули коренів квадратного рівняння.
2. Розв'язати приклади на застосування цих формул.
3. На повторення: підібрати приклади завдань на перетворення ви­разів, що містять квадратні корені, розв'язування яких передбачає винесення множника з-під знака кореня, та завдання на скорочен­ня дробів.