Розробка уроку на тему "Теорема Вієта"

Тема. Теорема Вієта

Мета: домогтися засвоєння учнями змісту теореми Вієта для зведе­ного квадратного рівняння та для квадратного рівняння загального виду; сформувати вміння відтворювати вивчені твердження, викорис­товувати їх для розв'язування завдань, передбачених програмою з ма­тематики.

Тип уроку: засвоєння знань та вмінь.

Наочність та обладнання: опорний конспект «Теорема Вієта».

Хід уроку

І. Організаційний етап

II. Перевірка домашнього завдання

Самостійна робота № 11 (з корекцією)

Застосування формули коренів квадратного рівняння

III. Формулювання мсти і завдань уроку

Для створення позитивної мотивації навчальної діяльності учнів можна під час проведення самостійної роботи запропонувати учням виконати випереджальне завдання: розв'язати квадратні рівняння і для кожного з тих, що мають корені, знайти їхню суму і добуток. На етапі корекції (див. вище), перевіряючи правильність виконання завдань, слід запропонувати учням не просто порівняти свої відповіді з пра­вильними, але й порівняти отримані відповіді (суми та добутки ко­ренів) з коефіцієнтами квадратних рівнянь. Якщо учні помітять певні закономірності самі, вчителеві достатньо сформулювати проблему: не­обхідно дослідити існування загальних властивостей коренів будь-яко­го квадратного рівняння та виразити ці властивості у вигляді формул, сформувати вміння застосовувати ці властивості в розв'язуванні типових завдань.

IV. Актуалізація опорних знань та вмінь

 Для успішного сприйняття навчального матеріалу уроку слід активізувати такі знання і вміння учнів: означення квадратного рівняння, неповних квадратних рівнянь та зведених квадрат­них рівнянь, визначення коефіцієнтів квадратного рівняння, формул для розв'язування квадратних рівнянь (дискримінанта та коренів), виконання арифметичних дій з дійсними числами.

Виконання усних вправ

1. Розв'яжіть рівняння:

а) х² – 25 = 0; б) а² – 5а = 0; в) у² + 9 = 0; г) п² – 19 = 0; д) 5х² = 0,2.

2. Назвіть перший, другий коефіцієнти і вільний член квадратного
   рівняння:

а) а² + 4а – 1 = 0; б) у² – 3 = 0; в) 2b² – 5b = 0; г) 3 – 2х² – х = 0; д) 3с² = 0.

3. Знайдіть значення виразів:

; ; ; ;

; .

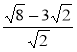V. Засвоєння знань

План вивчення нового матеріалу

1. Теорема Вієта для зведеного квадратного рівняння: формулювання і доведення.
2. Теорема Вієта для квадратного рівняння загального виду: форму­лювання і доведення:

1) теорема, обернена до теореми Вієта.

2) приклади застосування вивчених теорем.

 Формулювання і доведення теореми Вієта для зведеного квад­ратного рівняння учні зазвичай сприймають досить легко. Єдине, в чому часто помиляються, – це запис значення суми коренів квадратного рівняння: замість числа, протилежно­го другому коефіцієнту, учні часто вказують другий кое­фіцієнт. Щоб попередити ці помилки, достатньо розв'язати усні вправи.

Теорема Вієта для квадратного рівняння загального вигляду дово­диться досить легко через теорему Вієта для зведеного квадратного рівняння.

• Доведення теореми, оберненої до теореми Вієта, зазвичай не є обо­в'язковим для всіх учнів: його пропонують для самостійного опрацю­вання учням, які мають високий рівень знань та вмінь.

Останній пункт плану показує практичну значимість вивчених тео­рем: на цьому етапі вивчення матеріалу слід продемонструвати учням застосування теореми Вієта та оберненої до неї теореми для відшукан­ня коренів зведеного квадратного рівняння з цілими коефіцієнтами без обчислення дискримінанта (підбором). Коментуючи дії, що супро­воджують пошук коренів зведеного квадратного рівняння з цілими коефіцієнтами із використанням вивчених теорем, слід показати учням послідовність міркувань, яка допоможе знайти корені «методом підбору»: спочатку записати, чому дорівнює сума і добуток коренів, потім визначити, які знаки коренів (за знаком добутку). Якщо вони однакові, то модуль суми коренів дорівнює сумі модулів коренів, якщо вони різні, — модуль суми коренів дорівнює різниці модулів коренів; наприкінці розкладаємо модуль вільного члена на множники, що задовольняють попередню умову.

VI. Формування вмінь

Виконання усних вправ

1. Складіть зведене квадратне рівняння, в якому сума р і добуток q його коренів дорівнюють:

а) р = - 5; q = 4; б) р = 15; q = -6; в) р = - 5; q = 0; г) p = 0; q = -2.

2. Один із коренів квадратного рівняння х² + 4х – 21 = 0 дорівнює - 7.
   Знайдіть другий корінь.

(Розв'язати задачу різними способами.)

Виконання письмових вправ

Для реалізації дидактичної мети уроку слід розв'язати завдання та­кого змісту:

1. Чи є дані числа коренями квадратного рівняння із заданими коефіцієнтами.

Чи є дані числа коренями рівняння?

а) х² – 2,5х + 1 = 0, числа 2 і 0,5; б) х² + 20х – 125 = 0, числа -5 і 25.

2. Знаходження коренів квадратного рівняння та виконання пе­ревірки за теоремою, оберненою до теореми Вієта.

1) Знайдіть за формулою корені рівняння і виконайте перевірку за теоремою, оберненою до теореми Вієта:

а) х² – 13х + 40 = 0; б) х² + 6х + 5 = 0.

2) Розв'яжіть рівняння і виконайте перевірку за теоремою, оберне­ною до теореми Вієта:

а) х² – 2х – 9 = 0; б) 3х² – 4х – 4 = 0; в) 2х² + 7х – 6 = 0; г) 2х² + 9х + 8 = 0.

3. Знаходження суми і добутку коренів квадратного рівняння.

1) Кожне з рівнянь має корені. Знайдіть суму і добуток цих коренів:

а) 3х² – 4х + 1 = 0; б) 10х² + х – 3 = 0.

2) Знайдіть суму і добуток коренів рівняння:

а) х² – 37х + 27 = 0; б) у² + 41у – 371 = 0; в) х² – 210х = 0; г) у² – 19 = 0;

д) 2х² – 9х – 10 = 0; є) 5х² + 12х + 7 = 0; ж) -z² + z = 0; з) 3х² – 10 = 0.

4. Знаходження коренів квадратного рівняння із використанням тео­реми, оберненої до теореми Вієта.

1) Знайдіть корені рівняння за теоремою, оберненою до теореми Вієта:

а) х² – 3х + 2 = 0; б) х² – 5х + 6 = 0; в) х² + 7х + 12 = 0; г) х² + 3х + 2 = 0;

д) х² – 5х + 4 = 0; є) х² – 8х – 9 = 0; ж) х² + 4х + 3 = 0; з) х² – 2х – 3 = 0;

и) х² + 2х – 15 = 0.

2) Знайдіть підбором корені рівняння:

а) х² – 9х + 20 = 0; б) х² + 11х – 12 = 0; в) х² + х – 56 = 0; г) х² – 19х + 88 = 0.

5. Знаходження невідомого кореня та невідомого коефіцієнта квад­ратного рівняння, якщо відомий другий корінь та два коефіцієнти квадратного рівняння.

1) Знайдіть   вільний   член   q  зведеного  квадратного  рівняння
х² + px + q = 0, якщо його коренями є числа: 5; - 3; -2; -6.

2) У рівнянні х² + рх – 35 = 0 один із коренів рівняння дорівнює 7.
Знайдіть другий корінь і коефіцієнт р.

6. Логічні вправи та завдання підвищеного рівня складності для учнів,
   які мають достатній та високий рівні знань.

1) Доведіть, що рівняння 7х² + bх – 23 = 0 при будь-яких значеннях b має один додатний і один від'ємний корені. 2. Знайдіть пропущене число:

VII. Підсумки уроку

В якому з випадків правильно виконано дію?

1) Сума коренів рівняння 5х² – 9х – 2 = 0 дорівнює:

а) -9; б) 1,8; г) -1,8; д) ;

2) добуток коренів рівняння 5х² + 3x – 2 = 0 дорівнює:
а) -2; б) 2; в) 0,4; г) інша відповідь.

VIII. Домашнє завдання

1. Вивчити зміст та схеми доведення теореми Вієта та оберненої тео­реми.
2. Розв'язати вправи на застосування вивчених теорем.
3. На повторення: розв'язати квадратні рівняння за формулою.