Розробка уроку на тему "Теорема Вієта"

Тема. Теорема Вієта

Мета: закріпити знання учнів щодо змісту теореми Вієта для зведе­ного квадратного рівняння та використати їх для формулювання і до­ведення теореми Вієта для квадратного рівняння загального виду; вдосконалити вміння відтворювати вивчені твердження, використову­вати їх для розв'язування завдань, передбачених програмою з мате­матики.

Тип уроку: застосування та вдосконалення вмінь.

Наочність та обладнання: опорний конспект «Теорема Вієта».

Хід уроку

I. Організаційний етап

II. Перевірка домашнього завдання

Математичний диктант

Закінчіть речення:

1. сума х₁ + х₂ коренів рівняння х² – bх + т = 0 дорівнює...;
2. добуток у₁ · у₂ коренів рівняння у² + ау + b = 0 дорівнює...;
3. сума і добуток коренів рівняння х² – 5х + 6 = 0 відповідно дорівнюють...;
4. квадратне рівняння з цілими коефіцієнтами, сума коренів якого — 0,5, а добуток коренів якого дорівнює 2, має вигляд...

III. Формулювання мети і завдань уроку

Після проведеної роботи з перевірки засвоєння матеріалу поперед­нього уроку (перевірка якості виконання математичного диктанту), що передбачає неодноразове відтворення теореми Вієта для квадратного рівняння загального вигляду, формулюємо проблему: чи існує відпо­відним чином записаний зв'язок між коренями і коефіцієнтами квад­ратного рівняння загального вигляду, а також чи можливе застосу­вання виявлених закономірностей у ситуаціях, подібних до тих, що були розглянуті на попередньому уроці.

IV. Актуалізація опорних знань .та вмінь

 З метою успішного сприйняття учнями навчального матеріалу уроку слід активізувати такі знання і вміння учнів: означення квадратного рівняння; види квадратних рівнянь; розв'язування квадратних рівнянь різних видів вивченими способами; форму­лювання теореми Вієта та оберненої до неї теореми для зведе­ного квадратного рівняння; виконання арифметичних дій з дійсними числами.

Виконання усних вправ

1. Перевірте, чи є числа х₁ і х₂ коренями квадратного рівняння:

а) х² – 9х + 14 = 0; х₁ = 2; х₂ = 7;

б) х² + 2х – 3 = 0; х₁ = -1; х₂ = 3;

в) х² + 3,5х – 2 = 0; х₁ = 0,5; х₂ = - 4;

г) 3х² – 7х + 2 = 0; х₁ = ; х₂ = 2.

2. Розв'яжіть рівняння:

а) 2х² – 7 = 1; б) х(х + 2,5) = 0; в) х² – 3х = 0; г) х² + 10х + 25 = 0;

д) 2х² + 4 = 0; є) х² – 6 = 0; ж) х² – х – 2 = 0; з) х² – х + 5 = 0.

V. Застосування знань

План вивчення нового матеріалу

1. Теорема Вієта для квадратного рівняння загального виду.
2. Теорема, обернена до теореми Вієта, для квадратного рівняння за­гального виду.
3. Приклади завдань на застосування вивчених теорем.

 Теорема Вієта для квадратного рівняння загального вигляду та обернена до неї теорема доводяться досить легко через теорему Вієта для зведеного квадратного рівняння.

Тому за умови високої інтелектуальної активності учнів можна за­пропонувати їм вивчення цієї частини нового матеріалу самостійно (або за підручником, або сформулювати твердження разом з учнями, а потім запропонувати їм виконати доведення самостійно).

Щодо прикладів застосування вивчених теорем (зазвичай у цьому розділі розглядаються тільки завдання на знаходження невідомого ко­реня та одного з коефіцієнтів за відомим другим коренем та двома відомими коефіцієнтами квадратного рівняння загального вигляду), то тут автор пропонує ознайомити учнів із деякими прийомами розв'язу­вання квадратних рівнянь, що ґрунтуються на застосуванні теореми, оберненої до теореми Вієта (наприклад, для рівнянь виду

ах² + bx + c = 0, де а + с = b, х₁ = -1, х₂ = ).

VI. Відпрацювання вмінь

Виконання усних вправ

1. Знайдіть суму і добуток коренів рівняння:

а) 2х² – 5х – 2 = 0; б) 3х² – 2х – 1 = 0; в) 5х² + 4х – 1 = 0; г) 7х² – 8х + 1 = 0.

2. Серед рівнянь ах² + bx + c = 0 виберіть такі, в яких:

а) а + с = b; б) а + с = -b.

х² – 2х + 1 = 0; 3х² – 2х – 1 = 0; 5х² + 4х – 1 = 0; 122х² + 33x – 89 = 0.

3. Знайдіть корені рівняння:

а) 3х² – 2х – 1 = 0; б) 3х² + 2х – 1 = 0;

в) 199х² – 100х – 99 = 0; г) 199х² + 100х – 99 = 0.

Виконання письмових вправ

Для реалізації дидактичної мети на цьому уроці слід розв'язати за­вдання такого змісту:

1. Знаходження коренів квадратного рівняння за теоремою, оберне­ною до теореми Вієта.

1) Знайдіть корені рівняння за теоремою, оберненою до теореми Вієта:

а) х² – 3x + 2 = 0; б) х² – 5x + 6 = 0; в) х² + 7x + 12 = 0;

г) х² + 3x + 2 = 0;  д) x² – 5х + 4 = 0; є) х² – 8x – 9 = 0;

ж) х² + 4х + 3 = 0; з) х² – 2х – 3 = 0;  и) х² + 2х – 15 = 0.

2) Знайдіть підбором корені рівняння:

а) х² – 9х + 20 = 0; б) х² + 11x – 12 = 0; в) х² + х – 56 = 0; г) х² – 19x + 88 = 0.

3) Розв'яжіть рівняння:

а) 4х² + 7x + 3 = 0; б) х² + х – 56 = 0; в) х² – х – 56 = 0;

г) 5х² – 18x + 16 = 0; д) 8х² + х – 75 = 0; є) 3х² – 11х – 14 = 0;

ж) 3х² + 11х – 34 = 0; з) х² – х – 1 = 0.

2. Знаходження коефіцієнтів зведеного квадратного рівняння та квад­ратного рівняння загального виду за його відомими коренями.

1) Числа х₁ і х₂ – корені зведеного квадратного рівняння. Запи­шіть це рівняння, якщо:

а) х₁ + х₂ = 4, х₁ · х₂ = 3; б) х₁ + х₂ = -7, х₁ · х₂ = 10.

2) Запишіть зведене квадратне рівняння, яке має корені:

а) 1 і 3; б) -4 і 1,5; в) -4 і -5; г) 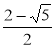і .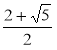

3) При якому значенні а один із коренів рівняння ах² – 3х – 5 = 0 дорівнює 1?

3. Знаходження невідомого кореня та невідомого коефіцієнта квад­ратного (зведеного та загального виду) рівняння, якщо відомий другий корінь та два інші коефіцієнти.

1) Число – 9 є коренем рівняння х² + 10x + q = 0. Знайдіть інший корінь рівняння і коефіцієнт q.

2) Якими можуть бути цілі корені рівняння х² + px + q = 0, якщо:

a) q = 7; б) q = -5; в) q = 9; г) q = -8?

3) Один із коренів рівняння х² – 13х + q = 0 дорівнює 12,5. Знайдіть  другий корінь і коефіцієнт q.

4. Логічні вправи та завдання підвищеного рівня складності для учнів, які мають достатній та високий рівні знань.

1) Рівняння х² + рх + 8 =0 має додатні корені, один із яких у 4 рази більше від іншого. Знайдіть корені рівняння та коефіцієнт р.

2) Доведіть, що рівняння 12х² + 70х + a² + 1 = 0 при будь-яких зна­ченнях а не має додатних коренів.

3) Знайдіть пропущений вираз:

5. На повторення: розв'язати квадратні рівняння, визначивши попе­редньо їх вид.

 Вправи, винесені на урок, мають на меті сприяти закріпленню змісту теореми Вієта та оберненої до неї теореми, відпрацюван­ня навичок використання вивченої теорії в стандартних ситуаціях.

VII. Підсумки уроку

В якому випадку правильно записані співвідношення для коренів?

а) х² + 3х + 2 = 0, х₁ + х₂ = 3, х₁ · х₂ = 2;

б) 3х² – 2х – 1 = 0, х₁ + х₂ = , х₁ · х₂ = , х₁ = 1;

в) 3х² + 2х – 5 = 0, х₁ + х₂ = , х₁ · х₂ = , х₁ = - 1.

VIII. Домашнє завдання

1. Вивчити зміст теореми Вієта та оберненої до неї теореми для квад­ратного рівняння загального вигляду.
2. Розв'язати завдання на застосування вивченої теорії (знайти корені квадратного рівняння за теоремою, оберненою до теореми Вієта; знайти невідомий корінь та невідомий коефіцієнт квадратного (зведеного та загального виду) рівняння, якщо відомий другий корінь та два інші коефіцієнти).
3. На повторення: завдання, що передбачають розв'язування квадрат­них рівнянь (повних та неповних із застосуванням вивчених у темі 5 способами).