Формули доповнення. Значення тригонометричних фун¬кцій кутів 30°, 45°, 60°. Розв'язування задач

Тема.  Формули доповнення. Значення тригонометричних фун­кцій кутів 30°, 45°, 60°. Розв'язування задач

Мета: закріпити знання учнями змісту формул доповнення та чис­лових значень тригонометричних функцій кутів 30°, 45°, 60°. Сформу­вати вміння застосовувати формули до розв'язування задач.

Тип уроку: застосування знань, умінь та навичок.

Наочність та обладнання: конспект 22.

Хід уроку

I. Організаційний етап

II. Перевірка домашнього завдання

Учні виконують роботу з перевірки домашнього завдання у формі «Знайди помилку» (запис готового розв'язання домашніх задач із «помилками» виконано на дошці заздалегідь).

Засвоєння змісту теоретичного матеріалу уроку перевіряється під час самостійного виконання учнями вправ на вписування.

Заповніть пропуски записами так, щоб рівності стали правильними (α, β, χ – гострі кути).

а) sin (90° – α) = ...;

б) cos ( ... – β) = sin β;

в) tg (90° – ...) = ctg χ;

г) ... (90° – ...) = tg β;

д) sin ... + cos 45° = + ... = ...;

є) 3 tg ... + 5 ctg ... = 3 + 5;

ж) 2 … 60° + 3 tg ... = 1 – 3 = ...;

з) sin ... – tg... = – = ...

III. Формулювання мети і завдань уроку

Загальна мета уроку — закріплення знань учнів з теми та опанування способів застосування цих знань, формування вмінь оперувати набутими знаннями в стандартних та нестандартних ситуаціях.

IV. Актуалізація опорних знань

Виконання усних вправ

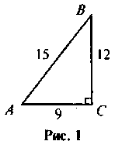
1. Знайдіть: cos В, tg A (рис. 1).
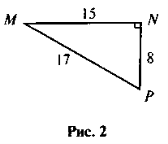
2. Знайдіть: sin Р, cos M (рис. 2).
3. Спростіть вираз:

а) ;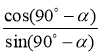 

б) sin² α + sin² (90° – α);  в) 1 – cos² (90° – α).

4. Обчисліть:

a) 2 sin 30° + 3 cos 60°;  б) 6 sin 30° – tg 45°;

в) cos 60° · sin 30°;  г) 4 cos 30° – tg 60°;

д) 2 cos 60° – 3 tg 45°; є) 1 – 2 cos² 45°;

ж) cos² 30° – 2 sin² 30°; з) sin² 45° + sin 30°;  и) .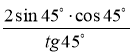

5. Чому дорівнює тангенс гострого кута, якщо синус і косинус цього кута рівні між собою?
6. У прямокутному трикутника ABC катет а більший від катета b. Що більше: cos А чи cos В?

V. Застосування знань та вмінь

Застосування знань у стандартних ситуаціях

1. Кути А і В — гострі кути прямокутного трикутника. Знайдіть:

a) tg А, якщо sin В = ; б) sin В , якщо ctg A = ;

в) sin² А + sin² В .

2. Обчисліть без допомоги таблиць:

a) cos² 30° – 2 sin² 30°; б) 3 cos² 45° – 2 cos²60°; в) 4 sin 30° – cos 30°.

3. Обчисліть без допомоги таблиць:

а) (cos 30° + cos 45°)(cos 45° – sin 60°);

б) (sin 60° – sin 30°)(cos 60^o + cos 30°);

в) (1 + sin 30° + sin 60°)(3 cos 60° – sin 60°).

4. Спростіть вираз:

а) (1 + ctg(90° – α))² + (1 – ctg(90° – α))²; 

б) ;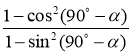

в) (sin(90° – α) tg α) + .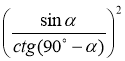

Застосування знань у нестандартних ситуаціях

1 (опорна). За зростання гострого кута синус і тангенс зростають, а косинус і котангенс спадають. Доведіть.

2. Обчисліть значення виразу tg 15° tg 30° tg 45° tg 60° tg 75°.

3. Подайте вираз у вигляді суми добутків синусів деяких кутів на числа:

а) + – ;      б) – 0,25 + 2 – 3.

4. Запишіть вираз у вигляді суми добутків косинусів деяких кутів на
числа:

а) – + 4;    б) 1 – + 2 – .

5. Запишіть вираз у вигляді суми добутків тригонометричних функ­цій кута 30° на деякі числа:

а) 5 – 4+; б) + 4 – 2.

6. Розташуйте в порядку зростання:

а) sin 12°, sin 65°, sin 38°, sin 25°;

б) cos 52°, cos 10°, cos 80°, cos 20°;

в) tg 37°, tg 87°, tg 77°, tg 27°, tg 57° .

7. Чи правильно, що:

a) sin² 28° + sin² 62° = 1;       б) tg 20° – tg 70° = 1 ; в) sin³ α + cos³ α < 1?

8. Що можна сказати про гострий кут A (A = α), якщо відомо, що:
а) sin α > sin 47°; б) cos α > cos 31°;  в) tg α > tg 20°; г) sin α < 0,5;

д) tg α > 1 ; e) cos α >  ; ж) sin α > cos α.

 Під стандартними в цьому випадку розуміють задачі, в умові яких є вказівки на ті твердження, які слід застосовувати під час розв'язування.

Нестандартні ситуації як завжди представлені задачами, в яких слід застосовувати додатковий матеріал або взагалі доводити нові опорні факти, а також виявляти елементи творчого мислення.

VI. Підсумки уроку

Підбиваючи підсумки уроку, необхідно описати види задач на застосування матеріалу §20 та дати словесний опис схеми їх розв'язання.

VIII. Домашнє завдання

Повторити зміст та доведення теореми про формули доповнення та значення тригонометричних функцій кутів 30°, 45°, 60°; означення й властивості тригонометричних функцій гострого кута та тригонометричні, тотожності.

Розв'язати задачі.

1. Знайдіть гострий кут х, якщо: a) ctg x = tg 14°; б) tg x = ctg x.
2. Знайдіть:

а) sin α, cos α і tgα, якщо tg(90° – α) = ;

б) cos² α + cos² (90° – α).

3. Порівняйте:

a) sin 23° і cos 65°; б) tg 36° і ctg 64°.

4. Доведіть, що tg 1° · tg 2° ·... · tg 88° · tg 89° = 1.