Розв'язування прямокутних трикутників
Тема. Розв'язування прямокутних трикутників
Мета: працювати над засвоєнням учнями змісту поняття «розв'язати трикутник» та схем розв'язання чотирьох основних задач на знаходження невідомих сторін прямокутного трикутника. Сформувати вміння відтворювати зміст вивчених схем, а також застосовувати їх для розв'язування прямокутних трикутників.
Тип уроку: застосування знань, умінь та навичок.
Наочність та обладнання: конспект 2.3.
Хід уроку
I. Організаційний етап
II. Перевірка домашнього завдання
За готовими рисунками проводиться усне обговорення плану розв'язання задачі, оголошується правильна відповідь.
Засвоєння теоретичного матеріалу (правил обчислення сторін прямокутного трикутника) перевіряється під час виконання математичного диктанту.
Математичний диктант
- Закінчіть речення: Катет, що лежить проти гострого кута, дорівнює добутку гіпотенузи на ...
- Закінчіть речення: Катет, що лежить проти гострого кута, дорівнює добутку іншого катета на ...
- Закінчіть речення: Катет, прилеглий до даного гострого кута, дорівнює добутку гіпотенузи на ...
- Закінчіть речення: Гіпотенуза дорівнює відношенню ...
-
У трикутнику ABC
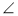 C = 90° AC = а см,
C = 90° AC = а см, 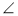 B = β. Як знайти АВ
B = β. Як знайти АВ 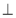 ВС ?
ВС ?
-
У трикутнику MNK
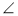 N = 90°, MN = а см,
N = 90°, MN = а см,  M = α. Як знайти МК ? NК ?
M = α. Як знайти МК ? NК ?
III. Формулювання мети і завдань уроку
З метою формування розуміння учнями логіки вивчення матеріалу уроку, та кращого його засвоєння, а також щоб мати можливість провести певні аналогії, вчитель ставить учням такі запитання:
- Для яких фігур вивчались співвідношення на уроках геометрії останнім часом?
- Які властивості прямокутного трикутника ви знаєте?
- За якими ознаками можна встановити, шо-два прямокутні трикутники рівні?
-
За якими елементами можна побудувати прямокутний трикутник?
Скількома способами це можна зробити в певному положенні відносно даної півпрямої ? - Порівняйте відповіді на запитання 3 і 4. За якими елементами, виходячи з цього порівняння, визначається певний прямокутний трикутник? Чи можна знайти за цими даними всі інші невідомі елементи цього трикутника?
Відповідаючи на запитання, учні поступово усвідомлюють, що, виходячи з ознак рівності прямокутних трикутників, певний прямокутний трикутник однозначно задається такими парами елементів: гіпотенузою та гострим кутом; катетом і гострим кутом; гіпотенузою і катетом; двома катетами.
Отже, завдання на урок — з'ясувати способи обчислення невідомих елементів прямокутного трикутника за кожним із чотирьох виділених пар елементів, а також закріплення вмінь використовувати ці способи для розв'язування практичних задач.
IV. Актуалізація опорних знань
Виконання усних вправ
-
Обчисліть: a) cos α · tg α; б) sin α · tg α (0° < α < 90°), якщо cos α =
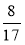 .
.
-
 Заповніть пропуски: a = c · ...
Заповніть пропуски: a = c · ...  B, b = a · ...
B, b = a · ... 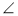 A,
A, 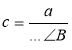 ,
,  .
.
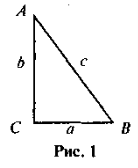
- АВ = 10 см, cos А = 0,6 (рис. 1), Знайдіть BC, AC, sin В, tg A.
- AC = 20 см, tg В = 2 (рис. 1). Знайдіть ВС, sin А.
-
На рисунку 2
 ACB = 90°, BD
ACB = 90°, BD 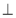 AD .
AD .
 а)
а) ![]() CАВ = α, АC = b,
CАВ = α, АC = b, ![]() DAB = β. Знайдіть ВС.
DAB = β. Знайдіть ВС.
б) BC = c, ![]() ABC = α,
ABC = α, ![]() ABD = β. Знайдіть PAKD.
ABD = β. Знайдіть PAKD.
V. Засвоєння знань
План вивчення нового матеріалу
- Що означає термін «розв'язати трикутник (прямокутний)»?
- Приклади задач на розв'язування прямокутних трикутників.
На відміну від традиційного підручника геометрії, у новому підручнику вже у 8 класі пояснюється зміст поняття «розв'язати трикутник (прямокутний)», а також містяться приклади розв'язування чотирьох видів задач на знаходження невідомих елементів прямокутного трикутника. Це дозволяє сформувати в учнів алгоритмічний підхід до розв'язування трикутників і спростити процес розв'язування багатьох геометричних задач.
Вивчення матеріалу проводиться таким чином: спочатку розбирається зміст поняття «розв'язати трикутник (прямокутний)», далі вивчаються розв'язання кожної задачі з тим, щоб далі узагальнити види задач та схеми розв'язання задач окремого виду. Результати цієї роботи фіксуються в зошитах учнів, від яких вимагається не стільки бездумне відтворення формул, скільки розуміння геометричних співвідношень, що за цими формулами стоять (записи схем розв'язання задач — див. конспект 23).
IV. Формування первинних умінь
Виконання усних вправ
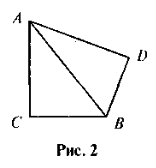
- Дано: АВ = ВС, BD — медіана (рис. 3). Знайдіть BD, AC.
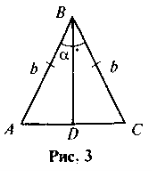
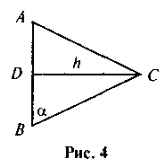
- Дано: AC = ВС, CD — медіана (рис. 4). Знайдіть АВ.
Виконання письмових вправ
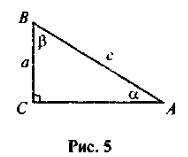
- Розв'яжіть прямокутний трикутник (рис. 5) за гіпотенузою і гострим кутом с = 8, α = 30°.
- Розв'яжіть прямокутний трикутник (рис. 5) за катетом і гострим кутом а = 2, β = 45°.
-
Розв'яжіть прямокутний трикутник (рис. 5) за гіпотенузою і катетом: с = 9
 , а = 9.
, а = 9.
-
Розв'яжіть прямокутний трикутник (рис. 5) за двома катетами: а = 6
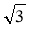 , b = 6.
, b = 6.
- Відрізок BD — висота прямокутного трикутника ABC, проведена до гіпотенузи. Розв'яжіть трикутник ABC, якщо:
a) BD = 4![]() ,
, ![]() DBC = 60°; 5) AD = 9,
DBC = 60°; 5) AD = 9, ![]() C = 10°.
C = 10°.
- У рівнобічну трапецію вписано коло, радіус якого дорівнює 12 см. Знайдіть основи трапеції, якщо довжина бічної сторони дорівнює 25 см.
- У колі з центром О і радіусом 10 см проведено хорду АВ довжиною 16 см. Із центра кола до хорди проведено перпендикуляр, який перетинає хорду в точці Е, а коло — у точці F. Знайдіть довжину відрізка EF.
- Радіуси двох кіл дорівнюють 8 см і 3 см, а відстань між їх центрами — 13 см. Знайдіть довжину їх зовнішньої спільної дотичної.
Вправи на закріплення алгоритмів, вивчених на уроці, підібрані таким чином, щоб обчислення невідомих елементів трикутників можна було виконати, використовуючи значення тригонометричних функцій кутів 30°, 45°, 60°.
Підготовкою до наступного уроку є додаткові вправи. Розв'язавши їх, учні повторюють властивості чотирикутників, які наступного уроку треба буде використовувати разом із алгоритмами розв'язання прямокутник трикутників.
VII. Підсумки уроку
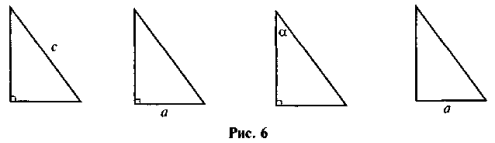
Які елементи слід знати додатково, щоб мати можливість розв'язати трикутники, що зображені на рисунку 6.
VIII. Домашнє завдання
Вивчити зміст матеріалу «Приклади розв'язання прямокутних трикутників».
Розв'язати задачі.
- Розв'яжіть прямокутний трикутник (рис. 5), якщо:
а) с = 12, α = 28°; б) а = 8, β = 40°.
- Розв'яжіть прямокутний трикутник (рис. 5), якщо:
а) а = 6, с = 10; б) а = 5, b = ![]() .
.
- Відрізок BD — висота прямокутного трикутника ABC, проведена до гіпотенузи. Розв'яжіть трикутник ABC, якщо BD = 3, DC = 4.
Повторити властивості рівнобічної трапеції, прямокутної трапеції, метричні співвідношення в прямокутному трикутнику.


про публікацію авторської розробки
Додати розробку
