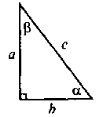
Співвідношення між сторонами і кутами прямокутного трикутника

Тема. Співвідношення між сторонами і кутами прямокутного трикутника

Мета: домогтися засвоєння учнями змісту правил знаходження не­відомих сторін прямокутного трикутника, що випливають з означень тригонометричних функцій гострого кута; формувати вміння відтворю­вати зміст цих правил, а також застосовувати правила для знаходжен­ня невідомих сторін прямокутного трикутника. Закріплювати знання числових значень тригонометричних функцій кутів 30°, 45°, 60°, а та­кож означення та властивостей тригонометричних функцій, вивчених на попередніх уроках.

Тип уроку: засвоєння вмінь та навичок.

Наочність та обладнання: конспект 23.

Хід уроку

I. Організаційний етап

II. Перевірка домашнього завдання

Самостійна робота

Варіант 1

1. Обчисліть: .
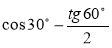2. Спростіть вираз .

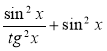Варіант 2

1. Обчисліть: .
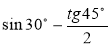2. Спростіть вираз cos² х tg² х + cos² х.

Варіант 2

1. Обчисліть: 2 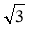· (sin 60° – tg 30°).
2. Спростіть вираз .

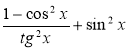Варіант 4

1. Обчисліть: 2 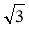· (tg 30° – cos 30°).
2. Спростіть вираз .

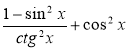III. Формулювання мети і завдань уроку

Перш ніж сформулювати мету уроку, вчитель наводить відомі учням приклади співвідношень між величинами, записаних у вигляді формул, та нагадує про можливість математичного перетворення формул (тобто вираження з формул одних величин через інші). Найбільш тривіальний приклад — закон рівномірного прямолінійного руху: s = vt, з якого можна виразити кожну з величин, за допомогою яких цей закон записано. Проводячи аналогію з матеріалом, що вивчається на уроках геометрії, нескладно дійти висновку, що і для геометричних співвідношень можливо виразити одну величину через інші.

Отже, мета уроку — вивчення таких співвідношень між елементами прямокутного трикутника, які є наслідками перетворень відомих співвідношень у прямокутному трикутнику.

IV. Актуалізація опорних знань

Виконання усних вправ

1. Дайте означення синуса, косинуса і тангенса гострого кута прямо­кутного трикутника.
2. Доведіть основну тригонометричну тотожність.
3. Доведіть формули доповнення.
4. Назвіть значення тригонометричних функцій кутів 30°, 45°, 60°.
5. Опишіть розв'язування прямокутного трикутника:

а) за гіпотенузою і гострим кутом;

б) за катетом і гострим кутом;

в) за гіпотенузою і катетом;

г) за двома катетами.

6. Із рівності 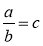виразіть а, b. Прочитайте вихідну та здобуті рів­ності, використовуючи поняття «добуток», «відношення».
7. a, b — катети, с — гіпотенуза прямокутного трикутника. Порівняй­те записи: a = c sin α, b = c cos α. Що в них спільного? Що відмінно­го? На який із цих записів більше схожий запис b = c sin α ? Чому?

V. Засвоєння знань

План вивчення нового матеріалу

1. Правило знаходження катета, протилежного гострому куту прямо­кутного трикутника.
2. Правило знаходження катета, прилеглого до гострого кута прямо­кутного трикутника.
3. Правило знаходження гіпотенузи.
4. Приклади застосування.

 Зміст матеріалу п. 21.1 нового підручника суттєво відрізняється від відповідного матеріалу попереднього підручника тим, що в ньо­му подано обґрунтування різних способів знаходження невідомих сторін прямокутного трикутника, а також описано загальну схему дій для знаходження сторони прямокутного трикутника із вико­ристанням означення тригонометричних функцій.

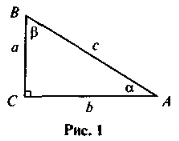Роботу з вивчення  нового матеріалу можна провести або за підручником, або запропонувавши учням виконати таке завдання:

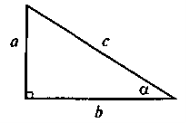
1. Для трикутника рис. 1 запишіть у вигляді формул означення всіх тригонометричних функцій.
2. Із кожної записаної рівності виразіть усі можливі сторони прямокутного три­кутника.
3. Прочитайте здобуті рівності, викорис­товуючи поняття «добуток», «відношен­ня», та назви сторін прямокутного три­кутника.
4. Порівняйте здобуті рівності, розбийте їх на групи за схожими елементами.
5. Узагальніть результати (для кожної з утворених груп скласти загаль­не правильно).
6. Порівняйте виведені правила з поданими в підручнику. Складіть конспект.

VI. Формування первинних умінь

Виконання усних вправ

1. Як знайти гіпотенузу прямокутного трикутника, коли відомі катет і гострий кут?
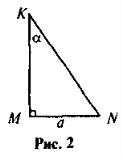2. Як знайти гострий кут прямокутного трикут­ника, коли відомі протилежний цьому куту катет і гіпотенуза?
3. Як знайти гострий кут прямокутного трикут­ника, коли відомі прилеглий до цього кута ка­тет і гіпотенуза?
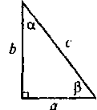
4. У прямокутному трикутнику KMN (рис. 2) відомі катет MN і кут К. Виразіть через них другий катет і гіпотенузу трикутника.

Виконання письмових вправ

1. У прямокутному трикутнику катет завдовжки 7 см є прилеглим до кута 60°. Знайдіть гіпотенузу трикутника.
2. У прямокутному трикутнику гіпотенуза дорівнює 20 см, а синус од­ного з кутів — 0,6. Знайдіть катети трикутника.
3. Визначте невідомі сторони прямокутного трикутника ABC (C = 90°), якщо:

1) АВ = с, A = α; 2) AC = b, B = β; 3) ВС = а, B = β.

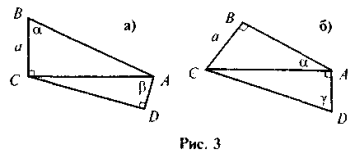
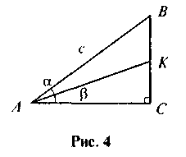
4. За рис. 3 визначте довжини відрізків AD і CD.

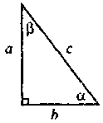
5. У прямокутному трикутнику ABC (рис. 4) АВ = с, 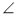BAC = α, KAC = β. Знайдіть довжину відрізка ВК.
6. Знайдіть бічну сторону рівнобедреного трикутника, якщо його ос­нова дорівнює 24 см, а медіана, проведена до бічної сторони, дорів­нює 30 см.
7. У рівнобічній трапеції діагональ дорівнює 17 см, а висота трапеції — 8 см. Знайдіть середню лінію трапеції.
8. Основа AD рівнобічної трапеції ABCD ділиться висотою BE на відрізки довжиною 5 см і 16 см, а довжина бічної сторони трапеції дорівнює 13 см. Знайдіть діагоналі трапеції.
9. Сторони трикутника дорівнюють 13 см, 14 см і 15 см. Знайдіть ви­соту трикутника, проведену до його середньої сторони.

 Залежно від рівня інтелектуальної активності учнів, розв'язування запропонованих задач ведеться з використанням або правил зна­ходження невідомих сторін прямокутних трикутників (конспект 23), або з використанням схеми дій, описаної в підручнику. Проте за будь-якого способу розв'язання, пошук невідомої сторони три­кутника слід починати з аналізу умови (що відоме, що — невідо­ме) і тільки після цього відтворювати відповідне твердження, щоб використати його для виконання обчислень.

VII. Підсумки уроку

Користуючись рисунком 5, визначте, які з даних тверджень правильні:

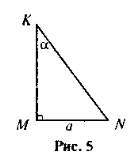а) ; б) MK = KN sin α;

в) KN = MN tg α; г) .

VIII. Домашнє завдання

Вивчити зміст співвідношень між сторонами й кутами прямокутного трикутника.

Розв'язати задачу.

У прямокутному трикутнику гіпотенуза дорівнює 8 см, а один із катетів — 4 см. Знайдіть гострі кути трикутника.

Повторити властивості паралелограмів та трапецій.