Формули подвійного аргументу

Тема. Формули подвійного аргументу. Розв’язання вправ.

Мета: домогтися засвоєння тригонометричних формул подвійного аргументу; закріпити знання цих формул під час розв’язання вправ; розвивати вміння порівнювати, самостійно мислити; виховувати інтерес до математики, удосконалювати навички самоконтролю.

Тип урок: засвоєння нових знань, формування вмінь.

Обладнання: конспект, підручник Мерзляк А.Г. Алгебра і початки аналізу 10 клас профільний рівень.

Література:

• Для вчителя:

А.Г. Мерзляк Алгебра і початки аналізу 10 клас профільний рівень;

М.И. Сканави Сборник задач по математике для поступающих в вузы.

• Для учнів:

А.Г. Мерзляк Алгебра і початки аналізу 10 клас профільний рівень;

Хід уроку

I. Організаційний етап.

Проконтролювати щоб учні підготували класну дошку. Перевірка готовності учнів до уроку.

II. Перевірка домашнього завдання.

III. Формулювання мети і завдань уроку.

На попередньому уроці ми вивчили тригонометричні формули додавання. Ці формули мають багато наслідків. Тригонометричні формули подвійного аргументу є наслідком формул додавання. Тобто тригонометричні формули додавання дозволяють виразити , , через тригонометричні функції кута . Тож наша мета – це вивчення формул подвійного аргументу.

IV. Актуалізація опорних знань.

Повторення формул додавання.

Обчисліть:

1) ;

2) ;

3) ;

4) ;

5) ;

6) .

V. Засвоєння знань.

План

1. Вивчення формул синуса подвійного аргументу.

2. Вивчення формул косинуса подвійного аргументу.

3. Вивчення формул тангенса подвійного аргументу.

Формули, які виражають тригонометричні функції аргументу через тригонометричні функції аргументу , називаються формулами подвійного аргументу.

1) Запишемо формулу для синуса суми: ; Покладемо , отримаємо: ;

2) Аналогічно для наступних функцій:

; ;

Виразимо із тригонометричної одиниці і підставимо у нашу формулу: ;

Тепер виразимо і підставимо у формулу: .

3) Для тангенса: ; ;

Формули для синуса і косинуса виконуються для будь-яких значень аргументу, а формула тангенса подвійного аргументу виконується тільки для тих значень аргументу , для яких визначені і , тобто , і , .

VI. Закріплення нового матеріалу.

1) Виразіть через функції вдвічі меншого аргументу:

А) ;

Б) ;

В) ;

2) Спростіть вираз:

1. ;
2. ;
3. ;
4. ;
5. ;
6. ;
7. ;
8. ;
9. ;
10. ;
11. ;
12. ;
13. 
14. ;
15. ;
16. ;

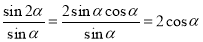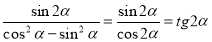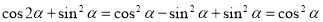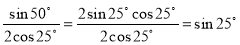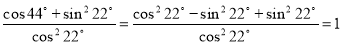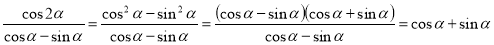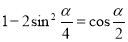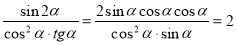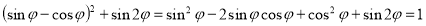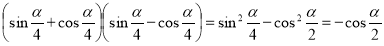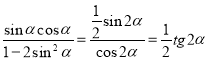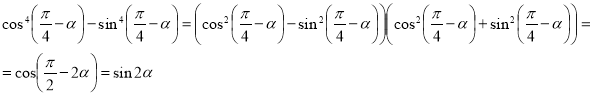
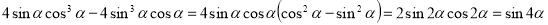3) Обчисліть:

1. ;
2. ;
3. ;
4. ;
5. ;
6. .

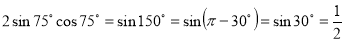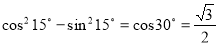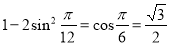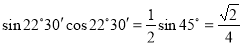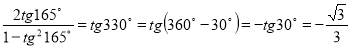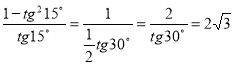4) Знайдіть , якщо і .

; ; ; ;

.

5) Знайдіть , якщо: а) ; б) і .

а) ; ;

б) ; ; ; ; ;

6) Спростіть вирази:

1. 
2. .

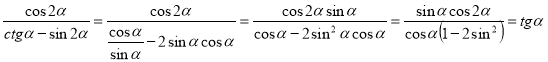7) Довести, що .

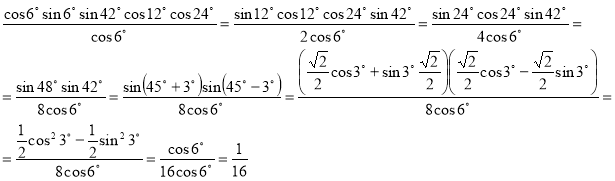
VII. Підбиття підсумків уроку.

Запитання до класу:

1. Яку групу формул ми сьогодні вивчили?
2. Чому дорівнюють , , ?
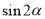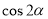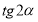3. Яким чином ми отримали дані формули?

VIII. Домашнє завдання.

§42, вивчити формули, №887, 888, 918(3-6), 920(1-2).