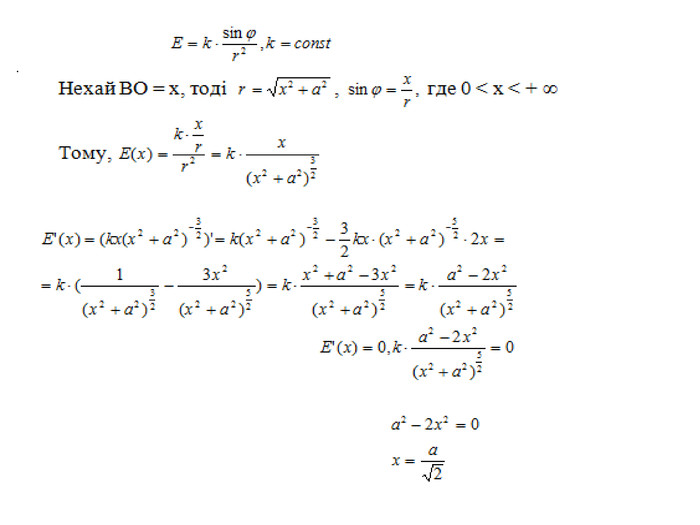Формування соціальних компетентностей учнів через розв’язання прикладних задач на знаходження найбільших та найменших значень величин
Про матеріал
Показати ефективність використання на уроках математики методу математичного моделювання для формування соціальних компетентностей учнів через розв’язання прикладних задач на знаходження найбільших та найменших значень величин
Перегляд файлу
Зміст слайдів
ppt
До підручника
Алгебра (академічний, профільний рівень) 11 клас (Нелін Є.П., Долгова О.Є.)
До уроку
5.3. Найбільше і найменше значення функції Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку