Квадратична функція в задачах з параметрами

 

Квадратична функція в задачах з параметрами.

Квадратична функція є основною в шкільному курсі математики. Тому, природно, вона формує великий клас задач з параметрами, різноманітних за формою і змістом, але об’єднаних однією ідеєю – в основі їх розв’язання лежать властивості функції .

§1. «Каркас» квадратичної функції.

Фактично всі важливі властивості квадратичної функції задаються таблицею, що представлена на малюнку 26.

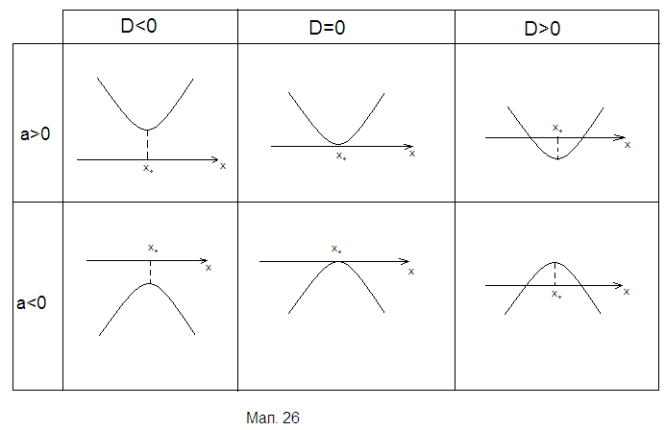
Наведена схема демонструє, що дискримінант , старший коефіцієнт відповідного функції квадратного тричлена, абсциса вершини параболи конструюють «каркас», на якому будується теорія квадратичної функції.

 

А. Дискримінант, старший коефіцієнт.

3.1. Знайти всі значення параметра , при яких система рівнянь 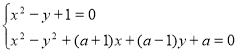має розв’язки.

Розв’язання:

Друге рівняння запишемо у вигляді: або . Якщо , то перше рівняння набуває вигляду і дійсних коренів немає.

Отже, , тоді . Необхідно і достатньо, щоб .

Відповідь: .

3.2. Знайти всі значення , для яких нерівність виконується для всіх значень .

Розв’язання:

Якщо , то умова задачі не виконується.

При маємо - розв’язків немає.

При необхідно і достатньо, щоб , тобто .

Відповідь: .

3.3. При яких значеннях нерівність 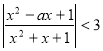виконується для всіх ?

Розв’язання:

Перепишемо дану нерівність у вигляді: . Оскільки для всіх , то остання нерівність еквівалентна системі: 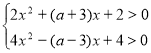. Для того, щоб ця система виконувалась для всіх , дискримінанти відповідних квадратних тричленів повинні бути невід’ємними:

.

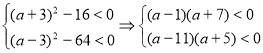Відповідь: .

3.4. Знайти всі цілі значення , при яких нерівність 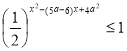виконується при будь-якому .

Розв’язання:

Переходимо до еквівалентної нерівності: . Необхідно, щоб . Загальний розв’язок . З якого легко отримуємо

Відповідь: .

3.5. При яких значеннях параметра для будь-якого виконується нерівність ?

Розв’язання:

Оскільки 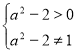, то .

Розглянемо два випадки:

1) . Маємо: . З урахуванням умови остання нерівність не може виконуватись для всіх .

2) . Тоді . Необхідно: або .

Відповідь: або .

3.6. Дано два многочлена: та . При яких значеннях один із многочленів має корінь, а інший ні?

Розв’язання:

Умові задачі відповідає сукупність двох систем нерівностей: 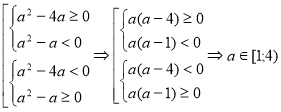. Випадок розглянемо окремо. В цьому випадку - коренів немає; - корінь є.

Відповідь: або .

3.7. Знайти найменше , при якому існує розв’язок рівняння .

Розв’язання:

Запишемо рівняння у вигляді і розглянемо його як квадратне відносно . Для існування розв’язку необхідно вимагати, щоб . Маємо: . Тепер залишається знайти такі , при яких отримана квадратна нерівність має хоча б один розв’язок. Звернення до малюнку 26 дає змогу знайти необхідну умову: . Найменше значення .

Відповідь: .

3.8. При яких значеннях параметра існує єдина пара чисел , що задовольняє співвідношення ?

Розв’язання:

Запишемо рівняння у вигляді: і розглянемо його як квадратне відносно . Для коректності цього кроку спочатку розглянемо значення . Тоді і будь-яка пара є розв’язком, тобто єдиності немає. Якщо , то . При для будь-якого , отже дане рівняння має безліч розв’язків. При дискримінант стає недодатнім, і існування єдиності розв’язку забезпечується лише умовою .

Відповідь: .

3.9. Знайти при яких система має єдиний розв’язок.

Розв’язання:

З першого рівняння маємо: . Друге рівняння набуває вигляду: . Це рівняння має один розв’язок за умов: або . Крім того, якщо квадратне рівняння має два розв’язки, один з яких , то система має єдиний розв’язок. Це можливо за умови .

Відповідь: .

3.10. Знайти , при яких система 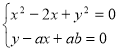має розв’язки для будь-яких .

Розв’язання:

Підставляючи в перше рівняння, отримаємо: , звідки . Знаходимо . Залишається з’ясувати, при яких нерівність виконується при будь-яких . Очевидно, що це відбувається лише за умови .

Відповідь: .

3.11. При яких значеннях рівність є тотожністю.

Розв’язання:

Запишемо рівність у вигляді: . Для того, щоб ця рівність була тотожністю (тобто виконувалась при всіх ) необхідно .

Відповідь: , .

3.12. Знайти при яких система 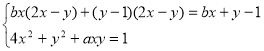має не менше п’яти розв’язків.

Розв’язання:

Перше рівняння системи запишемо у вигляді: . Тому система еквівалентна сукупності двох систем: 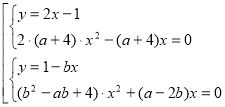. Якщо другі рівняння систем квадратні або лінійні, то система не може мати більше чотирьох розв’язків. Тому необхідно: , тоді будь-яке; або 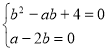, звідки або .

Відповідь: або .

 

 

Б. Вершина параболи.

3.13. При яких значеннях найбільше значення тричлена менше чотирьох?

Розв’язання:

Необхідно, щоб (для цього знову треба звернутись до мал. 26). Координати вершини параболи: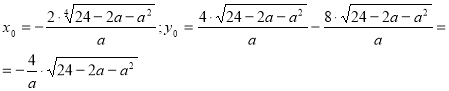

Отримуємо необхідні умови: .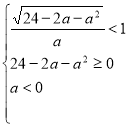

Відповідь: .

3.14. Знайти найменше та найбільше значення функції на відрізку .

Розв’язання:

Дана функція спадає на інтервалі і зростає на інтервалі , де   - координати вершини параболи. Цих міркувань достатньо, щоб записати відповідь. У цьому допоможе мал. 27.

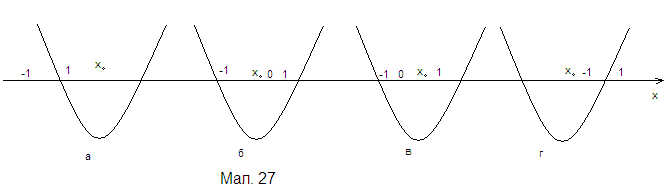
а) Якщо , тобто , то .

б) Якщо , тобто , то .

в) Якщо , тобто , то .

г) якщо , тобто , то .

Відповідь: : ;

                   : ;

                     : ;

                     : .

3.15. Нехай належить множині розв’язків нерівності . Яке при цьому найбільше значення виразу ?

Розв’язання:

Розв’язком нерівності є множина . Абсциса вершини параболи .

Відповідь: якщо , то ;

                   якщо , то ;

                   якщо , то ;

                   якщо , то ;

                   якщо , то ;

                   якщо , то ;

                   якщо , то .

3.16. При яких дійсних найбільше значення функції на відрізку від’ємне?

Розв’язання:

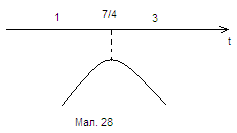Оскільки , то . Тоді шуканими значеннями параметра будуть ті, при яких найбільше значення функції на відрізку від’ємне. Звернемось до графічного образу (мал. 28).

Необхідно , тобто .

Відповідь: .

3.17. Дійсні числа такі, що 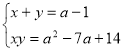. При яких сума приймає найбільше значення?

Розв’язання:

Маємо: . Своє найбільше значення функція приймає при . . Здавалося б, це розв’язок. Але при дана система набуває вигляду і розв’язків немає.

З’ясуємо, при яких система має розв’язки. Підставимо в друге рівняння. Маємо: . Дискримінант цього рівняння . Розв’язком нерівності буде проміжок . Саме при цих дана система має розв’язки. Залишається з’ясувати, при яких функція приймає найбільше значення на відрізку . Абсциса вершини параболи , отже при функція приймає найбільше значення.

Відповідь: .

3.18. Знайти всі значення , при яких вершини двох парабол та  лежать по різні сторони від прямої .

Розв’язання:

Маємо: - вершина параболи ; - вершина параболи . Для параболи ; для параболи . Очевидно, положення парабол, при якому вони лежать по різні сторони від прямої , забезпечується сукупністю: 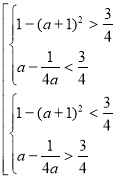. Ця сукупність рівносильна нерівності: .

Відповідь: .

§2. Корені квадратичної функції.

А. Теорема Вієта.

3.19. Нехай - корені рівняння . Обчислити .

Розв’язання:

За теоремою Вієта: .

.

Відповідь: .

3.20. Знайти всі значення параметра , при яких рівняння має два різних кореня і сума цих коренів від’ємна.

Розв’язання:

Спочатку знайдемо всі , для яких рівняння має два різних розв’язки.

1) . Звідки або . З урахуванням умови маємо .

2) 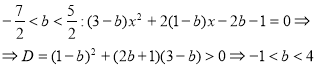, тому - розв’язок.

3) виконується для всіх , оскільки .

Отже, або .

На цій множині повинна виконуватись умова: .

Відповідь: або або .

3.21. При яких різниця коренів рівняння дорівнює їх добутку?

Розв’язання:

. За теоремою Вієта: .

Відповідь: .

3.22. При яких рівняння має два різних дійсних корені, які задовольняють умову ?

Розв’язання:

Дискримінант рівняння: і .

, і скориставшись теоремою Вієта, отримаємо: .

Відповідь: або .

3.23. Знайти від’ємні корені рівняння .

Розв’язання:

Дискримінант цього рівняння . Корені мають вигляд: . Розглянемо вираз . Якщо , то рівняння має один від’ємний корінь. Отже, при   .

Якщо , то , тому обидва корені повинні бути від’ємними, але .

Якщо , то обидва корені від’ємні.

Відповідь: якщо , то ; якщо , то .

3.24. Знайти всі , при яких система 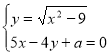має єдиний розв’язок.

Розв’язання:

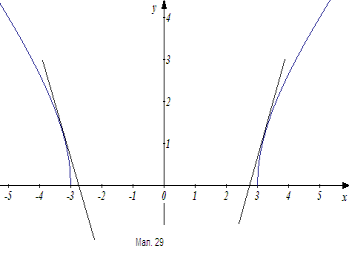Скористаємось геометричною інтерпретацією (мал. 29). З другого рівняння . При або , тому або . Для того, щоб система мала єдиний розв’язок необхідно або . Крім того, може мати один розв’язок, якщо дискримінант рівняння дорівнює нулю. Звідки .

Відповідь: або або .

3.25. При яких значеннях параметра рівняння має єдиний розв’язок?

Розв’язок:

Нехай . Маємо: . Дискримінант цього рівняння при . Тоді . При єдиний розв’язок.

Корені квадратного рівняння: . При маємо лише одне додатне значення .

Відповідь: або .

3.26. Знайти всі значення параметра , для яких нерівність має хоча б один розв’язок.

Розв’язання:

Нехай . Дискримінант рівняння повинен бути невід’ємним. або . Корені рівняння не повинні бути обидва від’ємними.

При вони обидва додатні.

При необхідно виконання умови , отже для цих обидва корені від’ємні.

Відповідь: .

3.27. При яких рівняння має чотири розв’язки?

Розв’язання:

Розглянемо два випадки.

1) . Маємо: , де . Корені рівняння повинні бути додатними, тому та їх добуток повинен бути менше 1, тобто , звідки .

2) . Маємо: , де . Воно має два розв’язки, якщо .

Відповідь: .

Б. Розташування коренів квадратичної функції відносно заданих точок.

В задачах пункту А на визначення знаків коренів квадратичної функції ми з’ясовували питання про розташування коренів відносно точки . Такий підхід припускає природне узагальнення: не зосереджувати увагу лише на точці і , більш того, піти далі, не обмежуючись тільки цією точкою. Для подібних задач характерна наступна умова: при яких значеннях параметра корені (тільки один корінь) більше (менше, не більше, не менше) заданого числа ; корені розташовані між числами і ; корені не належать проміжку з кінцями в точках і та ін.

З першого погляду здається природним, знайшовши корені квадратичної функції (якщо вони існують), порівняти їх з заданими числами (числом). Відмітимо, що цей шлях виправданий лише в тих випадках, коли нам пощастить – дискримінант квадратичної функції буде повним квадратом. Саме з такого «комфортного» типу задач ми і розпочнемо.

3.28. При яких корені квадратного тричлена більше -2, але менше 0?

Розв’язання:

Дискримінант квадратного тричлена і його корені . Оскільки , то достатньо вимагати, щоб . Крім того, при маємо один корінь, що задовольняє умову.

Відповідь: або .

3.29. При яких будь-який розв’язок нерівності буде також розв’язком нерівності ?

Розв’язання:

Розв’язки першої нерівності знаходимо із сукупності розв’язків двох систем: .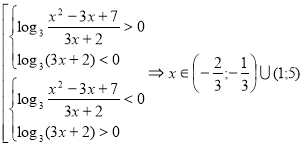

Розглянемо нерівність: . Корені відповідного квадратного тричлена: . Якщо , то умова задачі, очевидно, не виконується, бо . Залишається вимагати, щоб .

Відповідь: .

3.30. З’ясувати, для яких дійсних всі розв’язки нерівності є одночасно розв’язками нерівності .

Розв’язання:

Розв’язки першої нерівності знаходимо з сукупності систем: .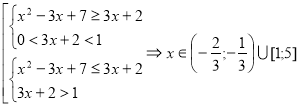

Розглянемо нерівність . Дискримінант квадратного тричлена . Розв’язки нерівності . Необхідно, щоб або   або .

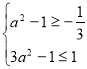Відповідь: або або .

3.31. При яких значеннях параметра має розв’язки система нерівностей ?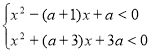

Розв’язання:

Дискримінанти відповідних квадратних тричленів та відповідно. Якщо , то маємо - перетину немає. Якщо , то маємо - перетину немає. Якщо , то . Перетин буде при .

Відповідь: .

3.32. Знайти всі значення параметра , для кожного з яких існує тільки одне значення , яке задовольняє систему рівнянь .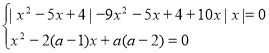

Розв’язання:

Розв’язання першого рівняння спряжене не більше ніж з технічними труднощами. Тому обмежимось лише результатом: або .

Розв’язком другого рівняння будуть . Необхідно, щоб одне з чисел або дорівнювало -1, а інше не потрапляло б до множини . Це можливо при . Далі, якщо , то необхідно, щоб або навпаки.

або .

Відповідь: або або .

3.33. Знайти всі значення параметра , при яких один з коренів рівняння буде більше 3, а інший менше 3.

Розв’язання:

Зробимо заміну .

Переформулюємо задачу. Знайти всі , при яких число 3 лежить між коренями рівняння .

Як і в попередніх задачах пошук коренів квадратичної функції пов’язаний зі знаходженням дискримінанта. Отже, . Оскільки в умові є пряма вказівка на існування двох різних коренів , то дискримінант додатній. Нехай - корені квадратного рівняння, причому . Тоді шукані значення знайдемо, розв’язавши систему 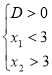. Зрозуміло, що розв’язання цієї системи пов’язано з великими технічними труднощами. Тому для цієї задачі вибраний підхід не виправданий.

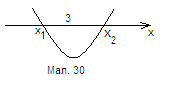Раціональний шлях розв’язання базується на простій геометричній інтерпретації. Позначимо ліву частину рівняння через . Парабола повинна перетнути вісь абсцис в двох точках, причому вона спрямована догори. Тоді малюнок 30 – переклад умови на графічну мову. Тепер треба знайти аналітичне співвідношення, яке буде описувати цю картинку. Неважко здогадатись, що вимога є і необхідною і достатньою умовою для виконання нерівності . Маємо , звідки . Повернемося до підстановки. або .

Відповідь: або .

Дуже корисно узагальнити розібрану задачу, тобто знайти умови, при яких число лежить між коренями квадратичної функції . Звернемось 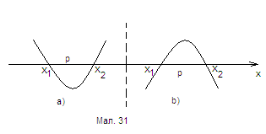знову ж таки до геометричної ілюстрації.  Оскільки з умови випливає, що , то в залежності від знака достатньо розглянути два випадки (мал. 31). Кожен з них описується такими умовами: для a) ;

для b) . Відмітимо, що немає необхідності вимагати виконання умови : нерівності системи гарантують існування двох коренів. Оскільки сукупність цих двох систем рівносильна нерівності , то можна стверджувати наступне:

Твердження 1. Для того, щоб число знаходилось між коренями функції , необхідно і достатньо, щоб виконувалась нерівність .

Після цього буде природним спробувати побудувати критерій, який забезпечить положення заданого числа поза кореневим проміжком. Знаходимо умови, при яких корені квадратичної функції будуть менше числа . Для цього достатньо описати малюнки 32, 33. Легко здогадатись, що вимога забезпечить положення числа поза кореневим проміжком. Зрозуміло, що цієї вимоги недостатньо: при точка може опинитись лівіше кореня або при . Остаточно зафіксує точку в потрібному положенні нерівність , де . Отже, наступна система повністю описує мал. 32. .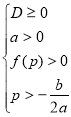

Проводячи такі ж міркування для мал. 33 маємо: 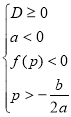. Це і є необхідна і достатня умова того, що число більше коренів квадратичної функції. Сформулюємо його в такому вигляді:

Твердження 2. Для того, щоб число було більше коренів квадратичної функції необхідно і достатньо виконання наступної системи нерівностей .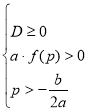

Зробимо декілька зауважень.

1. Якщо в останній нерівності системи поміняти знак 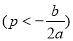, то отримаємо критерій того, що число 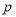буде менше коренів квадратичної функції .
2. Непогано б було пам’ятати твердження 1 і 2. Але спеціально їх запам’ятовувати непотрібно. Головне зрозуміти механізм виникнення необхідних нерівностей і навчитись застосовувати його на конкретних задачах.
3. Очевидно, що твердження 1 і 2 не описують всі задачі, пов’язані з розташуванням коренів квадратичної функції. Так, в великій кількості задач число 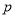може співпадати з одним з коренів. Крім того, отримані критерії сформульовані лише для однієї точки. Але існує великий клас задач на дослідження положення коренів відносно двох (а можливо і більшої кількості) точок або відносно заданого відрізка. Зрозуміло, що для кожного типу прикладів можна побудувати свій критерій. Але навряд чи треба це робити: основна ідея буде повторюватись, а відповідно, простіше не будувати загальну теорію, а вчитись розв’язувати задачі на конкретних прикладах.

 3.34. При яких корені рівняння задовольняють умови ?

Розв’язання:

Вершина параболи має абсцису , яка належить відрізку . Дискримінант квадратного тричлена повинен бути невід’ємним. Старший коефіцієнт більше нуля. Маємо систему: .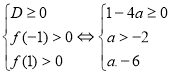

Відповідь: .

3.35. Нехай квадратне рівняння має корені . Знайти всі , що задовольняють умови .

Розв’язання:

Умова задачі описується такими системами нерівностей:

- відповідна квадратична функція.

1) 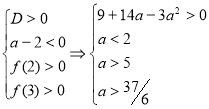       2) .

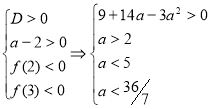Перша система розв’язків немає. Для першої нерівності другої системи маємо: , тому

Відповідь: .

3.36. Нехай квадратне рівняння має корені . Знайти всі такі, що задовольняють умови .

Розв’язання:

Записуємо відповідні системи (які отримаємо за допомогою все того ж графічного образу).

1)

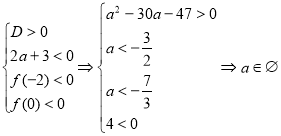
2) .

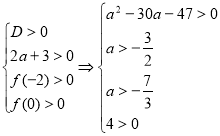Зауважимо, що остання нерівність другої системи означає, що для будь-яких . Перша нерівність має розв’язки: та . Порівнюємо . Оскільки , то .

Відповідь: або .

3.37. При яких корені рівняння задовольняють умову ?

Розв’язання:

Як і в попередніх прикладах записуємо системи:

1) 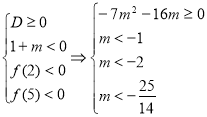     або   2)  .

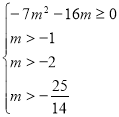Відповідь: або .

3.38. Знайти всі , для яких всі розв’язки нерівності знаходяться в розв’язках нерівності .

Розв’язання:

Можливі три варіанти, які зображено на мал. 34.

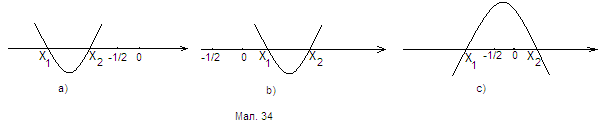
a) 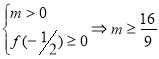;  b) ;   c) .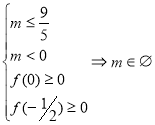

Відповідь: .

В. Задачі, які зводяться до дослідження розташування коренів квадратичної функції.

Цей заголовок достатньо повно відображає основну ідею розв’язування прикладів даного пункту. Треба лише додати, що вміння помітити «замасковану» в задачі квадратичну функцію – прийом достатньо поширений і в великій мірі ефективний. Відмітимо ще, що в цьому пункті зберігаються позначення: - квадратична функція; - дискримінант; - вершина параболи.

3.39. При яких система рівнянь 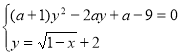  має розв’язки?

Розв’язання:

З другого рівняння системи випливає, що . Тому, якщо хоча б один корінь першого рівняння буде не менше 2, то дана система має розв’язки. Якщо , то . Отже, входить до відповіді. Якщо , то квадратне рівняння зручно записати у вигляді: . Для нього . Якщо , то , тому також входить до відповіді. Якщо , тобто , то шукані значення параметра визначаються сукупністю 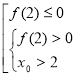. (Неважко побудувати відповідну картинку).

Відповідь: .

3.40. Знайти множину всіх , для кожного з яких рівняння має два корені різних знаків.

Розв’язання:

Піднесемо дане рівняння до квадрату (враховуючи, звичайно, що ). . Останнє рівняння має розв’язки , звідки . Залишається виконати умову або .

Відповідь: або .

3.41. При яких значеннях нерівність не має дійсних розв’язків?

Розв’язання:

Для зручності покладемо . Нерівність не має дійсних коренів в таких випадках:

По-перше, якщо дискримінант квадратичної функції недодатній. .

По-друге, якщо рівняння має від’ємні корені. Це можливо, якщо 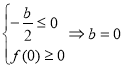. Повертаємось до параметра . .

Відповідь: .

3.42. Знайти , при яких всі розв’язки рівняння задовольняють умову .

Розв’язання:

При маємо , тобто не є коренем цього рівняння. Поділимо дане рівняння на і зробимо заміну . Маємо: , яке має корені . Тоді або . Для першого рівняння для всіх . Необхідно: .

Для другого рівняння . Він невід’ємний при або . Таким чином, - розв’язок, тому що в цьому випадку дане рівняння має два дійсні корені. Далі, необхідно, щоб .

Відповідь: .

3.43. При яких дійсних значеннях рівняння не має дійсних розв’язків?

Розв’язання:

Знаходимо дискримінант квадратичної функції . Якщо , то рівняння розв’язків не буде мати. . Для дане рівняння не буде мати розв’язків, якщо .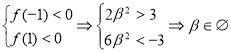

Відповідь: .

3.44. При яких дійсних значеннях параметра рівняння має хоча б один розв’язок?

Розв’язання:

Необхідно, щоб дискримінант квадратичної функції був невід’ємним. . Оскільки , то необхідно, щоб один з коренів квадратичної функції належав відрізку . Вершина параболи належить проміжку . для всіх , отже на корінь є завжди.

Відповідь: або .

3.45. При яких нерівність виконується для всіх ?

Розв’язання:

Зробимо перетворення . Нехай . Оскільки , то . Маємо: . Необхідно, щоб відрізок належав кореневому проміжку квадратичної функції. .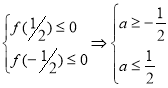

Відповідь: .

3.46. Знайти , при яких нерівність не має розв’язків.

Розв’язання:

При маємо: - розв’язку немає. Далі . Знаходимо дискримінант квадратичної функції. . При дискримінант від’ємний, старший коефіцієнт додатній, отже, розв’язків немає. Якщо , маємо (мал. 35) три можливих положення вершини.

Для першого положення , для другого , для третього .                В останньому випадку необхідно, щоб . Маємо: .

При картинка буде подібною і отримаємо аналогічний результат.

Відповідь: .

3.47. Знайти , при яких нерівність має скінчену кількість розв’язків і вказати ці розв’язки.

Розв’язання:

Зробимо заміну , де . Неважко помітити, що при рівняння має скінчену кількість розв’язків. Тому знайдемо всі , при яких система 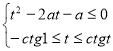має скінчену кількість розв’язків. Очевидно це можливо лише тоді, коли вона (система) має рівно один розв’язок. Якщо дискримінант відповідного квадратного тричлена від’ємний, то система розв’язків немає. Якщо , тобто або , то розв’язком першої нерівності буде лише точка . З двох значень параметра підходить лише , бо . Звідки . З умови маємо: .

Якщо , то розв’язком нерівності буде міжкореневий проміжок , який повинен мати тільки одну спільну точку з відрізком . Звідки або . Тоді шукані значення параметра знайдемо, розв’язавши наступну сукупність систем: 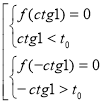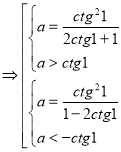. Легко переконатися, що друга система розв’язків немає. З першої системи при знайденому знаходимо . Тоді або .

Відповідь: якщо , то ; якщо , то .

3.48. Знайти всі дійсні значення , для яких при всіх існують в проміжку розв’язки рівняння .

Розв’язання:

Оскільки , то , а . Зробимо заміну , маємо . Тепер зрозуміло, що треба знайти такі , для яких при всіх рівняння має хоча б один корінь в інтервалі .

Покажемо на цьому прикладі, який вже можна назвати «стандартним», як, використовуючи конкретні властивості задачі, скоротити технічну роботу. Так, абсциса вершини параболи додатна . Отже, при рівняння не має коренів на проміжку . Далі, при , знову ж таки, завдячуючи тому, що , більший корінь рівняння завжди додатній. Тому залишається розглянути випадок, коли менший корінь належить проміжку . Маємо: 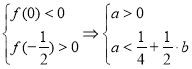. Оскільки друга нерівність повинна виконуватись для всіх , то .

Відповідь: .

3.49. Знайти , при яких існують розв’язки системи .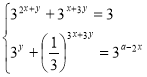

Розв’язання:

Помножимо друге рівняння системи на , отримаємо: 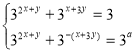. Нехай ;, тоді 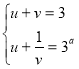. Віднімаючи від першого рівняння друге, дістанемо: . Вимога єдиності розв’язку вихідної системи може бути приводом для того, щоб вимагати те саме від отриманого квадратного рівняння. Але, коли маємо подібну ситуацію, важливо не випустити, що в результаті заміни значення нової змінної можуть бути обмежені якою-небудь множиною. Тому питання про кількість розв’язків повинно бути безпосередньо пов’язане з цією множиною. Так, в даній ситуації , . Разом з тим, . Тоді, з урахуванням останньої системи, . Таким чином, треба знайти значення параметра, при яких рівняння має єдиний розв’язок для . Зрозуміло, що . Вимоги знаходимо з сукупності систем: .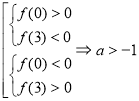

Відповідь: .

3.50. При яких значеннях параметра нерівність виконується для всіх дійсних ?

Розв’язання:

Зробимо заміну . Необхідно знайти всі , для яких нерівність виконується для всіх . Маємо сукупність систем: 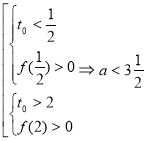або . Крім того, (це очевидно) нерівність виконується за умови .

Відповідь: .

3.51. При яких значеннях параметра нерівність виконується для всіх дійсних ?

Розв’язання:

Зробимо заміну , при цьому . Зрозуміло, що необхідно, щоб . Якщо , то умова задачі виконується. Звідки - розв’язок. Якщо , то необхідно виконання умов .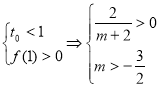

Відповідь: .