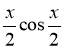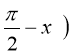Конспект уроку з алгебри та початків аналізу за підсумковим повторенням "Розв'язання тригонометричних рівнянь"

1.Маховикова Лариса Миколаївна

2.Криворізька загальноосвітня школа І-ІІІ ступенів № 117

3. На уроці вчителем було заплановано отримати такі навчальні результати: знати: означення обернених тригонометричних функцій, основні формули для розв’язування  тригонометричних рівнянь; формули тригонометрії; способи розв’язування  однорідних тригонометричних рівнянь першого ступеня, другого ступеня; графічне зображення розв’язків тригонометричних рівнянь і нерівностей; уміти: обчислювати обернені тригонометричні функції деяких  числових значень; розв’язувати найпростіші  тригонометричні рівняння та ті, шо зводяться до них, а також застосовувати тригонометричні  перетворення до більш складних; відображувати  розв’язання  на одиничному колі, сприймати  усну мову, брати участь у діалозі; приміняти: отримані  знання до розв’язування тригонометричних рівнянь різної складності,  вивчення формул перетворення  тригонометричних виразів, необхідних при  розв’язуванні   рівнянь. За допомогою інтерактивної дошки вчитель може активізувати роботу учнів, передбачити їх відповіді, покроково пояснити хід  розв’язування нових типів рівнянь.

Конспект уроку з алгебри та початків аналізу за підсумковим повторенням

у 11 класі

Тема: «Розв’язування тригонометричних рівнянь»

Мета:

• навчальна: систематизувати знання учнів по темі: «Тригонометричні рівняння»; надати допомогу у вдосконаленні навичок у розв’язуванні найпростіших тригонометричних рівнянь. Побудувати алгоритм дій при   розв’язуванні тригонометричних  рівнянь.
• развивальна: Сприяти розвитку вмінь порівнювати, узагальнювати, класифікувати, аналізувати, робити висновки;

виховна: Заохочувати учнів до само і взаємоконтролю, виховувати пізнавальну активність, самостійність, наполегливість у досягненні цілей, розвивати комунікативні вміння, рефлексію, культуру та дисципліну розумової праці.

Універсальні навчальні дії (УНД): особистнісні: формування стійкої мотивації до навчання на основі алгоритма виконання завдань; регулятивні: оцінювання вірності виконання дій на рівні адекватної ретроспективної оцінки; пізнавальні: здійснювання пошуку необхідної інформації для виконання навчальних завдань з використанням навчальної літератури; комунікативні: враховування різних думок та прагнення до координації різних позицій у співпраці.

Заплановані навчальні результати: знати: означення обернених тригонометричних функцій, основні формули для розв’язування  тригонометричних рівнянь; формули тригонометрії; способи розв’язування  однорідних тригонометричних рівнянь першого ступеня, другого ступеня; графічне зображення розв’язків тригонометричних рівнянь і нерівностей; уміти: обчислювати обернені тригонометричні функції деяких  числових значень; розв’язувати найпростіші  тригонометричні рівняння та ті, шо зводяться до них, а також застосовувати тригонометричні  перетворення до більш складних; відображувати  розв’язання  на одиничному колі, сприймати  усну мову, брати участь у діалозі; приміняти: отримані  знання до розв’язування тригонометричних рівнянь різної складності,  вивчення формул перетворення  тригонометричних виразів, необхідних при  розв’язуванні   рівнянь; отримана компетентність: цілісна

Обладнання:

• таблиці
• завдання на друкованій основі;
• зошити для самостійних робіт;
• проектор;
• інтерактивна дошка (малюнки до уроку № 1).

УРОК № 1  «Розв’язування найпростіших тригонометричних рівнянь »

ХІД УРОКУ

1. Організаційний момент.

Дані рівняння можуть бути присутніми у завданнях І , ІІ та ІІІ рівнів  на ЗНО. У завданнях І рівня зазвичай пропонуються найпростіші  рівняння чи завдання, в яких,  застосовуються основні способи розв’язування. У ІІ рівні  необхідно використовувати  різні  методи розв’язування рівнянь. В завданнях ІІІ рівня розв’язання  тригонометричного рівняння являє собою один з етапів   розв’язання показникового, логарифмічного рівнянь  чи дослідження функції.

2. Актуалізація знань, вмінь та навичок учнів.

До найпростіших    тригонометричних  рівнянь відносяться  рівняння :

sin x = a, cos x = a, tg x = a, ctg x = a

Повторення матеріалу проводиться за таблицею 

Арксинусом числа а називається число b, b [– ; ], sin b = a

Арккосинусом числа а називаеться число b, b [0; π], cos b = a

arcsin(– a) = – arcsinа;         arccos (–a) = π – arccosa;

arctg(– a) = – arctga;            arcctg(– a) = π – arcctga.

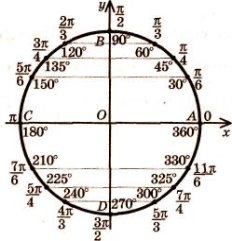
Тригонометричний круг: (інтерактивна дошка)

III. Реалізація мети уроку.

Усно. Розв’язати  рівняння: 1) sin х= 1;

2) cos x = ; 3) cos x = – ; 4) sin х = ; 5) tg х = 1; 6) сtg х = ; 7) сtg х = – 3;

Письмово:

Завдання 1. Розв’язати  рівняння :  8) sin х =

Розв’язання:   х = (– 1)^k arcsin + π k, k Z;   х = (– 1)^k + πk k Z.

 Відповідь: х = (– 1)^k + πk,  kZ.

Робота в парах: (через проектор) Учні в парах обмінюються  зошитами і проводять взаємоперевірку.

Відповіді: 9) х = ; 10) х =k, kZ; 11) х = k, kZ; 

12) х = ; 13) х = ; 14) х = ; 15) х = ; 16) х = ; 17) х = .

Іноді в тестах ЗНО до завдань додаються додаткові питання. Розглянемо деякі з них на прикладі завдання №1 (рівняння  8). При відповідях на додаткові  питання  зручно представити розв’язання в вигляді об’єднання двох сімейств  розв’язків

х = + 2πk, kZ (1)      х = + 2πn, nZ (2).

Додаткові питання   (проектор)

А) Знайти найменший додатній корінь.

Вибираємо найменший додатній розв’язок із кожоого сімейства. Із (1) маємо х = , із (2)  х = . Найменшим з них буде .       Відповідь: або 60°.

Б) Знайти  найбільший  від’ємний корінь.

При k = – 1 з (1) маємо х = – 2πk = - .

При n= – 1 з (2) маємо х = – 2π = – .

 Найбільший з них буде – .                                 Відповідь: – або – 240°.

В)  Знайти ті корені рівняння, для яких cos х > 0

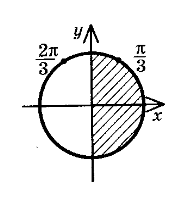Відмітимо усі розв’язки рівняння (1) на тригонометричному колі. Із цих розв’язків необхідно вибрати ті, для  яких cosx > 0.  Відомо, що cos х > 0, якщо х лежить у I чверті або у IV чверті.  Отримуємо, що

х = + 2πk, k Z                        Відповідь : + 2πk, k Z.

Г)  Вказати ті корені, які  належать  проміжку

[–3π; – π]

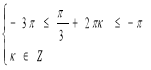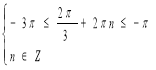 Розв’яжемо системи (1)  і (2).

 Маємо (1) 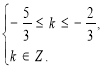k = – 1 і х = – .

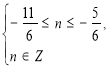
(2) n= – 1 і х = –.                             Відповідь: – ; – .

Д) Скільки коренів має рівняння на проміжку [–3π; ]?

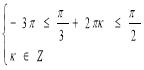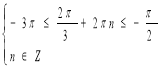 Розв’яжемо системи (1)  і (2).

Розв’язком  (1) системи буде k = – 1 і k = 0. Р Розв’язком (2) системи буде n= – 1.

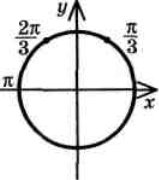Таким чином, отримуємо 2 + 1 = 3 кореня.     Відповідь: 3 кореня

Е) Знайти найближчий до π корінь рівняння.

 Відмітимо всі корені рівняння (I) на тригонометричному колі

 Шуканим коренем є .

 Відповідь:.

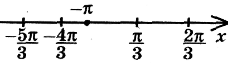Є) Між  якими  коренями знаходиться число – π ?

Відмітимо корені рівняння (1) на координатній прямій.

 Відповідь: – < – π < .

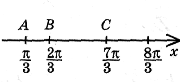Ж) Знайти найбільшу довжину відрізка, у якому не  знаходиться жодного кореня рівняння.

Відмітимо корені рівняння (1) на координатній прямій.

Серед  відрізків АВ чи ВС необхідно вибрати найбільший. Довжина АВ дорівнює  – = . Довжина ВС дорівнює – = . Найбільша довжина дорівнює .                                    Відповідь : .

З) Знайти найменшу довжину відрізка, на  якому знаходяться два кореня рівняння.

Відмітимо корені рівняння (1) на координатній прямій .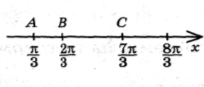

Серед  відрізків АВ чи ВС необхідно вибрати  найменший.

Довжина АВ дорівнює – = . Довжина ВС дорівнює – = . Найменша  довжина дорівнює .                                      

 Відповідь : .

IV. Запис домашнього завдання, та його аналіз:

повторити § 21 (формули!)

 № 12, 13;

V. Підсумки  урока: 

1.Оцінки.

2. Звернути увагу на теоретичний матеріал у таблицях, що використовувалися на уроці.