Міністерство освіти і науки України

Департамент освіти і науки Кіровоградської облдержадміністрації

Кіровоградська Мала академія наук учнівської молоді

Гайворонська філія Кіровоградської Малої академії наук учнівської молоді

 

 

 

 

Відділення: математика Секція: математика

 

 

 

ФРАКТАЛи ТА ЇХ ПРАктичне застосування

 

 

 

 

Роботу виконав: Коваль Ростислав Юрійович, учень 9 класу  загальноосвітньої школи  І-ІІІ ступенів села Хащувате Гайворонського району  Кіровоградської області   Вчитель: Новіцька Галина Василівна, вчитель математики загальноосвітньої школи І-ІІІ ступенів села Хащувате Гайворонського району  Кіровоградської області   Керівник секції: Гречана Віра Василівна, вчитель математики НВК "Гайворонська гімназія-загальноосвітня школа І-ІІІ ступенів № 5"

 

 

 

 

 

 

 

 

Гайворон – 2015

ТЕЗИ

 

Науково – дослідницька робота « Фрактали та їх застосування» учня 9 класу загальноосвітньої школи І – ІІІ ступенів с. Хащувате Гайворонського району Кіровоградської області, слухача Гайворонської філії Кіровоградської Малої академії наук Коваля Ростислава Юрійовича.

Науковий керівник: Гречана Віра Василівна, вчитель математики НВК "Гайворонська гімназія-загальноосвітня школа І-ІІІ ступенів № 5».

Вчитель: Новіцька Галина Василівна, вчитель математики загальноосвітньої школи І-ІІІ ступенів села Хащувате Гайворонського району Кіровоградської області

Об’єктом дослідження – є  фрактали.

Мета роботи – вивчення теоретичних питань з даної теми та аналіз застосування фракталів у різних галузях науки.

Актуальність дослідження: оскільки фрактальна наука ще досить молода, то вона майже не відома широкому загалу, але через здатність описувати предмети та явища – тобто все, що нас оточує з точністю до найдрібніших  деталей, вона є дуже перспективним напрямком науки. Тому, ця тема є дуже актуальною.

Фрактали займають досить важливе і визначальне місце в комп’ютерній графіці. По-перше - побудова ландшафтів, дерев, рослин, навіть тварин і генерування фрактальних текстур і по друге -  це фрактальне стиснення зображень. Сучасна фізика і механіка тільки - тільки починають вивчати поведінку фрактальних об'єктів. І звичайно, що фрактали застосовуються безпосередньо в самій математиці.

   В основі роботи лежать фрактали – дивно красиві і таємничі геометричні об’єкти, що були відкриті більше 40 років тому. 

У моїй роботі  приділено основну увагу різним визначенням фракталів, класифікації фракталів, дослідникам цього напряму науки,  зв'язку фракталів з природою і мистецтвом.

Мета, задачі дослідження:

• Зрозуміти, що таке фрактал;
• Визначити  основні види фракталів;
• З'ясувати, в яких областях науки і техніки використовуються фрактали.

 Перевірити  чи існує зв'язок між фракталами і :

трикутником Паска ля;  фігурними числами; літературними творами.

Завдання дослідження :

• Опрацювати і проаналізувати літературу по темі дослідження.
• Розглянути різні  види фракталів, їх класифікацію.
• Зібрати колекцію фрактальних образів для первинного ознайомлення зі світом фракталів.
• Встановити взаємозв'язки між  трикутником Паскаля, літературними творами, фігурними числами.

Методи  дослідження :

- теоретичний (вивчення і теоретичний аналіз наукової і спеціальної літератури;  узагальнення досвіду);

- практичний ( складання розрахунків, узагальнення результатів)

Наукова новизна одержаних результатів.

  Дізнався в яких областях науки і техніки використовуються фрактали.

Встановлений зв’язок між фракталами  і трикутником Паскаля, літературними  творами, фігурними числами.

Практичне значення одержаних результатів.

Роль фракталів сьогодні досить велика і значна. Вони приходять на допомогу, коли потрібно за допомогою декількох коефіцієнтів задати лінії і поверхні дуже складної форми. Фактично, знайдений спосіб допомогає знайти зв'язок між фракталами та іншими галузями науки.

 Ця тема дуже цікава і змістовна, розвиває пізнавальний інтерес до математики. Дуже сподіваюся, що ця робота принесе користь  і  ровесникам, і старшокласникам, і вчителям. Історія математики повна несподіваних і цікавих фракталів, і дуже часто їх розв’язок служив поштовхом до нових відкриттів, з яких, у свою чергу, зростали нові фрактали.

 

 

ЗМІСТ

 

ВСТУП………………………………………………………………………..	5
РОЗДІЛ 1.ФРАКТАЛ.ІСТОРІЯ ЙОГО ВИНИКНЕННЯ. КЛАСИФІКАЦІЯ ФРАКТАЛІВ………………………………………………………………..	6
1.1. Історія виникнення фракталу …………………………………….	6
1.2. Види фракталів та методи їх створення……………………………….	9
1.3.Типи самоподібності у фракталах……………………………………...	10
1.4 Розмірність фракталів…………………………………………………...	11
1.5. Класифікація фракталів………………………………………………...	12
1.5.1.Геометричні фрактали. …………………………………......................	12
1.5.2.Алгебраїчні фрактали………………………………………………….	15
1.5.3. Стохастичні фрактали ………………………………………………..	15
1.6. Об’єкти, що володіють фрактальними властивостями,    в  природі..	16
РОЗДІЛ 2. ЗНАХОДЖЕННЯ ФРАКТАЛЬНОЇ СТРУКТУРИ У ТРИКУТНИКУ ПАСКАЛЯ, ФІГУРНИХ ЧИСЛАХ, ЛІТЕРАТУРНИХ ТВОРАХ …………..................	20
2.1. Трикутник Паскаля……………………………………………………..	20
2.2. Фігурні числа……………………………………………………………	21
2.3. Літературні твори……………………………………………………….	24
ВИСНОВКИ …………………………………………………………………	27
ЛІТЕРАТУРА………………………………………………………………..	28
ДОДАТКИ……………………………………………………………………	29

 

ВСТУП

У сучасному світі все швидко змінюється. Це стосується і найстарішої науки - математики. На уроках геометрії ми вивчаємо кола, паралелограми, трикутники, квадрати і т.д. Проте природа багата на «неправильні» об’єкти, що зазнали впливу різних явищ. У своїй книзі «Фрактальна геометрія природи» Б. Мандельброт  наголошує увагу на  наступну думку: «Чому геометрію часто називають «холодною» та «сухою»? Одна з причин полягає в її непристосованості описувати форму хмари, гори, берегової лінії або дерева. Хмари - не сфери, гори - не конуси, берегові лінії - не кола, деревна кора не гладка, а блискавка поширюється не по прямій. У більш загальному плані я стверджую, що багато об'єктів у природі настільки іррегулярні (від латинського неправильний, не підпорядкований певному положенню, порядку) і фрагментовані, що в порівнянні з Евклідом - термін, який в цій роботі означає всю стандартну геометрію, - природа володіє не просто більшою складністю, а складністю зовсім іншого рівня. Число різних масштабів довжин природних об'єктів для всіх практичних цілей нескінченно». [5, с. 25].  Фрактали – це  область незвичного математичного мистецтва, коли при допомозі простих формул і алгоритмів можна утворити картини надзвичайної краси і складності! У контурах побудованих зображень часто можна побачити щось схоже на листя, дерева і квіти.

Робота складається із вступу, 2 розділів, висновку та списку використаних джерел. Кожен розділ побудовано за наступною структурою. На початку розділу наводиться необхідний теоретичний матеріал, потім викладено задачі з докладним розв’язанням побудови фракталів: «Сніжинка Коха», «Килим Серпінського». В першому розділі роботи “Фрактал. Історія його виникнення. Класифікація фракталів” дано тлумачення терміну «фрактал»; історія виникнення фракталів; біографія засновника фрактальної геометрії -  Бенуа Мандельброта. Знайомство з геометричними фракталами, алгебраїчними, стохастичними. У другому розділі з’ясовуємо, що існує зв’язок між фракталами і трикутником Паскаля, фігурними числами та літературними творами.

РОЗДІЛ 1. 

ФРАКТАЛ. ІСТОРІЯ ЙОГО ВИНИКНЕННЯ. КЛАСИФІКАЦІЯ

 ФРАКТАЛІВ

 

 

1.1.          Фрактал. Історія його виникнення.

Все, що створила людина і природа  обмежено площинами. Коли ми зустрічаємо об’єкт у природі, то спочатку звертаємо увагу на те, що описати його форму можна лише наближено та нечітко і допоможуть нам  у цьому фрактали. Фрактали зустрічаються там, де закінчуються правильні форми Евклідової геометрії. Фракта́л (лат. fractus — подрібнений, дробовий) – нерегулярна, самоподібна

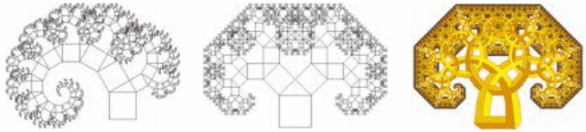
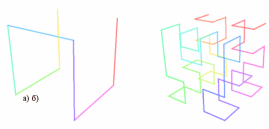
           рис.1.1                                        структура. Фрактал – це малюнок, що складається з подібних (ідентичних) між собою елементів.   У широкому розумінні фрактал означає фігуру, малі частини якої в довільному збільшенні є схожими до неї самої. (рис.1.1) Фрактали досліджувалися ще задовго до того , як їм було привласнено ім’я. Наприклад, в етноматематиці, в роботі Рона Еглаша «Африканські Фрактали» було задокументовано поширеність фрактальних геометричних фігур тубільців. Альберхт Дюрер – німецький художник,  у 1525р. опублікував свою роботу – «Керівництво художника» і один із його численних розділів має назву «Черепичні шаблони, утворені пентагонами». Пентагон Дюрера був дуже схожий на килим Серпінського, та він використовував не квадрати , а п’ятикутники, що теж є прикладом застосування фракталів. Також Джексон Поллок - американський експресіоніст 50-тих років відтворював на полотні  об'єкти, що були схожими на фрактали. Вільгельм Лейбніц – німецький філософ, математик зробив великий внесок у розвиток фракталів. Саме ця людина є розробником ідеї так званої «рекурсивної самоподібності» У 1872 Карл Веєрштрасс знайшов приклад функції з неінтуїтивною особливістю, скрізь неперервної, але ніде недиференційованої — графік цієї функції тепер називався б фракталом. У 1904році  шведський вчений Хельге Фон Кох, незадоволений занадто абстрактним і гострим означенням Веєрштрасса, розробив більш геометричне означення тієї самої функції. Він придумав безперервну криву, яка ніде не має дотичної, але найголовніше те, що її дуже просто намалювати. Після цього вчені вияснили, що вона має властиловості фрактала, бо в ній використовується ітерація. Цей фрактал зараз має назву  «сніжинка Коха». Пол П'єр Леві далі розвинув ідею самоподібних кривих, які складаються із частин, подібних до цілого. Француз  у своїй роботі «Криві та поверхні на площині та у просторі», виданій 1938 року, описав нову, ще досі невідому загалу  фрактальну криву, яка зараз відома під назвою «Крива Леві» (рис.1.2 а, б, в).

               а)                                          б)                                       в)

Рис.1. 1

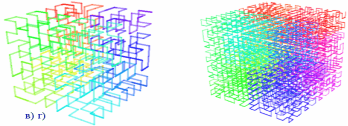
Ґеорг Кантор навів приклади підмножин дійсних чисел із незвичайними властивостями — ці множини Кантора тепер також вважаються за фрактали. Анрі Пуанкаре, Фелікс Кляйн, П'єр Фату та Ґастон Жюліо досліджували ітераційні властивості на комплексній площині в кінці XIX та на початку XX століття. Але через брак сучасного комп’ютерного обладнання у них не вистачило засобів

Рис.1.3

відобразити красу і новизну багатьох із відкритих ними об'єктів.

У 1975 році Мандельброт використав слово «фрактал», як назву для об'єктів Хаусдорфа, розмірність яких є більшою за топологічну розмірність, наприклад Крива Гільберта (рис.1.3 а,б,в,г). Після цього такі об’єкти і отримали свою теперішню назву.

Бенуа Мандельброт (фр. Benoît Mandelbrot )(20 листопада 1924 — †14 жовтня 2010) — французький математик польського походження, засновник фрактальної геометрії. Його ім'я відоме багатьом у зв'язку з фракталом, названим на його честь, — множиною Мандельброта. Математик також займався економікою, теорією інформації, космологією та іншими науками, тобто проводив дослідження у різних галузях науки. Мандельброт став лауреатом премії Вольфа з фізики у 1993 році, Японської премії за інноваційні ідеї в науці у 2003 році та власником численних нагород.

      Бенуа Мендельброт народився у єврейській родині у Варшаві в 1924 році. Але вже у 1936 році родина Бенуа емігрувала у Францію, в Париж. У Парижі він потрапив під вплив свого дядька Шолема Мандельброта, відомого паризького математика, члена групи математиків, відомії під загальною назвою «Ніколя Бурбакі» викладача престижного паризького навчального закладу  - Колеж де Франс.

Після початку війни Мандельброти переїхали на південь Франції, у  мальовниче містечко Тюль, Бенуа навчався у школі. У нього відкрився незвичайний математичний дар, який дозволив йому після війни стати студентом відомої Політехнічної школи (1945—1947). Виявилося, що в Бенуа чудова просторова уява. Він навіть алгебраїчні завдання розв'язував геометричним способом. Оригінальність його рішень дозволила Мандельброту вступити до університету.

Після Політехнічної школи у 1947—1949 р.р. Бенуа вивчав аеронавтику у Каліфорнійському технологічному інституті. Він захистив докторську дисертацію з математики («Ігри комунікацій») у 1952 в Сорбонні. У 1958 він переїхав у США, де приступив до роботи в науково-дослідному центрі IBM в Йорктауні, оскільки IBM у той час займалася саме цікавими для Бенуа Мандельброта областями математики.

1.2.          Види фракталів та методи їх створення

Фрактали можна створювати різними способами , але серед них можна виділити 3 методи.

Перший метод — ітераційні функції, що будуються відповідно до зазначених правил геометричних заміщень, в результаті яких утворюються геометричні фрактали, наприклад: сніжинка Коха (рис.1.4).

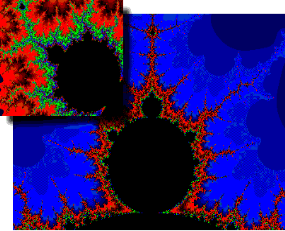
           Рис. 1.4                                                      Рис.1.5

 

 

 

                                                         

 

        Рис.1.6                                                       Рис.1.7

А також множина Кантора, килим Серпінського, трикутник Серпінського, крива Пєано, крива Коха, крива дракона, Т-Квадрат та губка Менгера є прикладами геометричних фракталів.

Другий метод — рекурентні відношення, це фрактали, що визначаються рекурентним відношенням у кожній точці простору (такому як площина комплексних чисел). Отримані таким методом фрактали називають алгебраїчними (рис.1.5.).

Прикладами алгебраїчних фракталів є множина Мандельброта (рис.1.6), палаючий корабель та фрактал Ляпунова.

Третій метод —  це випадкові процеси,  фрактали, що генеруються з використанням стохастичних, а не детермінованих процесів, наприклад: фрактальні ландшафти: гори, дороги, елементи живої природи і т.д., траєкторія Леві та броунівське дерево (рис.1.7).

              

1.3.          Типи самоподібності у фракталах

Класифікація фракталів може відбуватися залежно від  їхньої самоподібності. Роз-різняють три типи самоподібності у фракталах :

  Точна самоподібність – це найсильніший тип самоподібності; фрактал збері-гає однаковий вигляд при різноманітних збільшеннях. У фракталів, згенерованих з використанням ітераційних функцій, майже завжди виявляється точна самоподіб-ність.

  Майже самоподібність – слабка форма самоподібності; фрактал  виглядає

Приблизно ( але не точно) самоподібним при різних його збільшеннях. Майже само-подібні фрактали  містять невеликі копії цілого фракталу у перекручених та вирод-жених формах, тобто при різноманітних крихітних змінах розмірів частинок. Фрак-тали, згенеровані з використанням рекурентних відношень, зазвичай є майже (але не точно) самоподібними.

Статистична самоподібність – це найслабкіша форма самоподібності; фрактал   має чисельні або статистичні міри, що зберігаються при збільшенні.

Найприйнятніші означення «фракталів» просто містять в собі деякий вид ста-тистичної самоподібності (розмірність фракталу, саме по собі, є чисельною мірою, що зберігається при збільшенні). Ймовірні фрактали є прикладами фракталів, які є статистично, але не майже  й не точно самоподібними.

Слід зазначити, що не всі самоподібні об'єкти є фракталами;наприклад, числова вісь (евклідова пряма) є точно самоподібною, але, оскільки її розмірність Гаусдорфа та топологічна розмірність дорівнюють одиниці, вона не є фракталом.

 

1.4.          Розмірність фракталів.

У евклідової геометрії є поняття розмірності: розмірність крапки – нуль, від-різка та кола – одиниця, круга і сфери – два, кулі – три. З одновимірними об’єктами ми пов’язуємо поняття довжини, з двовимірними – площі і так далі. Але як можна уявити собі множину з розмірністю 3/2? Мабуть, для цього потрібно щось проміжне між довжиною і  площею, і якщо довжину умовно назвати 1 – мірою , а площа – 2 – мірою, то потрібно ( 3 / 2) – міра.

 У 1919 році Ф. Хаусдорф дійсно визначив а – міру і на цій основі кожній мно-жині в евклідовому просторі підставив число, назване їм метричною розмірністю. Він же навів перші приклади множин з дробовою розмірністю. Виявилось, що дро-бову розмірність мають Канторівська множина, крива Коха і інші екзотичні об’єкти, до недавнього часу маловідомі за межами математики.

Оскільки фрактал складається з нескінченного числа елементів, що повторю-ються, неможливо точно виміряти його довжину. Це означає, що чим точнішим інструментом ми будемо його вимірювати, тим більшою виявиться його довжина. Тоді як гладка евклідова лінія заповнює в точності одновимірний простір, фрак -тальна лінія виходить за межі одновимірного простору, вторгаючись у двовимірне. Таким чином, фрактальна розмірність кривої Коха знаходитиметься між 1 і 2. Найдивовижнішим виявляється те, що й багато природних об’єктів володіють ніби дробовою розмірністю, хоча, відверто кажучи, для природних об’єктів таку розмір-ність обчислити неможливо. Правильніше сказати, що в певних діапазонах спосте-реження природні об’єкти. Що виникли в результаті довгої дифузії й абсорбції, схожі на фрактальні множини. Наприклад, розмірність побережжя лежить між 1,01 і 1,6, а кровоносної системи людини – між 3,4 і 3,6.

1.5.          Класифікація фракталів

Фрактали поділяються на дві групи :створені науковцями (абстрактні) ; створені  природою ( фізичні).Головна відмінність фракталів, створених людиною і природних фракталів це те, що ті фрактали, які були придумані вченими,  при будь-якому масштабі мають фрактальні властивості. А якщо розглядати природні фрактальні об'єкти, то при більш детальному їх розгляді ми, врешті-решт, підійдемо до масштабу, де починають проявлятися квантові ефекти. Це означає, що природні фрактали не мають субструктур, що нескінченно повторюються, і не можуть демонструвати нескінченну самоподібність. У цьому полягає особливість природних фракталів. Для природних фракталів у класифікаційній таблиці використаний термін - "фізичні фрактали", щоб підкреслити їх «нерукотворність». Фрактали створені вченими також мають класифікацію. Ці фрактали  поділяються  на три групи: геометричні; алгебраїчні; стохастичні.

1.5.1.   Геометричні фрактали

Геометричні (детерміновані, лінійні, прості) фрактали найнаочніші оскільки відразу видно самоподібність. Саме з них почалася історія фракталів. Це і є ті функції-монстри, яких так називали за недиференційованість у кожній точці. У двомірному випадку їх отримують за допомогою деякої ламаної (чи поверхні в тривимірному випадку), званої генератором. За один крок алгоритму кожен з відрізків, складових ламаної, замінюється на ламану-генератор у відповідному масштабі. У результаті нескінченного повторення цієї процедури, виходить геометричний фрактал. У машинній графіці використання геометричних фракталів потрібне при отриманні зображень дерев, кущів, берегової лінії. Двомірні геометричні фрактали використовуються для створення об'ємних текстур (малюнка на поверхні об'єкту). Фрактали цієї групи не лише наочні, але і простіші. [1, с. 62]

Канторівська  множина

Перші ідеї фрактальної геометрії виникли у 19 столітті. Один із найдавніших фракталів - множина Кантора .

Рис.1.8 Побудова Канторівської множини.

План її побудови полягає в наступному.Спочатку береться відрізок прямої одиничної довжини. Потім він поділяється на три рівні частини, і виймається відрізок в середині, що знаходиться між точками  1/3 і 2/3. Це перший крок ітераційної процедури. На другому кроці подібній же процедурі ділення на три рівні частини і наступного видалення середини піддається кожен з двох відрізків, що залишився. Так триває до безкінечності. Легко побачити, що сумарна довжина відрізків дорівнює нулю, оскільки ми виключили в результаті довжину, рівну 1:

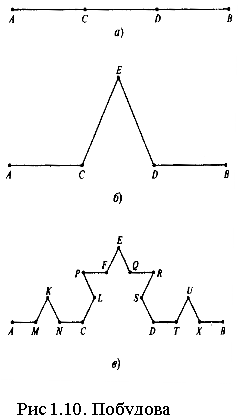
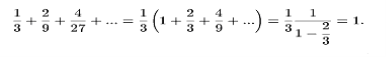
    Отже, виникла множина яка є нескінченним числом ізольованих точок, яке і дістало назву Канторівська множина. (рис.1.8)

 

Рис 1.9. Крива Коха

Ще одним дуже відомим геометричним фракталом є крива Коха, названа так на честь шведського математика Хельги фон Кох, що відкрив її ще в 1904 році. Різновиди цієї кривої дуже часто використовуються при наведенні прикладів по даній темі. Один з найбільш відомих різновидів кривої Коха і буде розглянута далі в моїй роботі.

    Для того, щоб побудувати цей фрактал, треба послідовно виконати нескінченне число кроків. Початковий крок - нульовий. Візьмемо відрізок довільної довжини (Рис.1.10, а) і поділимо його на три рівні частини. На середньому відрізку CD побудуємо правильний трикутник CED, чию основу CD ми потім видалимо. Ми отримаємо криву  ACEDB, у якої усі ланки рівні (Рис.1.10, б).Другий крок: кожна з ланок AC, CE, ED, DB знову поділимо на три рівні частини і побудуємо на середніх відрізках правильні трикутники, чиї підстави ми потім видалимо. Ми отримаємо нову ламану AMKNCLPFEQRSDTUXB (Рис.1.10,в). Другий крок закінчений. Продовжуючи цей процес до безкінечності, ми і отримаємо шуканий фрактал - криву Коха. Як видно на рисунку 6, крива Коха дуже точно імітує сніжинку, тому замкнуту криву Коха називають ще і сніжинкою Коха (Рис. 1.11).

Безумовно, наведені мною приклади геометричних фракталів не є єдиними. Існує ще величезна кількість інших, ще складніших і цікавіших фракталів. Наприклад, дуже цікавою, а тому відомою є крива Гільберта. Початковим елементом є відрізки, твірні криву, схожу на букву "П".У кожному з наведених прикладів ми розглянули декілька послідовних стадій перетворення                                                               початкової фігури. Кожна з отриманих на окремому етапі фігур називається передфракталом, і їх саме подібність  очевидна. Справжній фрактал вийде, якщо число кроків алгоритму побудови прямуватиме до нескінченності.

   Геометричні фрактали мають колосальне практичне значення. Застосовуючи їх в машинній графіці, учені навчилися отримувати складні об'єкти, схожі на природні : зображення сніжинок, гірських вершин, штучних хмар, дерев, кущів, гілок, берегової лінії тощо.

1.5.2.   Алгебраїчні фрактали

Простий приклад алгебраїчних фракталів – це геометрична прогресія 1, 2, 4, 8,16,32,...,2ⁿ,2 ^n +1,.. Якщо відкинути перші три члени, то отримаємо послідовність 8,16,32,...,2ⁿ,2^{n +1},... Це також геометрична прогресія, причому з тим же знаменником. Крім того, її можна отримати з початкової прогресії множенням всіх членів на 8. Вона «подібна» вихідної прогресії з коефіцієнтом 8. залишиться вірним і при відкиданні будь-якого числа початкових членів Звичайно, аналогічний ефект автоподібності. Другий приклад алгебраїчних фракталів – це геометрична прогресія   …, , , , 1, 3,9, 27, … Помноживши кожен член цієї  прогресії на 3, отримаємо послідовність …, , , 1, 3, 9, 27, 81, …, яка виявилася тією ж самою прогресією.

1.5.3.   Стохастичні  фрактали

Третя група – це стохастичні фрактали, при побудові яких у ітеративної системі випадковим чином змінюються будь-які параметри. Термін "стохастичність" походить від грецького слова, що означає "припущення".     Також прикладом випадковості в природі є броунівський рух. За допомогою комп'ютера такі процеси будувати досить просто, тому що він дозволяє генерувати послідовності випадкових чисел. Ці фрактали використовуються при моделюванні рельєфів місцевості і поверхні морів, процесу електролізу.

Ініціатором сніжинки є пряма, а точніше три відрізки прямих, що перетинаються в одній точці (рис. 1.12 а). Для краси і наочності бажано брати відрізки, для яких точка перетину є середина (назву цю фігуру Z). Потім на кінці цих відрізків поміщаємо такі ж фігури Z (рис. 1.12 б, в, г), і робимо це нескінченно. Так ми отримуємо Сніжинку Коха, яка зовні схожа з цією сніжинкою, в цьому є відмінність стохастичних фракталів від інших.

 

 

 

 

 

 

 

 

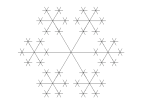
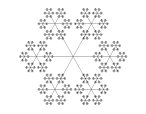
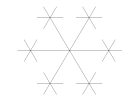
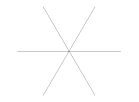
      а)            б)          в)                                      г)

Рис.1.12

    

1.6.  Об’єкти, що володіють фрактальними властивостями, в природі

У живій природі: корали, морські зірки і їжаки, морські раковини, квіти і рослини (броколі, капуста), плоди ( ананас), крони дерев і листя рослин, кровоносна система і бронхи людей і тварин.

У неживій природі: межі географічних об’єктів ( країн, областей, міст), берегові лінії, гірські хребти, сніжинки, хмари, блискавки, утворені на склі візерунки, кристали.

Фрактальними є дерева і папороті, що за своєю природою можуть моделюватись на комп’ютерах із використанням рекурсивних алгоритмів. Таку рекурсивність ясно видно на таких прикладах: гілка дерева або фронд від папороті є мініатюрним відтворенням цілого; не ідентичне, але схоже за природою.

Поверхня гір може моделюватись на комп’ютері з використанням фракталів: починати з трикутника в тривимірному просторі та з’єднати центральні точки кожного ребра відрізками, отримуючи 4 трикутники. Центральні точки потім зсуваються догори або донизу на випадкову відстань у фіксованому діапазоні. Процедура повторюється зі зменшенням діапазону на кожній ітерації вдвічі. Рекурсивна природа алгоритму гарантує , що ціле є статистично подібним до кожної із деталей.

Рис.1.13

При розриві двох вкритих клеєм листів акрилу утворюється фрактальний візерунок.

Рис.1.14

Високовольтний розряд в 4 блоці акрилу створює фрактальний рисунок Ліхтенберга.

Рис.1.15

Фрактальні тріщини з'являються на DVDдиску після обробки мікрохвильовим випроміненням.

Рис.1.16

Капуста «Romanesco broccoli» демонструє дуже дрібні природні фрактали.

Рис.1.17

Ö-фрактал.

У фізиці фрактали  природним чином  виникають при моделюванні нелінійних процесів, таких, як турбулентний плин рідини, складні процеси дифузії – адсорбції, полум’я, хмари тощо. Фрактали використовуються при моделюванні пористих матеріалів, наприклад, в нафтохімії. У біології вони застосовуються для моделювання популяцій і для опису систем внутрішніх органів (система кровоносних судин). Після створення кривої Коха було запропоновано використовувати її при обчисленні протяжності берегової лінії.

Фрактальну геометрію для проектування антенних пристроїв було вперше застосовано американським інженером  Натаном Коеном, який тоді жив у центрі Бостона, де було  заборонено встановлювати зовнішні антени на будинках. Натан вирізав з алюмінієвої фольги фігуру у формі кривої Коха та наклеїв її на аркуш паперу, а потім приєднав до приймача. Виявилось, що така антена працює не гірше за звичайну. Й хоча фізичні принципи роботи такої антени не вивчено досі, це помогло Коену заснувати власну компанію й налагодити їхній серійний випуск.

За допомогою фракталів можна стискати великі растрові зображення до частин їхніх нормальних розмірів. Це твердження випливає з теореми Банаха про стискуючі перетворення й є результатом роботи дослідника Технологічного інституту шт. Джорджія Майкла Барнслі.

Наприклад, закодувавши якесь зображення двома афінними перетвореннями, ми однозначно визначаємо його за допомогою 12 коефіцієнтів. Якщо тепер задати яку-небудь початкову точку (наприклад, X = 0, Y = 0) та запустити ітераційний процес, то ми після першої ітерації отримаємо дві точки, після другої — чотири, після третьої — вісім і т. д. Через кілька десятків ітерацій сукупність отриманих точок описуватиме закодоване зображення. Але проблема полягає в тому, що дуже важко знайти коефіцієнти перетворень, які кодували б довільне зображення.

Незважаючи на те, що було створено програмне забезпечення, що реалізує ці алгоритми (наприклад, бібліотеки фрактального стиснення використовуються в Microsoft Encarta), досить ефективного методу не було знайдено досі, а сам Майкл Барнслі продовжує працювати в даному напрямкові.

 

 

Висновок розділу:

Отже, фракта́л (лат. fractus — подрібнений, дробовий) – нерегулярна, самоподібна структура, це малюнок, що складається з подібних (ідентичних) між собою елементів. Розвитком науки фракталів займалось багато вчених, перший хто дав назву «фрактал» таким фігурам - Бенуа Мандельброт. Фрактали можна створювати 3 способами. Вони мають різні види самоподібності: точна самоподібність, майже самоподібність і статистична самоподібність. Алгебраїчні, геометричні, стохастичні - види фракталів. Вони поширені в живій і неживій природі. 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

РОЗДІЛ 2.

 ЗНАХОДЖЕННЯ ФРАКТАЛЬНОЇ СТРУКТУРИ У ТРИКУТНИКУ ПАСКАЛЯ, ФІГУРНИХ ЧИСЛАХ, ЛІТЕРАТУРНИХ ТВОРАХ

        2.1. Трикутник Паскаля

 

Облаштування трикутника Паскаля (рис.2.2) - бічні сторони одиниці, кожне число дорівнює сумі двох розташованих над ним. Трикутник можна продовжувати необмежено.Трикутник Паскаля  служить для обчислення коефіцієнтів розкладання виразів виду(x+1) ⁿ.  Розпочавши з трикутника з одиниць, обчислюють значення на кожному послідовному рівні шляхом складання сусідніх чисел; останньою ставлять одиницю. Таким чином, можна визначити, наприклад, що (x + 1) ⁴ = 1x⁴ + 4x³ + 6x² + 4x + 1x⁰. При виділенні непарних чисел в трикутнику Паскаля  виходить трикутник Серпінського (рис.2.1). Візерунок демонструє властивість коефіцієнтів, вживану при «арифметизації» комп'ютерних програм, яка перетворить їх в рівняння алгебри.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

                          

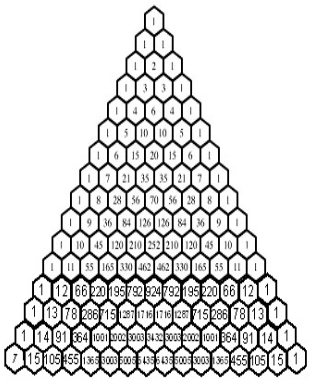
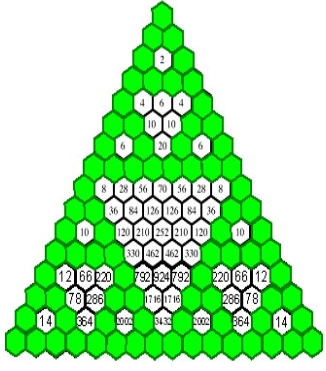
                   Рис.2.1                                                               Рис.2.2

 

 

         2.2. Фігурні числа

        Фігурні числа (рис.2.3) — це за­гальна назва чисел, пов'я­заних з тією чи іншою гео­метричною фігурою.

 

 

 

 

 

 

 

 

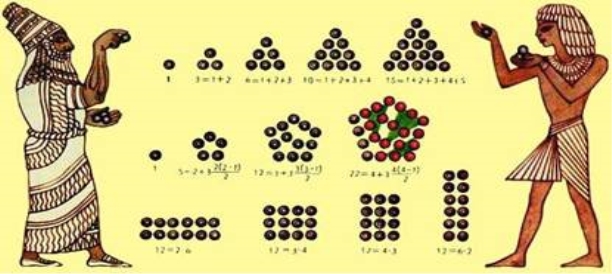
Рис.2.3

Піфагор уперше, в VI ст. до нашої ери, звернув увагу на те, що, допомагаючи собі при рахунку камінчиками, люди іноді вибудовують камені в правильні фігури. Можна просто класти камінчики в ряд: один, два, три. Якщо класти їх в два ряди, щоб виходили прямокутники, ми виявимо, що виходять усі парні числа. Можна викладати камені в три ряди: вийдуть числа, що діляться на три. Всяке число, яке на що-небудь ділиться, можна представити прямокутником, і тільки прості числа не можуть бути «прямокутниками».

•        ЛІНІЙНІ ЧИСЛА — числа, що не розкладаються на співмножники, тобто їх ряд співпадає з рядом простих чисел, доповненим одиницею:

1,2,3,5,7,11,13,17,19,23,.... Це прості числа.

(лінійне число 5)

•        ПЛОСКІ ЧИСЛА — числа, представимо у вигляді добутку двох співмножників, тобто складові: 4, 6, 8, 9, 10, 12, 14, 15,...

(плоске число 6)

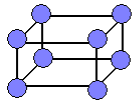•        ТІЛЕСНІ ЧИСЛА — числа, представимо добутком трьох співмножників: 8, 12, 18, 20, 24, 27, 28,... і т. д.

(тілесне число 8)

 

 

МНОГОКУТНІ ЧИСЛА:

• ТРИКУТНІ ЧИСЛА: 1, 3, 6, 10, 15, 21, 28, 36, 45, 55, ...

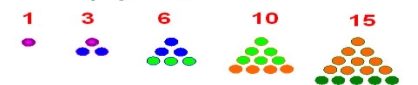
Перше число - 1. Наступне число - 3. Воно виходить збільшенням до попереднього числа, 1, двох точок, щоб шукана фігура стала трикутником. На третьому кроці ми додаємо три точки, зберігаючи фігуру трикутник. На подальших кроках додається n точок, де n - порядковий номер трикутного числа. Кожне число виходить додаванням до попереднього певної кількості точок. З цієї властивості вийшла рекурентна формула для трикутних чисел:  t n=n+t _{n - 1}.

• КВАДРАТНІ ЧИСЛА є добутком двох однакових чисел, тобто є повними квадратами: 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, ..., n2, ...

Перше число - 1. Наступне число - 4. Воно виходить збільшенням 3 точок до попереднього числа у вигляді прямого кута, щоб вийшов квадрат. Формула для квадратних чисел дуже проста, вона виходить з назви цієї групи чисел : gn = n². Але також, окрім цієї формули, можна вивести рекурентну формулу для квадратних чисел.

 

 

g1 = 1

g2 = 4 = 1+3 = 1+2 ∙2-1

g3 = 9 = 4+5 = 4+2∙ 3-1

g4 = 16 = 9+7 = 9+2∙ 4-1

g5 = 25 = 16+9 = 16+2∙ 5-1

• П’ЯТИКУТНІ ЧИСЛА: 1, 5, 12, 22, 35, 51, 70, 92, 117, 145, ...

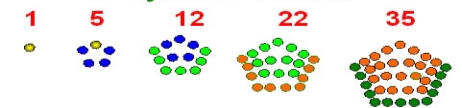
Перше число - 1. Наступне число - 5. Воно виходить збільшенням чотирьох точок, таким чином, фігура, що вийшла, набуває форми п'ятикутника. Одна сторона такого п'ятикутника містить 2 точки. На наступному кроці на одній стороні буде 3 точки, загальна кількість точок - 12. Спробуємо вивести формулу для обчислення п'ятикутних чисел. Перші п'ять п'ятикутних чисел: 1, 5, 12, 22, 35. Вони утворюються таким чином:

f1 = 1

f2 = 5 = 1+4 = 1+3∙ 2-2

f3 = 12 = 5+7 = 5+3∙ 3-2

f4 = 22 = 12+10 = 12+3∙ 4-2

f5 = 35 = 22+13 = 22+3∙ 5-2 

• ШЕСТИКУТНІ ЧИСЛА (1, 6, 15, 28, 45, ...)

 

 

 

 

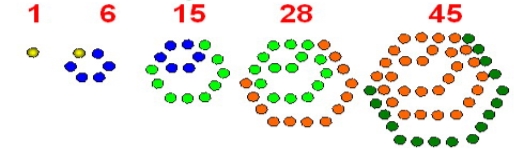
 Перше число - 1. Друге - 6. Фігура виглядає як шестикутник із стороною в 2 точки. На третьому кроці вже 15 точок вибудовуються у вигляді шестикутника із стороною 3 точки. Виведемо рекурентну формулу:

u1 = 1

u2 = 6=1+4∙ 2-3

u3 = 15 = 6+4∙ 3-3

u4 = 28 = 15+4∙ 4-3

u5 = 45 = 28+4∙5-3

Якщо подивитися уважніше, то можна помітити зв'язок між усіма рекурентними формулами.

Для трикутних чисел: tn=t _{n - 1}+n= t _{n - 1}+1n-0

Для квадратних чисел: gn = g _{n - 1}+2n-1

Для п'ятикутних чисел: fn = f _{n - 1}+3n-2

Для шестикутних чисел: un = u _{n - 1}+4n-3

ДЕЯКІ  ВЛАСТИВОСТІ  ФІГУРНИХ ЧИСЕЛ

1.Сума двох  послідовних трикутних  чисел є повним   квадратом

2.Парність   елементів ряду  трикутних чисел  змінюється за законом: непарне, непарне, парне, парне…

3.Зв'язок між  трикутними   та квадратними  числами:

8Т_n + 1 =К_2n+1 (формула Діофанта). 

2.3. Літературні твори.

Розглянемо фрактал саме як витвір мистецтва, що характеризується двома основними характеристиками:

1) частина його деяким чином подібна до цілого(в ідеалі, ця послідовність подібностей поширюється на нескінченність, хоча ніхто ніколи не бачив дійсно нескінченної послідовності ітерацій, що будують сніжинку Коха;

2) його сприйняття відбувається по послідовності вкладених рівнів. Помітимо, що чарівність фрактала якраз і виникає на шляху дотримання по цій заворожливій і запаморочливій системі рівнів, повернення з якої не гарантоване.

Як же можна створити нескінченний текст? Це питання ставив герой розповіді Х.Л.Борхеса «Сад стежинок», що розходяться: «Я задавався питанням, як може книга бути нескінченною. У голову не приходить нічого, окрім циклічного тому, тому, в якому остання сторінка повторює першу, що йде по кругу, що і дозволяє йому тривати скільки завгодно».

Подивимося, які ще рішення можуть існувати. Найпростішим нескінченним текстом буде текст з нескінченної кількості елементів, що дублюються, або куплетів, частиною якого, що повторюється, є його «хвіст» - той же текст з будь-якою кількістю відкинутих початкових куплетів. Схематично такий текст можна зображувати у вигляді дерева, що не розгалужується, або періодичної послідовності куплетів, що повторюються. Одиниця тексту - фраза, строфа або розповідь, починається, розвивається і закінчується, повертаючись у вихідну точку, точку переходу до наступної одиниці тексту, що повторює початкову. Такий текст можна уподібнити нескінченному періодичному дробу: 0,33333., її ще можна записати як 0,(3). Видно, що відсікання «голови» - будь-якої кількості початкових одиниць, нічого не змінить, і «хвіст» в точності співпадатиме з цілим текстом.

Серед таких нескінченних творів - вірші для дітей або народні пісеньки.

На відміну від нескінченних куплетів, фрагменти фракталів Мандельброта все ж не тотожні, а подібні один до одного, і ця якість і надає їм чарівність. Тому у вивченні літературних фракталів встає завдання пошуку подібності, схожості (а не тотожності) елементів тексту.

У разі нескінченних куплетів заміна тотожності на подібність була здійснена різними способами. Можна привести, принаймні, дві можливості:

1. створення віршів з варіаціями; 
2. тексти з нарощуваннями.

Вірші з варіаціями - це, наприклад, українська народна пісня (додаток А)

Ще одна можливість криється в текстах з « приростами». Такі відомі нам з дитинства казки про ріпку або про колобка, в кожному епізоді яких кількість персонажів збільшується.

Такі тексти мають структуру «ялиночки» у яких кожен рівень   повторює попередній зі збільшенням розміру зображення. В українській літературі аналогом є казка «Рукавичка».  

Висновок розділу

Отже, фрактали тісно пов’язані із трикутником Паскаля – якщо виділити в ньому непарні числа , то отримаємо трикутник Серпінського, фігурними числами -ми бачимо, що фігурні числа побудовані на повторюваності: це добре видно на рекурентних формулах, можна сміливо стверджувати, що фігурні числа у своїй основі мають фрактальну структуру і літературними творами – це створення віршів із варіаціями і текстів із нарощуванням.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ВИСНОВКИ

 

        У моїй роботі ви прочитали цікаву інформацію про фрактали, їх види, розмірність і властивості, про їх застосування, а також про трикутник Паскаля, фігурні числа, про фрактальні літературні твори і багато що інше. Отже, фракта́л (лат. fractus — подрібнений, дробовий) – нерегулярна, самоподібна структура, це малюнок, що складається з подібних (ідентичних) між собою елементів. Розвитком науки фрак-талів займалось багато вчених, перший хто дав назву «фрактал» таким фігурам - Бенуа Мандельброт. Фрактали можна створювати 3 способами. Вони мають різні види самоподібності: точна самоподібність, майже самоподібність і статистична самоподібність. Алгебраїчні, геометричні, стохастичні - види фракталів.          Вони поширені і в живій і неживій природі. Фрактали тісно пов’язані із трикутни-ком Паскаля – якщо виділити в ньому непарні числа , то отримаємо трикутник Серпінського, фігурними числами ми бачимо, що фігурні числа побудовані на пов-торюваності: це добре видно на рекурентних формулах, можна сміливо стверджу-вати, що фігурні числа у своїй основі мають фрактальну структуру і літературними творами – це створення віршів із варіаціями і текстів із нарощуванням.

              В процесі дослідження була виконана наступна робота:

Проаналізована і опрацьована  література по темі дослідження.

Розглянуті і вивчені різні  види фракталів.

Зібрана колекція фрактальних образів для первинного ознайомлення зі світом фракталів.

 Знайдені об’єкти, що володіють фрактальними властивостями, в природі.

Встановлені взаємозв'язки між фракталами і трикутником Паскаля, літературними творами, фігурними числами.

              Я переконався, що тим, хто займається фракталами, відкривається прекрас-ний, дивовижний світ, в якому панують математика, природа і мистецтво. Я думаю, що після знайомства з моєю роботою, ви, як і я, переконаєтеся в тому, що математика прекрасна і дивовижна.

 

СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ

 

1.                   Божокин С.В., Паршин Д.А. Фрактали і мультифрактали. Іжевськ: НИЦЬ «Регулярна і хаотична динаміка», 2001. - 128с.
2.                   Волошинов А. В. Математика і мистецтво : Кн. для тих, хто не лише любить математику і мистецтво, але і бажає замислитися про природу прекрасного і красу науки. 2-е видавництво, доро0б. і доп. - М.: Просвіта, 2000. - 399с.
3.                   Гарднер М. А. Ненудна математика. Калейдоскоп головоломок .  М.: АСТ: Астрель, 2008. - 288с.: мул.
4.                   Гринченко В. Т., Маципура В.Т., Снарський А.А. Введення в нелінійну динаміку. Хаос і фрактал. Видавництво: ЛКИ, 2007 р. 264 стор.
5.                   Мандельброт Б. Фрактальна геометрія природи. — М.: «Інститут комп'ютерних досліджень», 2002.

« ІНТЕРНЕТ - РЕСУРСИ»:

6. http://uk.wikipedia.org/wiki

7. http://www.fractals.narod.ru/tips.htm

8. http://algolist.manual.ru/graphics/fracart.php

  9. http://sakva.narod.ru/fractals.htm

ДОДАТКИ

 

Додаток А. Українська народна пісня  « Як служив же я у пана»  з варіаціями.

 

Як служив же я у пана
Тай на перше літо та літо
Заробив же я у пана
Курочку за літо.

А та курка-чубатурка
Нема пір’їв сама шкурка
По садочку ходить та й ходить,
Курчаточок водить та й водить.

Як служив же я у пана
Тай на друге літо та літо
Заробив же я у пана
Качечку за літо.

А та качка ках ках ках ках
А та курка-чубатурка...
Нема пір’їв сама шкурка
По садочку ходить та й ходить,
Курчаточок водить та й водить

Як служив же я у пана
Тай на третє літо та літо
Заробив же я у пана
Гусочку за літо.

А те гуся суся-сюся,
А та качка ках ках ках ках
А та курка-чубатурка...
Нема пір’їв сама шкурка
По садочку ходить та й ходить,
Курчаточок водить та й водить

Як служив же я у пана
Та й четвертеє літо та літо
Заробив же я у пана
Індика за літо.

А той індик дик-дик, дик-дик,
А те гуся суся-сюся,
А та качка ках ках ках ках
А та курка-чубатурка...
Нема пір’їв сама шкурка
По садочку ходить та й ходить,
Курчаточок водить та й водит

Як служив же я у пана
Тай на п’яте літо та літо
Заробив же я у пана
Телятко за літо

А те теля хвостиком виля
А те гуся суся-сюся,
А та качка ках ках ках ках
А та курка-чубатурка...
Нема пірев сама шкурка
По садочку ходить та й ходить,
Курчаточок водить та й водит

Як служив же я у пана
Тай на шосте літо та літо
Заробив же я у пана
Дівчину за літо

А те дівча напилося
З печі впала тай вбилося
А те теля хвостиком виля
А те гуся суся-сюся,
А та качка ках ках ках ках
А та курка-чубатурка...
Нема пір’їв сама шкурка
По садочку ходить та й ходить,
Курчаточок водить та й водить