Контрольна робота "Розв'язування трикутників"

ВАРІАНТ 1

1. (0,5 бала) Квадрат будь-якої сторони трикутника дорівнює:

а) сумі квадратів двох інших сторін;   

б)  сумі квадратів двох інших сторін трикутника без подвоєного добутку цих сторін на косинус кута між ними; 

в)  сумі квадратів двох інших сторін трикутника без подвоєного добутку цих сторін на синус кута між ними;   

г) подвоєному добутку інших сторін

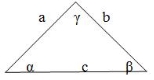
2. (0,5 бала) Вибрати вірне твердження: 

 а) ;    б) ;    в) ;  

 г)

3. (0,5 бала) cos(90°-α)=

а)  sinα;    б)  -sinα;    в)  cosα;    г)-cosα

4. (0,5 бала) cos150°=

а) ;    б) ;    в) ;    г)

5. (0,5 бала) Спростити вираз 2(sinα+ cosα) +3.

а) 1  ;    б) -2  ;    в) 5 ;    г) 4

6. ( 0,5 бала) Сторони трикутника МКР дорівнюють m,k,p. Яким буде кут, протилежний стороні m, якщо m> k+p?

а) гострим  ;    б) тупим ;    в)  прямим;    г) неможливо визначити

7.(1 бал) Знайти радіус кола, описаного навколо трикутника АВС, якщо АВ=5 см, ∠С=30.

а) см ;    б) 5 см ;    в) 10 см ;    г) см

8. (1 бал) Дві сторони трикутника 6 см і 4 см, кут між ними -120°. Знайти довжину третьої сторони трикутника.

а) см;    б)  см;    в) см ;    г) см

9. (1 бал) Два кути трикутника дорівнюють 60° і 45°, сторона, що лежить проти меншого з цих кутів дорівнює см. Знайти довжину сторони трикутника, яка лежить проти більшого з цих кутів.

а) 8 см ;    б) см ;    в) см ;    г) см

10. (2 бали) Знайти невідомі сторони і кути трикутника АВС, якщо АВ=16см, ∠ А=38°,∠ В=49°.

11. (2 бали) В паралелограмі АВСD сторона ВС=а, ∠ВАС=α, ∠САD=β. Знайти діагональ АС паралелограма.

12. (2 бали) Сторони трикутника 13см,14см і 15см. Знайти висоту трикутника, опущену на сторону, довжина якої 15 см.
 

ВАРІАНТ 2

1. (0,5 бала) Квадрат будь-якої сторони трикутника дорівнює:

а) сумі квадратів двох інших сторін;   

б)  сумі квадратів двох інших сторін трикутника без подвоєного добутку цих сторін на косинус кута між ними; 

в)  сумі квадратів двох інших сторін трикутника без подвоєного добутку цих сторін на синус кута між ними;  

 г) подвоєному добутку інших сторін

2. (0,5 бала) Вибрати вірне твердження: 

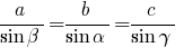 а) ;    б) ;    в) ;

   г)

3. (0,5 бала) sin(90°-α)=

а)  sinα;    б)  -sinα;    в)  cosα;    г)-cosα

4. (0,5 бала) cos120°=

а) ;    б) ;    в) ;    г)

5. (0,5 бала) Спростити вираз 2(sinα+ cosα) - 4.

а) 1  ;    б) -2  ;    в) 5 ;    г) 4

6. (0,5 бала) Сторони трикутника МКР дорівнюють m,k,p. Яким буде кут, протилежний стороні m, якщо m< k+p?

а) гострим  ;    б) тупим ;    в)  прямим;    г) неможливо визначити

7. (1 бал) Знайти радіус кола, описаного навколо трикутника АВС, якщо АВ=10 см, ∠С=30.

а) см ;    б) 5 см ;    в) 10 см ;    г) см

8. (1 бал) Дві сторони трикутника 5 см і 3 см, кут між ними -120°. Знайти довжину третьої сторони трикутника.

а) см;    б)  7 см;    в) см ;    г) см

9. (1 бал) Два кути трикутника дорівнюють 60° і 45°, сторона, що лежить проти більшого з цих кутів дорівнює см. Знайти довжину сторони трикутника, яка лежить проти меншого з цих кутів.

а) 8 см ;    б) см ;    в) см ;    г) см

 10. (2 бали) Знайти невідомі сторони і кути трикутника АВС, якщо ВС=4см, ∠ C=115°,∠ В=48°.

11. (2 бали) В паралелограмі АВСD сторона ВС=b, ∠ВАС=, ∠САD=. Знайти діагональ АС паралелограма.

12. (2 бали) Сторони трикутника 13см,14см і 15см. Знайти висоту трикутника, опущену на сторону, довжина якої 14 см.