Підготовка до ЗНО.Первісна.Інтеграл.

Підготовка до НМТ

1. Первісна . Таблиця первісних.2. Невизначений інтеграл.3. Визначений інтеграл. Формула. Ньютона-Лейбніца 4. Знаходження площ криволінійних трапецій за допомогою визначеного інтеграла.

Поняття первісноїДія знаходження первісної функції називається інтегруванням. Вона обернена до дії диференціювання. Функція F(x) на деякому проміжку є первісною для f(x), якщо для всіх х із цього проміжку виконується рівність:𝑭′𝒙=𝒇𝒙 

Приклади

хy , Основна властивість первісної(Будь-які дві первісні однієї і тієї самої функції відрізняються одна від одної на сталий доданок)

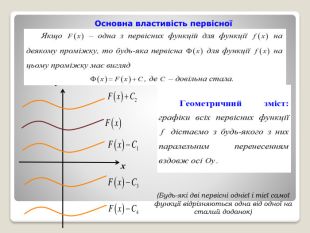
Правила знаходження первісної Нагадаємо, що операція знаходження похідної для заданої функції називається диференціюванням. Обернена операція знаходження первісних для даної функції називається інтегруванням. Правила інтегрування можна також одержати за допомогою правил диференціювання. Правило 1. Якщо F(x) і G(x) — первісні відповідно функцій f(x) і g(x) на деякому проміжку, то функція F(x) ± G(x) є первісною функції f(x) ± g(x). Правило 2. Якщо F(x) є первісною для функції f(x), a C — стала, то CF(x) — первісна для функції Cf(x). Правило 3. Якщо F(x) є первісною для f(x), a k і b — постійні числа, причому k 0, то F(kx +b) є первісною для функції f(kx + b).

Таблиця первісних (невизначених інтегралів)

Спробуйте самостійно. НМТ

Знаходження первісних, що задовольняють задані початкові умови. Знайдемо первісну функції 𝑓𝑥=1+𝑥2, графік якої проходить через точку 𝑀−1;2 :  𝐹𝑥=𝑥+𝑥33+ 𝐶 𝐹−1=−1+−133+𝐶=2; −43+𝐶=2; С= 313. 𝐹𝑥=𝑥+𝑥33+ 𝐶 313.     

Спробуйте самостійно. НМТ

Поняття інтеграла. Сукупність усіх первісних однієї і тієї ж функції називається невизначеним інтегралом і позначається: хy знак інтеграла, підінтегральна функція, знак диференціала (похідної), первісна, стала.

Правила інтегрування

Таблиця первісних (невизначених інтегралів)

Приклади знаходження невизначених інтегралів

Приклади знаходження невизначених інтегралів. Приклад 4. Приклад 5. Приклад 6.

Криволінійна трапеція

Площа криволінійної трапеції

Визначений інтеграл

Властивості визначених інтегралів

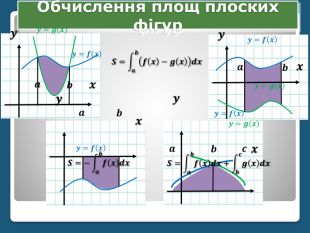
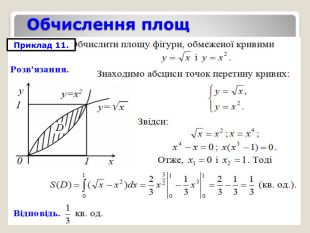
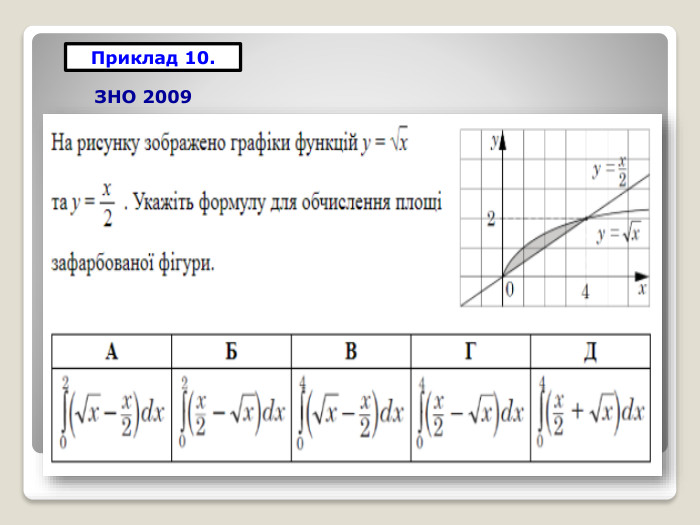
Алгоритм знаходження площі криволінійної трапеціїПобудувати геометричну фігуру, обмежену заданими лініями. Перевірити, чи є фігура криволінійною трапецією. Знайти первісну функції, яка обмежує криволінійну трапецію зверху. Виділити межі інтегрування (відрізок на який фігура «спирається»). Підставити необхідні дані в формулу та обчислити площу криволінійної трапеції.𝒙 𝒚 𝒂 𝒃 𝒚=𝒇𝒙 𝑆=𝑎𝑏𝑓(𝑥)𝑑𝑥=𝐹(𝑏)−𝐹(𝑎) 

Обчислення площ плоских фігур𝒙 𝒚 𝒙 𝒚 𝑺=𝒂𝒃𝒇𝒙−𝒈𝒙𝒅𝒙 𝒂 𝒃 𝒚=𝒇𝒙 𝒚=𝒈𝒙 𝒚=𝒇𝒙 𝒚=𝒈𝒙 𝒙 𝒚 𝒂 𝒃 𝒚=𝒇𝒙 𝒙 𝒚 𝒂 𝒃 𝒚=𝒇𝒙 𝒚=𝒈𝒙 𝒂 𝒃 𝒄 𝑺=−𝒂𝒃𝒇𝒙𝒅𝒙 𝑺=𝒂𝒃𝒇𝒙𝒅𝒙+𝒃𝒄𝒈𝒙𝒅𝒙 

Обчислення визначених інтегралів

Обчислення визначених інтегралів

Обчислення визначених інтегралів

Обчислення площ. Приклад 8. Д

ЗНО 2019 Приклад 9.

Приклад 10. ЗНО 2009

Обчислення площ. Приклад 11.

Обчислення площ. Приклад 12.

Обчислення площ. Приклад 13.

Спробуйте самостійно. НМТ

НМТСпробуйте самостійно

Бажаю успіхів на шляху до вивчення математики!