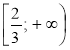Функції. Властивості функції: нулі функції, проміжки знакосталості, зростання і спадання функції.
Тема уроку. Функції. Властивості функції: нулі функції, проміжки знакосталості, зростання і спадання функції.
Мета уроку: повторити й систематизувати набуті учнями у 7 та 8 класах знання про означення, властивості числових функцій та приклади елементарних числових функцій і вигляд їхніх графіків. Сформувати знання учнів про спосіб задання функції формулою у = f(x). Повторити та систематизувати вміння учнів знаходити значення функції, що відповідає даному значенню аргументу, за даною формулою, і навпаки, а також уміння розв'язувати задачі на знаходження області визначення, області значень функції, а також умінь працювати з готовим графіком функції; виробити оперативні вміння роботи з формулою y = f(x).
Тип уроку: систематизація знань та вмінь, формування знань, вироблення вмінь.
Наочність та обладнання: опорний конспект № 12.
Хід уроку
I. Організаційний етап
Учитель повідомляє учням про зміст, орієнтовний план вивчення теми 2 та графік проведення контрольних робіт.
II. Перевірка домашнього завдання
Оскільки домашнє завдання попереднього уроку полягало у самостійному виконанні аналізу контрольної роботи за розданими вчителем розв'язаннями, на цьому етапі уроку достатньо провести роботу з роз'яснення найскладніших для учнів моментів контрольної роботи. У разі необхідності вчитель може роздати учням індивідуальні завдання на відпрацювання проблемних моментів.
ІІІ. Формулювання мети і завдань уроку.
Мотивація навчальної діяльності учнів
Учитель нагадує учням про те, що однією з основних змістовних ліній курсу алгебри середньої школи є функціональна лінія. Також учитель нагадує учням, що деякі відомості про функції (означення функції, означення області визначення функції, області значень функції, графіка функції тощо) учні вже отримали в 7 та 8 класах. Проте вивчених відомостей недостатньо для того, щоб розв'язувати деякі практичні задачі (порівняння значень функцій без обчислення цих значень і т. д.). Тому на цьому уроці постає питання про повторення основних означень та властивостей функцій, а також про існування деяких інших властивостей функцій, вивчення цих властивостей і формування певних оперативних умінь застосовувати ці властивості для розв'язування задач. Останнє твердження виражає головну дидактичну мету даного та наступного уроків.
IV. Актуалізація опорних знань та вмінь учнів
Усні вправи
- Виконайте дії:
1) -1,73 – 2,77; 2) -4,5 ∙ 0,4; 3) 43 : 23;
4) -0,6 ∙ (-0,3) - 0,2; 5) (3,1 + 0,09)0 : ![]() ; 6) (-7 + 2,5) : 1,5.
; 6) (-7 + 2,5) : 1,5.
- Знайдіть значення виразу:
1) 3 – 2а при а = -3; 2) 2х - 5 при х = 3;
3) ![]() х +
х + ![]() у при x = 24, y = -16.
у при x = 24, y = -16.
-
При яких значеннях змінної існує вираз:
1) х + 9; 2)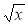 + 9; 3)
+ 9; 3) 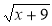 ; 4)
; 4) 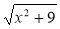 ;
;
5)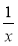 + 9; 6)
+ 9; 6) 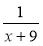 ; 7)
; 7) 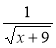 ?
?
V. Систематизація та доповнення знань
План вивчення матеріалу
- Означення числової функції. Супутні поняття. Задання функції формулою y = f(x).
- Область визначення функції. Як знайти область визначення функції, заданої формулою y = f(x).
- Область значень функції.
- Графік функції.
- Основні види елементарних функцій, вивчені у 7 та 8 класах, їхні властивості та графіки.
Опорний конспект № 12
|
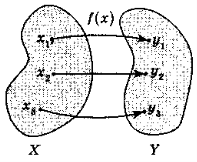
Функція — це залежність змінної у від змінної х, при якій кожному значенню х відповідає єдине значення у. |
|||||
|
|
Позначається: y = f(x), де х — аргумент (незалежна змінна); у — функція, значення функції (залежна змінна); f(x0) — значення функції в точці х0. |
||||
|
Приклад. Дано функцію f(x) = x2 - 3х + 2. Знайдемо: 1) f (0) 2) f (-1); 3) f (а). Розв’язання |
|||||
|
1) f (0) = 02 – 3 ∙ 0 + 2 = 2; 2) f (-1) = (-1)2 – 3 ∙ (-1) + 2 = 6; 3) f (a) = a2 – 3a + 2. |
|||||
|
|
Область визначення функції D(f) — це множина всіх значень, яких набуває аргумент. |
|
|||
|
|
Як знайти область визначення функції y = f(x) |
|
|||
|
|
1. Якщо f(x) — многочлен, то D(f) = R. |
|
|||
|
2. Якщо |
|||||
|
3. Якщо |
|||||
|
Приклад. Знайдемо область визначення функції: |
|||||
|
|
Розв'язання |
|
|||
|
|
1) 3х2 – х + 1 — многочлен, тому D(y) = R;
2)
3)
Отже, D(y) = (-∞; 0) |
|
|||
|
|
Область значень функції E(f) — множина всіх значень змінної у, яких вона може набувати при всіх значеннях аргументу, взятих з D(f). |
|
|||
|
|
Приклад. Знайдемо область значень функції у = Розв'язання |
|
|||
|
|
При всіх x |
|
|||
|
|
Числовою функцією називають функцію, область визначення й область значень якої є числовими множинами. |
|
|||
|
|
Графіком функції y = f(x) називають множину всіх точок координатної площини з координатами (х; f(x)), де х «пробігає» всю область визначення f(x) (a y — відповідне значення функції / у точці х). |
|
|||
|
|
Деякі елементарні функції та їхні графіки |
|
|||
|
|
1. y = kx + b —лінійна функція
|
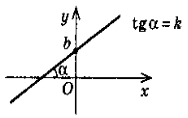
2. у = x2
|
|
||
|
|
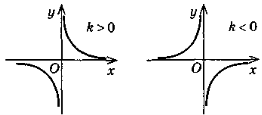
3. у =
|
4. y =
|
|
||
|
|
|
|
|
||
Методичний коментар
Навчальний матеріал уроку складається в основному з матеріалу, який було засвоєно учнями в 7 та 8 класах (новим є лише спосіб задання функції формулою y = f(x)). Проте обсяг навчального матеріалу досить великий. Тому для більш раціонального використання навчального часу на уроці вчитель може організувати роботу учнів з повторення та систематизації матеріалу як самостійну роботу з текстом підручника або з текстом, що міститься в опорному конспекті № 12. Докладними поясненнями вчителя можуть бути доповнені питання про спосіб задання функції формулою y = f(x) і способи роботи з нею та про відшукання області визначення функції, заданої формулою y = f(x).
VI. Формування вмінь
Усні вправи
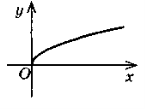
Функція задана формулою f (x) = ![]() .
.
1) Що означають записи f (2) і f (-8)?
2) Чому дорівнюють значення виразів f (2) і f (-8) ?
3) Яка область визначення функції?
4) Який із даних графіків є графіком цієї функції?
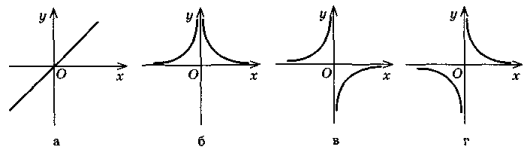
Письмові вправи
Вправи, запропоновані для розв'язування на даному уроці, мають відтворювати стандартні ситуації, розглянуті вище:
- для функції, заданої формулою у = f(x), знайти значення функції для заданого значення аргументу, і навпаки;
- для функції, заданої формулою у = f(x), знайти область визначення;
- за даним графіком функції знайти значення функції для заданого значення аргументу, знайти значення аргументу для заданого значення функції, знайти область визначення та область значень;
- для функції, заданої формулою у = f{x), визначити, які з точок лежать на графіку, а які не належать йому, а також визначити точки перетину графіка з координатними осями.
VII. Підсумки уроку
Контрольні запитання
- Через яку з даних точок проходить графік функції у = х2 + 2 ?
1) А(-2; 0); 2) В(-2; -2); 3) С(-2; 6); 4) D(-2; 2).
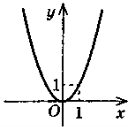
- Областю визначення якої з наведених функцій є проміжок (9; + ∞)?
1) y = ![]() ; 2) у =
; 2) у = ![]() ; 3) у =
; 3) у = ![]() ; 4) у =
; 4) у = ![]() .
.
VIII. Домашнє завдання
- Вивчити зміст нових понять (див. опорний конспект № 12).
- Розв'язати вправи, аналогічні за змістом розглянутим на уроці.
- Повторити розв'язування лінійних нерівностей з однією змінною.

про публікацію авторської розробки
Додати розробку