Лінійна функція, її графік та властивості.
Тема. Лінійна функція, її графік та властивості.
Мета: ознайомити учнів із «особливими випадками» лінійної функції і її графіком; узагальнити уяву учнів про зв'язок між k та b і графіком; подальше вдосконалювати вміння будувати й читати графіки лінійних функцій.
Тип уроку: засвоєння вмінь та навичок.
Хід уроку
I. Організаційний момент
(див. попередній урок)
II. Перевірка домашнього завдання
Перевірку виконання домашнього завдання можна організувати як самопе-ревірку за зразком (№ 2) і (або) провести математичний диктант.
- Математичний диктант
Варіант 1 [2]
1) Функція – у = 3x + 2 [у = -2х – 3] називається...
2) Лінійну функцію задано рівнянням у = 2 – 7x [у = -7 + 2х]. Назвіть коефіцієнти k та b у рівнянні цієї функції.
3) Графік лінійної функції перетинає вісь Ох під гострим кутом, а вісь Оу в т. (0; 1) [вісь Ох під тупим кутом, а вісь Оу в т. (0; -7)]. Що ви можете сказати про коефіцієнти k та b?
Побудуйте графік функції у = 5 – х [у = х – 2].
(Після проведення математичного диктанту проводиться самоперевірка та корекція — робота в парах.)
- Випереджальне домашнє завдання (№ 3) перевіряємо під час фронтального обговорення (правильно побудовані графіки заздалегідь зображено на дошці або вчителем, або одним—двома учнями). Після перевірки обговорення доходимо висновку: положення графіків лінійних функцій відносно координатних осей та початку координат залежить від того, чи дорівнюють кутовий коефіцієнт та (або) коефіцієнт b нулю.
III. Формулювання мети й завдань уроку
Учитель разом з учнями, виходячи із результатів виконання математичного диктанту та висновків, здобутих під час перевірки випереджального домашнього завдання, формулює мсту: 1) з'ясувати, як у загальному випадку пов'язано значення кутового коефіцієнта й коефіцієнта в рівнянні лінійної функції із розташуванням графіка лінійної функції в системі координат; 2) подальша робота з вироблення вмінь працювати із графіком лінійної функції.
IV. Актуалізація опорних знань
Виконання усних вправ
-
Серед формул у = 12 – 10х; у = 4x – 0,5; у = 15х; у = х(1 – х); у = 1;
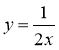 ;
; 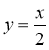 знайдіть ті, що задають лінійну функцію. Для даних формул укажіть k та b.
знайдіть ті, що задають лінійну функцію. Для даних формул укажіть k та b.
-
 Чи проходить графік функції у = -18x через точку
Чи проходить графік функції у = -18x через точку 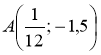 ; С (-0,1; -1,8)?
; С (-0,1; -1,8)?
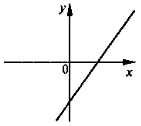
- Яка з функцій у = -3х + 2; у = -3х – 2; у = 3х – 2;
у = 3х + 2 може відповідати графіку, зображеному схематично. Чому?
V. Узагальнення знань
Виконання випереджального домашньої о завдання підводить учнів до висновку: якщо в рівнянні y = kx + b b = 0 (y = kx), то графік цієї лінійної функції проходить через початок координат; якщо в рівнянні у = kx + b k = 0 (у = b), то графік цієї лінійної функції проходить паралельно осі Ох. Висновки можна сформулювати у вигляді схем (учні записують у зошити).
|
Конспект 19 |
||
|
Залежність між розташуванням прямої у = kx + b та значеннями k і b |
||
|
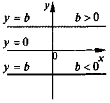
1) k = 0 у = b |
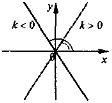
2) b= 0 y = kx |
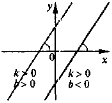
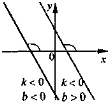
3) y = kx + b (k ≠ 0; b ≠ 0) |
|
|
|
|
Звернемо увагу учнів на той факт, що, якщо k = b = 0, графік лінійної функції збігається з віссю Ох (рівняння осі Ох: у = 0).
Але вісь Оу не є графіком жодної лінійної (і взагалі жодної) функції, бо для цього не виконується означення функції (одному значенню аргументу відповідає не одне, а безліч значень функції).
VI. Закріплення знань. Відпрацювання вмінь
Виконання усних вправ
- Опишіть, що являє собою графік функції, яку задано формулою:
1) у = 25х; 2) у = -70; 3) у = -0,01х; 4) у = 0.
- Знайдіть координати точки перетину з віссю Оу графіка лінійної функції:
1) у = 15х – 2; 2) у = -20х; 3) у = 16.
-
Графік лінійної функції — пряма, що паралельна осі Ох. Задайте цю
функцію формулою, якщо відомо, що її графік проходить через точку:
1) А(1; -4); 2) В(-5; 5); 3) C(0; 3,5).
Виконання письмових вправ
- Знайдіть точку перетину графіка функції у = -4х + 6 з осями координат.
-
Графік функції у = kх проходить через точку А(-8; 4). Знайдіть k. Чи проходить графік цієї функції через точку В (2; -1);
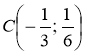 ?
?
- В одній системі координат побудуйте графік функції:
1) у = 4; 2) у = 1,5; 3) у = -2; 4) у = -х – 2; 5) у = х + 4; 6) у = 2х.
- Покажіть схематично, як розташований графік функції, заданої формулою:
1) у = 1,7х; 2) у = -3,1х + 2; 3) у = 2; 4) у = -2,3х;
5) у = kх + b, k > 0, b < 0; 6) у = kх + b, k < 0, b > 0.
- Логічна вправа.
|
у = х + 1 |
|
|
у = х – 1 |
? |
Який рисунок пропущено?
VII. Підсумки уроку
Охарактеризуйте коефіцієнти k та b у рівнянні лінійної функції, якщо графік цієї функції, зображений схематично, має вигляд:
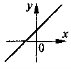
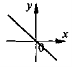
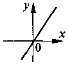
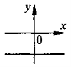
VIII. Домашнє завдання
№ 1. Чи перетинає вісь х графік лінійної функції і якщо перетинає, то в якій точці?
1) у = 100 – 25х; 2) у = 7х + 49; 3) у = 200х; 4) у = -75х; 5) у = -15; 6) у = 15.
№ 2. Удвох різних системах координат побудуйте графіки груп функцій:
1) у = 2; у = -2; у = 3; у = 7; 2) y = 1,5x; y = 1,5x – 3; y = 1,5x + 2.
Порівняйте кутові коефіцієнти графіків кожної групи та розташування графіків. Що ви помітили?


про публікацію авторської розробки
Додати розробку