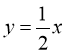Лінійна функція, її графік та властивості
Тема. Лінійна функція, її графік та властивості
Мета: ознайомити учнів із означенням лінійної функції та сформувати знання про графік та властивості лінійної функції; виробити первинні вміння будувати та читати графік лінійної функції.
Тип уроку: засвоєння нових знань.
Хід уроку
І. Організаційний момент
- Взаємоперевірка готовності учнів до уроку.
- Стан виконання домашнього завдання (звітують учні-консультанти).
Перевірка домашнього завдання
Завдання № 1 із виконаного домашнього є завданням на відтворення, тому перевірку можна виконати у вигляді взаємоперевірки за зразком.
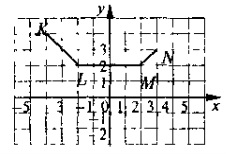
Зразок № 1
|
|
х |
-3 |
-3,5 |
-2 ≤ х ≤ 2 |
1,25 |
2,5 |
3,3 |
|
у |
3 |
3,5 |
2 |
2 |
2,5 |
3 |
|
|
Завдання № 2 є по суті випереджальним, бо готує учнів до сприйняття нового матеріалу (а може, й формує в учнів первинні
|
|||||||
уявлення про можливості класифікації функцій за видом формули, а також про зв'язок між видом формули, що задає функцію, та видом графіка).
Для перевірки цього завдання також можна презентувати зразки розв'язань (за якими учні в парах перевіряють роботи), а потім за цими готовими рисунками організувати роботу за алгоритмом порівняння.
|
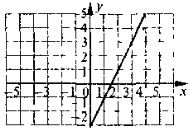
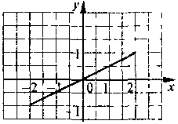
Зразок № 2 1) у = 2х – 3 |
|
|||||
|
х |
0 |
1 |
2 |
3 |
4 |
|
|
у |
-3 |
-1 |
1 |
3 |
5 |
|
|
|
||||||
|
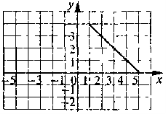
2) у = - х + 5
|
|
|||||
|
х |
1 |
2 |
3 |
4 |
5 |
|
|
у |
4 |
3 |
2 |
1 |
0 |
|
|
|
||||||
|
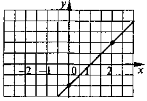
3) |
|
|||||||||
|
х |
-2 |
-1 |
0 |
1 |
2 |
|||||
|
у |
-1 |
-0,5 |
0 |
0,5 |
1 |
|||||
|
|
||||||||||
|
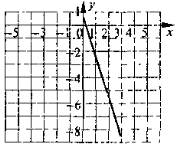
4) у = -3х + |
|
|||||||||
|
х |
0 |
1 |
2 |
3 |
||||||
|
у |
|
-2 |
-5 |
-8 |
||||||
|
|
||||||||||
Алгоритм порівняння
- За якими ознаками можна порівнювати ці функції та графіки?
- Як ви вважаєте, яка мета порівняння?
- Знайдіть спільне.
- Знайдіть подібне.
- Які висновки можна зробити?
III. Формулювання мети й завдань уроку
Після проведеної роботи з порівняння учні можуть зробити висновок щодо «схожості» (подібності всіх наведених функцій як за формулою так і за видом графіка); тоді метою уроку може бути знайомство з «узагальненою» формулою, яка представлена в домашньому завданні різними своїми видами, та з'ясування її основних властивостей.
IV. Актуалізація опорних знань
Ігровий момент «Найрозумніший»
- Відповідність між змінними у та х, за якої кожному значенню змінної х відповідає єдине значення змінної у — це... (Функція).
- Змінна х — ... (Аргумент).
- Змінна у — ... (Функція, значення функції).
- Усі значення, яких набуває аргумент, утворюють... (Область визначення функції).
- Усі значення, яких набуває функція при аргументах, взятих з області визначення функції, утворюють... (Область значень функції).
- Множина усіх точок координатної площини, абсциси яких дорівнюють значенню аргументу, а ординати — відповідним значенням функції, називається... (Графіком функції).
- Коефіцієнти многочлена 3х3 – 2х2 – х – 2 — це... (3; -2; -1; -2).
V. Вивчення нового матеріалу
З усіх питань, що підлягають вивченню з теми, на урок виносяться: означення лінійної функції та її графік (загального вигляду) та їх загальні властивості.
Викладання нового матеріалу можна провести за планом.
- Приклади величин, зв'язок між якими виражається функцією, вигляду у = kх + b.
- Означення лінійної функції.
- Властивості лінійної функції (область визначення та область значень).
- Графік лінійної функції загального вигляду (геометричний зміст). Зв'язок положення графіка лінійної функції із коефіцієнтами k та b. Записи, що їх виконують учні в зошитах, можуть мати вигляд:
|
Конспект 18 |
||||
|
Лінійна функція та її графік |
||||
|
1. Означення. Функція, яку можна задати формулюю у = kx + b, дe k i b числа, — лінійна функція. |
||||
|
Приклад: у = 2х + 2 (k = 3; b = 2) у = 2х – 3 (k = 2; b = -3) |
||||
|
у = - х + 5 (k= -1; b = 5) у = |
||||
|
2. Властивості лінійної функції |
||||
|
1) Область визначення — будь-яке число. 2) Область значень — будь-яке число. |
||||
|
3. Графік функції — пряма. Щоб побудувати графік, шукаємо координати будь-яких двох його точок. |
||||
|
Приклад. Побудувати графік функції у = х – 1 — лінійна, отже, графіком є пряма |
||||
|
|
х |
0 |
2 |
|
|
у |
-1 |
1 |
||
|
4. Властивості графіка лінійної функції |
||||
|
1) Якщо k > 0, то графік утворює з додатною піввіссю Ох гострий кут.
2) Якщо k < 0, то графік утворює з додатною піввіссю Ох тупий. |
||||
|
3) Число b показує ординату точки перетину графіка з віссю Оу |
||||
Оскільки повне уявлення учнів про числові множини та їх співвідношення ще не сформоване, то відповідь на питання про область визначення та область значень функції характеризуємо не зовсім «математично строгим поняттям» — будь-яке число.
VII. Первинне закріплення
На цьому уроці виробляємо вміння:
- розпізнавати лінійні функції та називати їх коефіцієнти;
- будувати графік лінійної функції та читати його;
- за формулою y = kx + b встановлювати властивості графіка.
Виконання усних вправ
- Які функції є лінійними? Для лінійних функцій назвати k і b.
1) у = х + 5; 2) у = -3х; 3) 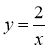 ; 4) у = 8; 5)
; 4) у = 8; 5) 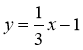 ; 6) у = 0;
; 6) у = 0;
7) у = 3 – 7x; 8) у = x2 + 4.
-
Під яким кутом перетинає вісь Ох графік функції:
1) у = -3х + 1; 2) у = 2х - 4?
В якій точці він перетинає вісь Оу?
Виконання письмових вправ
- Лілійну функцію задано формулою у = 2х – 6. Знайдіть: 1) значення функції, що відповідає значенню аргументу -6; 0; 9; 2) при якому значенні аргументу значення функції дорівнює -3; 0; 7?
Результати обчислень запишіть у таблицю:
|
х |
… |
|
у |
… |
-
Побудуйте графік функції за даною формулою:
1) у = х – 2; 2) у = -2х + 0,5; 3) у = 2х – 1.
Перевірте, чи відповідають ваті побудови властивостям графіка, які випливають із значень k та b.
- Чи проходить графік функції у = 1,8х + 9 через точку: А(10; 27),
В(50; 89), С(-20; -27)?
- Побудуйте графік функції у = -1,5х + 1. Користуючись графіком, знайдіть:
- значення у при х = -4; х = 0; х = 2;
- значення х, при якому у = -1; у = 4;
- усі значення х, при яких у > 1, у < 4;
- усі значення у, які відповідають значенням х >0.
VII. Підсумки уроку
- Учні називають нові поняття уроку.
- Яка з функцій «зайва»? Чому?
1) у = х – 1; 2) у = х + 1; 3) 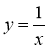 ; 4) у = -х.
; 4) у = -х.
VIII. Домашнє завдання
№ 1. Вивчіть означення і властивості нових понять уроку.
№ 2. Побудуйте графік функції, заданої формулою у = 0,5х – 3. Користуючись графіком, знайдіть:
- значення у, якому відповідає: х = -2; х = 2; х = 4;
- значення х, якому відповідає: у = -2; у = 1;
- усі значення х, при яких -3 ≤ у ≤ -1.
№ 3. Запишіть дані рівняння у вигляді y = kx + b та побудуйте графіки цих «нових» функцій. Порівняйте графіки й рівняння та зробіть висновки з порівнянь:
а) у = х, у = 3х; у = -3х; 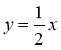 ; б) у = 3; у = 2; у = -3; у = 0,5.
; б) у = 3; у = 2; у = -3; у = 0,5.


про публікацію авторської розробки
Додати розробку