ЛІЦЕЙ

Новгородківської селищної ради Кропивницького району

Кіровоградської області

Вершино-Кам’янської філії

 

 

 

ФУНКЦІЯ

 у=ах2+вх+с, а≠0,

 ЇЇ ГРАФІК І ВЛАСТИВОСТІ

9 клас Алгебра

(Дистанційне навчання з використанням графічного планшету

HUION H610PRO V2)

 

 

 

 

 

                                                Вчитель математики

                                                                  Антоненко Валерій Вікторович

 

2022р.

9 клас Алгебра

Урок 34 (Дистанційне навчання з використанням графічного планшету HUION H610PRO V2)

Тема. ФУНКЦІЯ у=ах²+вх+с, а≠0, ЇЇ ГРАФІК І ВЛАСТИВОСТІ

Мета. Сформувати знання учнів про означення, вид графіка та алгоритм побудови графіка квадратичної функції.

Тип уроку. Урок засвоєння нових знань.

Хід уроку

1.    Організаційний момент.

1.     Перевірка наявності учнів у класі, в наявних на платформі  Meet.
2.     Перевірка готовності учнів до уроку.
3.     Запис у зошитах дати уроку і теми.

2.    Перевірка домашнього завдання.

Усно: (Учні дають відповіді на питання а вчитель записує за допомогую графічного планшета, щоб всі учні бачили правильну відповідь)

•    Графіком функції у = х² є ?
•    Областю визначення функції називаються?
•    Областю значень функції називаються?
• Нулями функції називають?
• Найбільшим значенням функції називають?
• Найменшим значенням функції називають?

Що учень бачить на екрані?

. Мотивація навчальної діяльності, повідомлення теми та мети уроку.

Тема нашого уроку - «Функція у=ах²+вх+с, а≠0,.її графік і властивості»

Вивчивши способи геометричних перетворень графіків функцій, можна побудувати графік будь-якої алгебраїчної функції.

На сьогоднішньому уроці ми розглянемо квадратичну функцію, графік якої можна утворити з графіка функції у = х², шляхом виконання одного або кількох геометричних перетворень.

Письмові вправи:

Вправа 1  №402 (Учень повинен звірити результат своєї роботи з тим, Що на екрані)

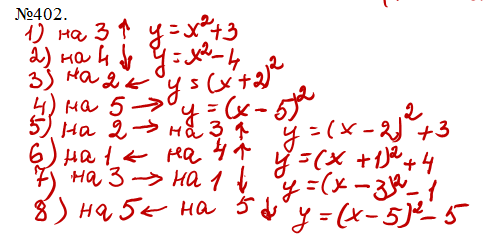
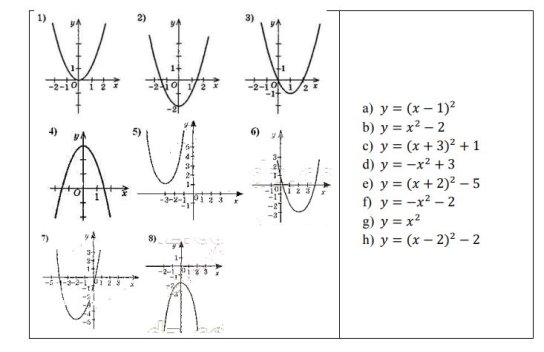
Вправа 2 Дано графіки функцій. Встановіть відповідність і помилки в невідповідності. (Усні пишуть номер і букву якій відповідає, якщо немає, пишуть повністю функцію)

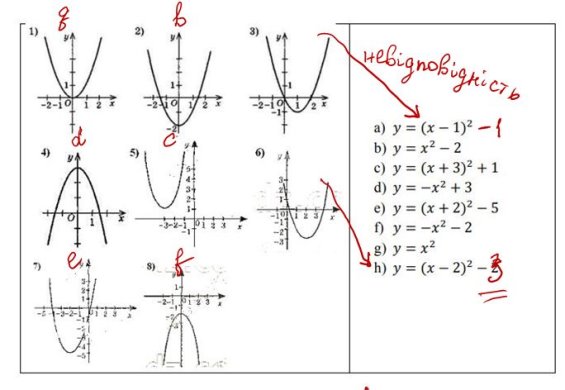
Вчитель   виводить результат.

Вправа 3 Розв’язати рівняння:

1. х²-2х=0,   2) х² - 3х + 2 = 0

Учні  після розв’язування перевіряють результат який вчитель виводить на екран.

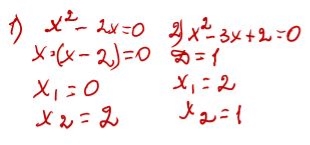
Вправа 4 Заповнити таблицю (Усно). Учні відповідають вчитель за допомогою планшета заповнює.

№	Квадратне рівняння:	Значення а	Значення Ь	Значення с	Дискримінант:	Визначити кількість коренів
1.	-3х2 - 4х + 2 = 0				D> 0
2.	х2 -2х + 1 = 0				D= 0
3.	3х2- 7х + 6 = 0				D < 0
4.	-х2 + 2х + 5 = 0				D > 0
5.	5х2-2х + 7 = 0				D< 0
6.	х2 + 10х + 4 = 0				D> 0
7.	х2 + 3х + 5 = 0				D< 0
8.	-4х2 + 12х + 9 = 0				D= 0
9.	х2 -5х = 0				—
10.	-х2 -2 = 0				—
11.	-х2 = 0				—
12.	х2 = 0				—

 

IV. Вивчення нового матеріалу.

План вивчення нового матеріалу

1.   Означення квадратичної функції.
2.    Графік квадратичної функції.
3.   Алгоритм побудови графіка функції у = ах² + Ьх + с.

V. Формування умінь і навичок.

(Під час пояснення нового матеріалу використовую фрагменти підручника, щоб учні зрозуміли на, що потрібно звернути увагу.)

Однією з найважливіших функцій є квадратична функція.

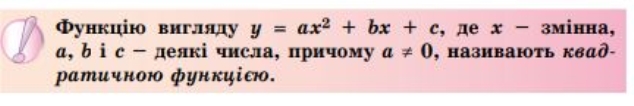
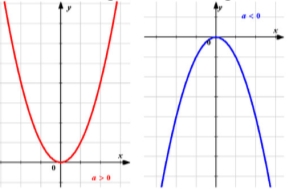
Якщо в=0, і с=0 тоді квадратична функція прийме вигляд у=ах². З даної функції ми розпочнемо. Спочатку побудуємо графіки. Буде два графіка при а>0 вітки параболи направлені вгору, при а<0 вітки параболи направлені вниз.

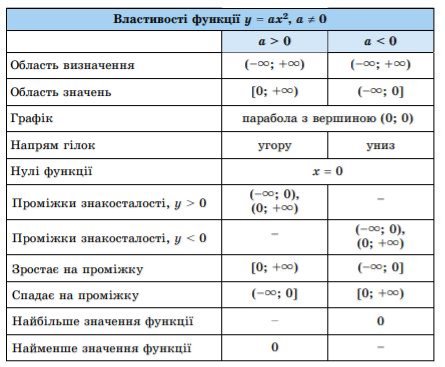
Систематизуємо властивості у вигляді таблиці і пояснимо їх.

Тепер розглянемо квадратичну функцію у = ах² + Ьх + с.

Графік функції у = ах² + Ьх + с можна отримати з графіка функції у = ах² за допомогою двох перетворень – перенесень уздовж координатних осей. Графіком функції у = ах² + Ьх + с є парабола з вершиною в точці (х_в;у_в), де х_в=; у_в=. Якщо а>0, гілки параболи направлені вгору, якщо а<0 – униз.

Будуючи графік функції у = ах² + Ьх + с, слід дотримуватися такої послідовності дій:

Систематизуємо властивості у вигляді таблиці.

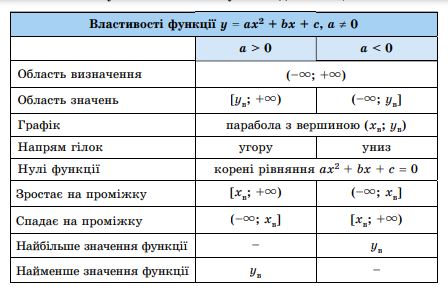
VI. Закріплення вивченого матеріалу.

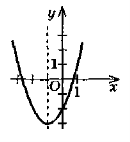Вправа 5.  На рисунку зображено графік функції у = ах² + Ьх + с. Використавши подані на рисунку умови, укажіть:

1.    знак числа а в рівнянні у = ах²+Ьх + с;
2.     координати вершини параболи;
3.     вісь параболи.

 

VII. Підсумки уроку.

Запитання до класу:

•      Скільки нулів має функція, якщо І) > 0, І) = 0, І) < 0
•      Який напрям мають вітки параболи, якщо а > 0 та а < 0
•      Як знайти вершину параболи і яке практичне застосування цієї формули VIII. Пояснення домашнього завдання.

Домашнє завдання

1.   Вивчити §11 ст.98.
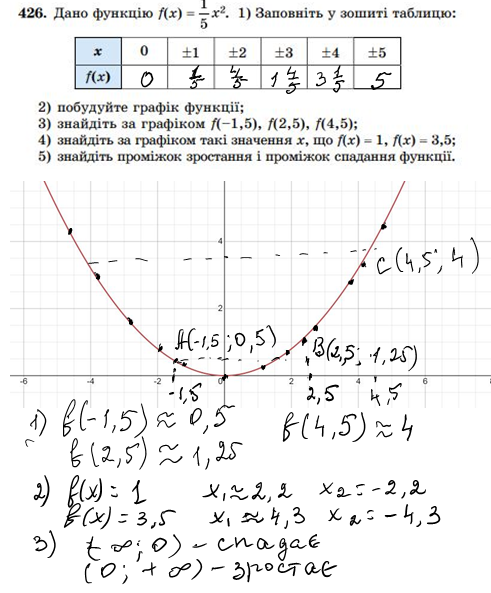
2.   Виконати №420, №427, №429. Користуйтеся даним конспектом прикріплений в Клас Румі.