Функція у = х2 її властивості, графік

Тема. Функція у = х² її властивості, графік

Мета: домогтися засвоєння учнями властивостей функції у = х² та виду і властивостей її графіка та способу застосування графіка функції у = х² для графічного розв'язання рівнянь виду х² = а; формувати вмін­ня відтворювати зміст вивчених понять, відпрацювати навички роботи з графіком функції.

Тин уроку: засвоєння знань та вмінь.

Хід уроку

1. Організаційний етап

На цьому етапі уроку слід надати учням інформацію про:

• орієнтовний план вивчення розділу;
• кількість навчальних годин;приблизний зміст матеріалу;
• основні вимоги до знань та вмінь учнів;
• приблизний зміст завдань, що будуть винесені на контроль.

(Цю інформацію можна помістити на стенді «Довідково-інформа­ційний куточок» у кабінеті математики та з метою економії часу запро­понувати учням для самостійного ознайомлення у позаурочний час).

2. Перевірка домашнього завдання

Якщо письмово було задано виконати аналіз контрольної роботи, то вчитель збирає зошити учнів для перевірки.

3. Формулювання мети і завдань уроку

Матеріал уроку певним чином пов'язаний з останньою темою попереднього розділу «Функція », а точніше із застосуванням побу­дови графіка цієї функції для графічного розв'язання рівнянь з однією змінною, що мають вигляд (де k ≠ 0, a, b — деякі числа. Тому певним поштовхом до вивчення матеріалу уроку може бути запропо­новане вчителем завдання:

«Не розв'язуючи рівняння, доведіть, що рівняння х² = а (де а — де­яке число) може мати або два, або один корінь, або не мати жодного кореня, залежно від значення числа а. Дослідіть цю залежність».

Таке формулювання завдання створює певну проблемну ситуацію, обговорюючи яку учні або самостійно, або за допомогою вчителя дохо­дять усвідомлення того, що єдиним на цей момент способом розв'язання задачі є спосіб, який учні опанували під час вивчення попередньої теми: тобто слід побудувати графіки двох функцій: у = х² та у = а і дослідити кількість точок перетину цих графіків залежно від значення числа а.

Таким чином, одним із головних постає питання про необхідність вивчення властивостей функції у = х² та побудову її графіка - це твер­дження виражає основну дидактичну мету уроку.

IV. Актуалізація опорних знань та вмінь

 З метою успішного сприйняття учнями навчального матеріалу уроку перед вивченням нового матеріалу слід активізувати такі знання і вміння учнів: основні поняття, пов'язані з поняттям функції та відповідними оперативними вміннями (для функції, заданої формулою? знайти: значення, функції, що відповідає значенню аргументу, та навпаки, знайти, при якому значенні аргументу функція набуває цих значень; перевірити, чи нале­жить точка із заданими координатами графіку функції, заданої формулою); вид графіка функції у = kх + b (та її особливий випа­док: у = b); виконання арифметичних дій з раціональними числами; означення та властивості степеня з натуральним по­казником (особливо властивість степеня з парним показником).

Виконання усних вправ

1. Знайдіть область визначення функції:

а) ; б) ; в) .

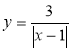2. Функцію задано формулою .

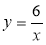а) Якого значення набуває функція, якщо аргумент дорівнює 4?

б) При якому значенні аргументу значення функції дорівнює ?

3. Чи проходить графік функції 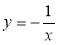через точки: а) А(-1; 1); б) В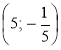; в) С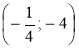; г) D?
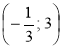4. Визначте знак виразу: а) (-3)¹⁰; б) (-x – 1)² ; в) -x² – 1.
5. Як називається графік функції 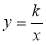при k ≠ 0? Опишіть властивості функції.
6. Опишіть вид графіка функції 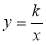(при k ≠ 0) при k > 0; k < 0.

V. Засвоєння знань

План вивчення нового матеріалу

1. Функція у = x²: її область визначення, область значень.
2. Графік функції у = х², його властивості.
3. Приклади задач на застосування властивостей функції у = х².

 Засвоєння знань учнями проводиться або у формі евристичної бесіди, або у формі пошукової роботи, метою якої є встанов­лення основних властивостей функції у = х² (області визначен­ня, області значень) та порівняння їх з основними властивостя­ми вивчених раніше функцій, а також встановлення форми графіка цієї функції (при цьому, так само як і під час вивчення питання про форму графіка функції , якщо є можливість, використати відповідні комп'ютерні програми), вивчення особ­ливостей цього графіка. Результати (висновки) цієї дослідниць­кої роботи заносяться до зошитів у вигляді таблиці (див. опор­ний конспект 8).

VI. Формування вмінь
Виконання усних вправ

1. Визначте без обчислення, які з точок не належать графіку функції у = х²: (-1; 1); (-2; -4); (0; 8); (3; -9); (1,7; 2,89); (16; 0). Відповідь поясніть.
2. Скільки спільних точок можуть мати пряма і графік функції у = х²?

а) Піднесіть до другого степеня: 3; -3; 0,5; ; 0; - 0,1;

б) Назвіть числа, квадрати яких дорівнюють: 36; 0,49; ; 1.

Виконання письмових вправ

Для досягнення мети уроку (див. вище) мають бути розв'язані вправи такого змісту:

1. Знаходження значень функції у = х² (аргументу), що відповідають даним значенням аргументу (функції) за формулою. Функцію задано формулою у = х². Знайдіть:

а) значення у, яке відповідає таким значенням х: - 4; - 2,1; 0; 5;

б) значення х, яким відповідають такі значення у: 36; 49; 100; 121.

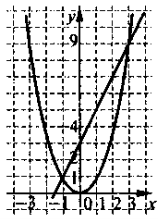2. Знаходження за готовим графіком функції у-х² значень функції (аргументу), що відповідають заданим значенням аргументу (функції).

Користуючись графіком функції у = х² (див. рис), знайдіть значення аргумен­ту, яким відповідають такі значення функції: 1,5; 3,5; 7,5.

3. Визначення, чи належить задана точка графіку функції у = х².

Чи   проходить   графік  функції   у = х²   через   точки:   A(15; 225); B(-22; 484); С ?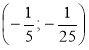

4. Побудова графіка функції у-х² разом із графіком якої-небудь
   функції (з вивчених раніше) та знаходження координат спільних
   точок цих графіків (точок перетину).

1. Побудуйте графік функції у = х², де -3 < х <2.

2) У скількох точках перетинаються графіки функцій:

а) у = х² і у = х – 5; б) у = х² і у = 4х – 4?

5. Графічне розв'язування рівнянь..

1. Розв'яжіть графічно рівняння: а) х² = - х + 2; б) х² – 3 = - 2х.
2. Знайдіть значення k, при якому графіки функцій у = kх + 4 і у = х² перетинаються в точці з абсцисою -1.

6. Логічні вправи та завдання підвищеного рівня складності для учнів,
   які мають достатній та високий рівень знань.

1. Знайдіть значення b, при якому графіки функцій у = 2х + b і у = х² мають лише одну спільну точку. Які координати цієї точки?
2. Користуючись графіком функції у = х¹, укажіть значення х, при яких точки параболи розміщені нижче від прямої у = - х + 6.
3. Знайдіть пропущений запис:

VII. Підсумки уроку

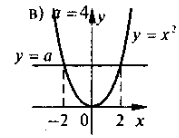
В якому з випадків правильно вказано значення параметра а?

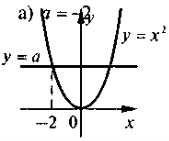
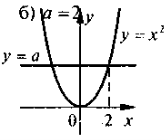
VIII. Домашнє завдання

1. Вивчити властивості функції у = х², схему побудови її графіка.
2. Розв'язати вправи, аналогічні за змістом до вправ класної роботи (для відпрацювання вмінь стосовно побудови графіка функції у = х² можна запропонувати виконання побудови графіка на міліметрово­му папері, звернувши особливу вагу учнів на поведінку графіка біля початку координат).
3. Повторити: означення степеня з натуральним показником, власти­вості парного степеня числа; розв'язати вправи на застосування цих понять.