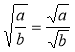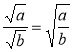Квадратний корінь з числа. Арифметичний квадратний корінь
Тема. Квадратний корінь з числа. Арифметичний квадратний корінь
Мета: домогтися засвоєння учнями змісту понять «квадратний корінь з числа», «означення арифметичного квадратного кореня з невід'ємного числа» та розуміння співвідношення між цими поняттями; сформувати в учнів уявлення про зміст запису ![]() та спосіб знаходження ОДЗ цього виразу; сформувати уявлення про спосіб розв'язання найпростіших ірраціональних рівнянь виду
та спосіб знаходження ОДЗ цього виразу; сформувати уявлення про спосіб розв'язання найпростіших ірраціональних рівнянь виду
![]()
на основі означення арифметичного квадратного кореня з невід'ємного числа; формувати первинні вміння здобувати арифметичний квадратний корінь із числа, знаходити ОДЗ найпростішого виразу, що містить арифметичний квадратний корінь, а також розв'язувати найпростіші ірраціональні рівняння.
Тин уроку: засвоєння знань та вмінь.
Наочність та обладнання: опорний конспект «Квадратний корінь та його властивості».
Хід уроку
I. Організаційний етап
II. Перевірка домашнього завдання
Перевірити виконання графічної частини домашнього завдання можна шляхом проведення невеликої тестової роботи № 5 із виконанням учнями (або готовими) графіків функції у = х2 (завдання на читання графіка та знаходження положення певних точок відносно побудованого графіка).
Тестова робота № 5
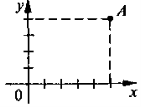
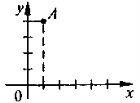
- Графіком якої з наведених функцій є парабола з вершиною в точці (0;0)?
|
А |
Б |
В |
Г |
|
у = х + 3 |
|
у = х2 |
у = х2 + 3 |
-
Функцію задано формулою у = х2. Знайдіть значення у, якщо х = -2
 .
.
|
А |
Б |
В |
Г |
|
4 |
- 4 |
|
6 |
- Яке твердження с неправильним?
|
А |
Б |
В |
Г |
|
Областю визначення функції у = х2 є всі числа |
Графіком функції у = х2 с парабола |
Точка (-1; 1) належить графіку функції у = х2 |
Функція у = х2 може набувати від'ємних значень |
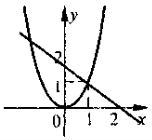
- Визначте рівняння, розв'язання якого зображено на рисунку?
|
А |
Б |
В |
Г |
|
х2 = х – 2 |
х2 = х + 2 |
х2 = 2х + 1 |
х2 = - х + 2 |
III. Формулювання мети і завдань уроку
З метою створення проблемної ситуації та відповідної мотивації діяльності учнів можна запропонувати завдання:
Розв'язати рівняння виду x + a = b, ax = b (відносно змінної х) та відповісти на запитання про спосіб обчислення коренів них рівнянь. х2 = а (якщо такі існують) для різних значень змінної (параметра) а.
Далі вчитель пропонує (посилаючись на знання учнів щодо кількості та існування коренів рівняння х2 = а, набуті на попередньому уроці) розв'язати рівняння виду х2 = а та відповісти на запитання про дію, яку слід виконати для відшукання коренів названого рівняння.
Усвідомлення проблеми, що при цьому виникає (учням поки що невідома дія, за допомогою якої можна знайти число, квадрат якого відомий), дозволяє вчителю за участі учнів сформулювати мету уроку: ознайомлення учнів з новою дією, що допоможе знайти число за значенням його квадрата (вивчення означення цієї дії та особливостей її виконання).
IV. Актуалізація опорних знань та вмінь
З метою успішного сприйняття учнями навчального матеріалу уроку перед вивченням нового матеріалу слід активізувати такі знання і вміння учнів: піднесення раціональних чисел до квадрата; застосування властивості степеня з парним показником; застосування властивостей функції у = х2 та властивостей її графіка; зміст поняття ОДЗ виразу та способи знаходження ОДЗ раціональних виразів.
Виконання усних вправ
- Піднесіть до другого степеня числа:
0; 2; -2; 0,3; ![]() ;
; ![]() ; 1
; 1![]() .
.
- Квадрати яких чисел дорівнюють:
0; 1; -0,2; ![]() ; 0,004?
; 0,004?
- Точка А(k; 6) належить графіку функції у = х2. Чи належить цьому графіку точки: В(k; -6); С(k; 6); М(-k; -6)? Відповідь обґрунтуйте.
-
Знайдіть ОДЗ виразу: 3х + 2;
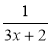 ;
; 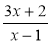 ;
; 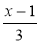 ;
; 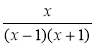 .
.
V. Засвоєння знань
План вивчення нового матеріалу
- Уявлення про квадратний корінь з невід'ємного числа як корінь рівняння х2 = а.
-
Означення арифметичного квадратного кореня з невід'ємного числа. ОДЗ виразу
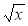 .
.
- Як обчислити значення арифметичного квадратного кореня з невід'ємного числа.
-
Як розв'язати рівняння
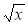 = a.
= a.
|
Конспект 9 |
|
Арифметичний квадратний корінь і його властивості |
|
1. Означення: |
|
а) якщо число х с коренем рівняння х2 = а, то х — квадратний корінь з числа а: |
|
б) якщо число х ≥ 0 є коренем рівняння х2 = а, то х — арифметичний квадратний корінь х числа а. |
|
Записують: |
|
Запам'ятай! Запис |
|
2. Властивості. Якщо а ≥ 0, b ≥ 0, то справджується рівність: |
|
а) |
|
б) якщо а ≥ 0 і b > 0, то |
|
в) для будь-яких а: |
|
г) |
|
3. Застосування |
|
а) Розв'язування рівняння |
|
|
|
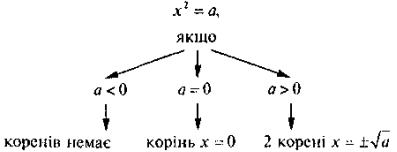
б) Розв'язування рівняння х2 = а: |
|
|
Традиційно формування уявлення учнів про зміст дії добування квадратного кореня проводиться на прикладі розв'язання задачі на знаходження коренів рівняння х2 = а, де а — певне число (бажано для можливості порівняння розглянути кілька прикладів, різних за знаком значень а, використовуючи при цьому уявлення учнів про властивості графіка функції у = х2). Тоді квадратними коренями називають саме корені рівняння х2 = а (а > 0). Після чого слід зауважити, що у випадку коли рівняння мас два корені, задача про знаходження квадратного кореня з додатного числа розв'язується неоднозначно, а це означає, то існує необхідність певною способу уточнення, про який саме квадратний корінь з додатного числа йде мова в задачі. Таким чином пояснюється необхідність уведення поняття арифметичного квадратного кореня з числа.
Означення арифметичного квадратною кореня з невід'ємного числа формулюється як у словесному вигляді (див. опорний конспект), так і у формі традиційної тотожності. Обговорюючи сформульоване означення, слід ще раз підкреслити, що операція добування квадратного кореня з числа виконується тільки для невід'ємних чисел (ОДЗ виразу ![]() є множина невід'ємних чисел).
є множина невід'ємних чисел).
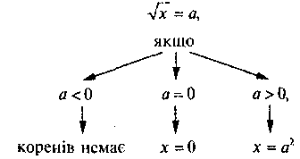
З означенням арифметичного квадратного кореня з невід'ємного числа тісно пов'язана схема розв'язання рівняння ![]() = а. При цьому слід показати учням, що так само, як і під час розв'язування рівняння х2 = а, наявність коренів залежить від знака числа а. Але, на відміну від рівняння х2 = а, корені рівняння
= а. При цьому слід показати учням, що так само, як і під час розв'язування рівняння х2 = а, наявність коренів залежить від знака числа а. Але, на відміну від рівняння х2 = а, корені рівняння ![]() = а знаходяться за означенням арифметичного квадратного кореня як квадрат значення цього кореня. Для кращого засвоєння учнями змісту цього фрагменту, схему розв'язання рівняння виду
= а знаходяться за означенням арифметичного квадратного кореня як квадрат значення цього кореня. Для кращого засвоєння учнями змісту цього фрагменту, схему розв'язання рівняння виду ![]() = а записуємо у вигляді алгоритму (див. опорний конспект).
= а записуємо у вигляді алгоритму (див. опорний конспект).
Важливо, щоб учні усвідомили різницю в поняттях квадратного кореня і арифметичного квадратного кореня (як у формі запису, так і у означеннях). Цьому сприятиме велика кількість розв'язаних на уроці і вдома різнопланових задач.
VI. Формування вмінь
Виконання усних вправ
- Знайдіть усі квадратні корені з чисел; арифметичний квадратний корінь із чисел: а) 49; б) 1; в) 0; г) - 25.
-
Доведіть, що: а)
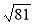 = 9; б)
= 9; б) 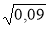 = 0,3; в)
= 0,3; в) 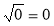 .
.
-
Чи має зміст вираз: а)
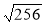 ; б)
; б) 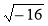 ; в)
; в) 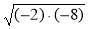 ?
?
-
Знайдіть квадрати чисел: 10; -8;
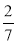 ; 0,9.
; 0,9.
- Знайдіть значення виразів при х = -5:
х2; (х – 2)2; (х + 1)2; (х + 4)2; |х|; |х – 5|; 2|х| – 3; ![]() ; |х| – 5; |х + 5|.
; |х| – 5; |х + 5|.
Виконання письмових вправ
Традиційно для письмового розв'язання на першому уроці вивчення означення квадратного кореня і арифметичного квадратного кореня пропонуються вправи такого змісту:
-
Доведення, що дане число є (або не є) значенням арифметичного
квадратного кореня з даного числа.
1) Доведіть, що:
а) число 5 є арифметичним квадратним коренем із 25;
б) число 0,3 є арифметичним квадратним коренем із 0,09;
в) число - 7 не є арифметичним квадратним коренем із 49;
г) число 0,6 не є арифметичним квадратним коренем із 3,6.
2) Доведіть, що: а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
3) Доведіть, що: а) ![]() ; б)
; б) ![]() .
.
4) Чи правильна рівність: а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ?
?
5) Доведіть, що: а) ![]() ; б)
; б) ![]() .
.
- Знаходження значення арифметичного квадратного кореня (виразу), що містить арифметичний квадратний корінь.
1) Обчисліть:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() ; д)
; д) ![]() ; є)
; є) ![]() ; ж)
; ж) ![]() ; з)
; з) ![]() .
.
2) Обчисліть: а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
3) Знайдіть значення виразу: а) ![]() +
+ ![]() ; б)
; б) ![]() ·
·![]() ;
;
в) ![]() ; г)
; г) ![]() ; д)
; д) ![]() ;
;
є) ![]() ; ж)
; ж) ![]() ; з)
; з) ![]() .
.
- Визначення, чи мас зміст вираз, що містить арифметичний квадратний корінь із числа.
1) Чи має зміст вираз: а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ?
?
2) При яких значеннях х має зміст вираз: а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ?
?
3) Чи має зміст вираз:
а) ![]() ; б)
; б) ![]() ; в)
; в) 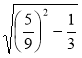 ?
?
-
Розв'язування рівнянь виду (або зводиться до виду)
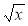 = а.
= а.
1) Чи існує значення змінної х, при якому:
а) ![]() = 0,1; б)
= 0,1; б) ![]() = – 10; в)
= – 10; в) ![]() + 1 = 0; г)
+ 1 = 0; г) ![]() – 3 = 0?
– 3 = 0?
2) Знайдіть значення змінної х, при якому правильна рівність:
а) ![]() ; б)
; б) ![]() ; в)
; в) 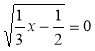 .
.
-
Логічні вправи та завдання підвищеного рівня складності для учнів,
які мають достатній та високий рівні знань.
1) Розв'яжіть рівняння:
а) 5![]() = 3; б)
= 3; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() ; д) 1 +
; д) 1 + ![]() = 10.
= 10.
2) Вставте пропущене число:
|
|
|
10 |
|
|
|
? |
Вправи, запропоновані для розв'язування на уроці, сприяють засвоєнню учнями означень квадратного кореня та арифметичного квадратного кореня (див. перший і другий вид завдань), засвоєнню знань про ОДЗ виразу ![]() та формуванню вмінь знаходити підкореневий вираз за означенням арифметичного квадратного кореня. У розв'язуванні вправ кожного виду неабияку роль відіграють знання учнями таблиці квадратів натуральних чисел та вміння застосовувати значення квадратів з цієї таблиці для піднесення до квадрата цілих та дробових чисел, а також подання раціональних чисел у вигляді квадрата деякого натурального або дробового чисел та вміння «впізнавати» такі числа. Тому впродовж вивчення цієї та інших тем курсу алгебри 8 класу корисно буде в систему усних вправ включити завдання на відпрацювання цих умінь (корисними для успішного подальшого вивчення алгебри для учнів є знання напам'ять значень квадратів натуральних чисел від 1 до принаймні 20).
та формуванню вмінь знаходити підкореневий вираз за означенням арифметичного квадратного кореня. У розв'язуванні вправ кожного виду неабияку роль відіграють знання учнями таблиці квадратів натуральних чисел та вміння застосовувати значення квадратів з цієї таблиці для піднесення до квадрата цілих та дробових чисел, а також подання раціональних чисел у вигляді квадрата деякого натурального або дробового чисел та вміння «впізнавати» такі числа. Тому впродовж вивчення цієї та інших тем курсу алгебри 8 класу корисно буде в систему усних вправ включити завдання на відпрацювання цих умінь (корисними для успішного подальшого вивчення алгебри для учнів є знання напам'ять значень квадратів натуральних чисел від 1 до принаймні 20).
VII. Підсумки уроку
В якому з випадків правильно виконано дію?
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() ; д)
; д) ![]() .
.
VIII. Домашнє завдання
- Вивчити означення квадратного кореня та арифметичного квадратного кореня, зміст властивостей та алгоритмів, вивчених на уроці.
- Розв'язати вправи на застосування вивчених понять (за змістом аналогічні до завдань класної роботи).
- Повторити: означення рівняння з однією змінною та зміст супутніх понять; графіки функцій у = а та у = х2; розв'язати завдання на побудову таких графіків.


про публікацію авторської розробки
Додати розробку