Рівняння х2 = а. Основна тотожність квадратного кореня.
Тема. Рівняння х2 = а. Основна тотожність квадратного кореня.
Мета: повторити та узагальнити знання учнів щодо способу розв'язання рівняння виду х2 = а (записати алгоритм розв'язання рівняння із використанням знань учнів про арифметичний квадратний корінь з невід'ємного числа); використовуючи означення арифметичного квадратного кореня з невід'ємного числа, сформулювати основну тотожність для квадратного кореня; формувати вміння з використанням записаного алгоритму розв'язувати рівняння виду х2 = а, а також рівняння, що зводяться до таких шляхом рівносильних перетворень; використовувати записану тотожність для квадратного кореня для більш раціонального обчислення значень числових виразів, що містять квадратний корінь.
Тин уроку: повторення та узагальнення знань, застосування знань та вмінь.
Наочність та обладнання: опорний конспект «Квадратний корінь та його властивості».
Хід уроку
I. Організаційний стан
II. Перевірка домашнього завдання
В учнів, які потребують додаткової педагогічної уваги, вчитель перевіряє виконання домашнього завдання, зібравши зошити на перевірку.
Усі учні можуть у разі необхідності (якщо на попередньому уроці самостійна робота була виконана не дуже вдало) виконати корекційну роботу або тестове завдання відповідного змісту.
III. Формулювання мети і завдань уроку
Для встановлення мети уроку достатньо пригадати разом з учнями, які поняття було вивчено на попередніх уроках цього розділу, та спробувати встановити логіку вивчення матеріалу: від уявлення про кількість коренів рівняння х2 = а (на основі уявлення про графік функції у = х2 та можливості його застосування для розв'язування рівнянь з однією змінною графічним способом) – до уявлення про дію над невід'ємними числами, обернену до піднесення до 2-го степеня (добування квадратного кореня з невід'ємного числа).Серед інших питань, які можуть виникнути під час розгляду цього логічного ланцюжка, передбачаємо такі:
- як знайти корені рівняння х2 = а, використовуючи дію добування квадратного кореня з числа;
- як ще можна використати означення арифметичного квадратного кореня з числа?
Відшукання відповіді на ці питання і становитиме мету уроку.
IV. Актуалізація опорних знань та вмінь
З метою успішного сприйняття учнями навчального матеріалу уроку перед вивченням нового матеріалу слід активізувати такі знання і вміння учнів: найбільш вживані значення квадратів раціональних чисел; добування коренів з раціональних чисел; графічні уявлення про кількість розв'язків рівняння х2 = а; основна властивість степеня з цілим показником та її наслідків (зокрема властивості щодо піднесення до степеня добутку), а також властивість парного степеня від'ємного числа.
Виконання усних вправ
- Визначте сторони квадрата, площа якого дорівнює:
36 см2; 0,81 дм2; 1 м2; 900 мм2?
-
Обчисліть АКК із чисел: 4; 9; 0,25; 0,81; 0,64;
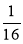 ;
; 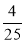 ;
; 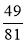 ; 3
; 3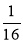 .
.
- Скільки спільних точок має графік функції у = х2 із прямою:
а) у = 4; б) у = 0,9; в) у = 0; г) у = -2; д) y = 3?
V. Застосування знань
План вивчення нового матеріалу
-
Доведення того, то при а > 0 корені рівняння х2 = а х1 і х2 дорівнюють відповідно
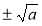 .
.
- Загальна схема розв'язання рівняння х2 = а.
- Формулювання та доведення основної тотожності для квадратного кореня.
Традиційно уявлення про існування та спосіб знаходження коренів рівняння х2 = а формується у процесі роботи з графіками функцій у = а (а — будь-яке число) та у = х2, при цьому спочатку повторюються загальні уявлення про можливу кількість коренів (див. урок 33), а вже потім здійснюється перехід до точного знаходження цих коренів, якщо вони існують. Саме по собі доведення твердження, що при а > 0 коренями рівняння х2 = а є числа ![]() , дають лише можливість записати розв'язки рівняння. Щоб усвідомити, що при а > 0 корені рівняння х2 = а, по-перше, існуватимуть і, по-друге, завжди будуть протилежними числами, слід знову звернутись до графічних образів і на них продемонструвати справедливість цих тверджень. Після констатації цього факту доречно хоча б на рівні ознайомлення показати учням, що корені рівняння (тобто вирази виду
, дають лише можливість записати розв'язки рівняння. Щоб усвідомити, що при а > 0 корені рівняння х2 = а, по-перше, існуватимуть і, по-друге, завжди будуть протилежними числами, слід знову звернутись до графічних образів і на них продемонструвати справедливість цих тверджень. Після констатації цього факту доречно хоча б на рівні ознайомлення показати учням, що корені рівняння (тобто вирази виду ![]() при а > 0) можуть бути не тільки раціональними (тобто створюється певна мотивація діяльності на наступний урок).
при а > 0) можуть бути не тільки раціональними (тобто створюється певна мотивація діяльності на наступний урок).
Після вивчення питання про застосування означення арифметичного квадратного кореня з невід'ємного числа для розв'язування рівняння х2 = а вивчається питання про застосування цього самого означення для перетворення виразу виду ![]() (при a ≥ 0). Доведення цієї тотожності не повинно викликати в учнів труднощів (бо здійснюється цілком на основі означення арифметичного квадратного кореня з числа), але застосування цієї властивості разом із властивістю степеня про піднесення до степеня добутку зазвичай викликає певні труднощі в учнів. Тому після формулювання та доведення основної тотожності для арифметичного квадратного кореня слід розглянути (розібрати та записати розв'язання) кілька прикладів відповідного змісту.
(при a ≥ 0). Доведення цієї тотожності не повинно викликати в учнів труднощів (бо здійснюється цілком на основі означення арифметичного квадратного кореня з числа), але застосування цієї властивості разом із властивістю степеня про піднесення до степеня добутку зазвичай викликає певні труднощі в учнів. Тому після формулювання та доведення основної тотожності для арифметичного квадратного кореня слід розглянути (розібрати та записати розв'язання) кілька прикладів відповідного змісту.
VI. Формування вмінь
Виконання усних вправ
- Скільки коренів мають рівняння:
х2 = 9; х2 = -9; х2 = 3; х2 = 0; х2 – 31 = 0; х2 = – 31?
-
Із рівнянь виберіть ті, які мають два протилежних:
а) раціональних корені; б) ірраціональних корені:
х2 = 16; х2 – 7 = 0; х2 + 3= 0; х2 – 0,25 = 0; 0,6 – х2 = 0; – х2 – 5 = 0.
- Знайдіть корені рівнянь:
х2 = 16; у2 = 0,81; z2 = -4; m2 = 5; n2 = ![]() ; d2 = π.
; d2 = π.
Виконання письмових вправ
Для досягнення основної мети уроку письмово слід розв'язати вправи такого змісту:
- Визначення, чи має рівняння корені, якщо має, то скільки.
1) Наведіть приклад рівняння вигляду х2 = а, яке:
а) має два раціональні корені; б) має два ірраціональні корені;
в) не має коренів.
2) Чи має корені рівняння:
а) х2 = 81; б) х2 = 18; в) х2 = 0; г) х2 = -25?
- Розв'язування рівнянь виду х2 = а аналітично і графічно.
1) Розв'яжіть рівняння: а) х2 = 121; б) х2 = 0,16; в) х2 = 5; г) х2 = 0,3;
д) х2 = ![]() ; є) х2 =
; є) х2 = ![]() ; ж) х2 = -1; з) х2 = 1,44.
; ж) х2 = -1; з) х2 = 1,44.
2) Розв'яжіть рівняння:
а) 3х2 = 48; б) х2 + 8 = 57; в) 44 – х2 = 8; г) -2х2 = 18; д) -0,4х2 = -8;
є) ![]() х2 = 1; ж) 12 + 3х2 = 6; з) 2(х2 + 1) = 10.
х2 = 1; ж) 12 + 3х2 = 6; з) 2(х2 + 1) = 10.
3) Розв'яжіть рівняння за допомогою графіка функції у = х2, знайдіть наближенні значення його коренів:
а) х2 = 3; б) х2 = 5; в) х2 = 4,5; г) х2 = 8,5.
- Розв'язування рівнянь, що зводяться до виду х2 = а.
1) Розв'яжіть рівняння: а) 2(х2 – 3) + 3(2х2 + 1) = 5;
б) (2х – 5)2 + (2х + 5)2 = 62; в) ![]() ; г) (5х + 1)2 – 2 = 10х.
; г) (5х + 1)2 – 2 = 10х.
2) Розв'яжіть рівняння:
а) (х – 3)2 = 25; б) (х + 4)2 = 9; в) (х – 6)2 = 7; г) (х + 2)2 = 6.
- Розв'язування рівняння х2 = а з параметром.
-
Знаходження значень виразів вигляду
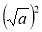 та
та 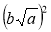 , де a ≥ 0.
, де a ≥ 0.
1) Знайдіть значення виразу: а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
2) Знайдіть значення виразу: а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ;
;
г) ![]() ; д) 0,5
; д) 0,5![]() ; є)
; є) ![]() ; ж)
; ж) 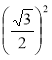 ; з)
; з) 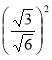 .
.
-
Логічні вправи та завдання підвищеного рівня складності для учнів,
які мають достатній та високий рівні знань.
1) Знайдіть значення виразу:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ;
;
г) ![]() +
+![]() ; д)
; д) ![]() ; с)
; с) ![]() .
.
2) При яких значеннях а і b має зміст вираз:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() ; д)
; д) ![]() ?
?
3) Яке з даних чисел слід вилучити:
![]() ; 1,9;
; 1,9; ![]() ; 1,3;
; 1,3; ![]() ;
; ![]() ?
?
-
На повторення: розв'язати рівняння
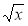 = а.
= а.
1) Розв'яжіть рівняння:
а) ![]() = 8; б)
= 8; б) ![]() = 1; в)
= 1; в) ![]() = - 4; г)
= - 4; г) ![]() ; д)
; д) ![]() ;
;
є) ![]() + 9 = 7; ж)
+ 9 = 7; ж) ![]() з)
з) ![]() ; и)
; и) ![]() .
.
2) Розв'яжіть рівняння: а) ![]() ; б)
; б) ![]() ;
;
в) ![]() +
+![]() = 0; г)
= 0; г) ![]() +
+![]() = 0.
= 0.
Основний зміст письмових вправ складають вправи на формування вмінь застосовувати схему розв'язання рівняння х2 = а та рівнянь, що зводяться до такого виду шляхом тотожних перетворень або заміною змінних (можна в неявному вигляді), а також вправи на закріплення знання та застосування основної властивості для квадратного кореня (при цьому на розв'язування рівнянь робиться більший акцент). Після відпрацювання умінь безпомилково застосовувати схему розв'язання рівнянь х2 = а в ситуаціях різного рівня складності доречно виконати кілька вправ на розв’язування рівнянь виду ![]() = а (вивчених на попередньому уроці), після чого зробити порівняльний аналіз схем розв'язання цих видів рівнянь (досвід показує, що учні часто-густо плутають ці схеми).
= а (вивчених на попередньому уроці), після чого зробити порівняльний аналіз схем розв'язання цих видів рівнянь (досвід показує, що учні часто-густо плутають ці схеми).
І наостанок, у разі успішного опанування питання про розв'язання рівняння х2 = а, можна запропонувати до уваги учнів найпростіші рівняння виду х2 = а з параметром.
VII. Підсумки уроку
В якому з випадків правильно розв'язано рівняння?
|
а) х2 – 5 = 0, -5 < 0 |
б) х2 – 5 = 0, х2 = 5, |
в) х2 – 5 = 0, х2 = 5, |
|
коренів немає. |
х = |
х = |
|
Відповідь. Коренів немає |
Відповідь. |
Відповідь. |
VIII. Домашнє завдання
- Вивчити теоретичний матеріал уроку (див. конспект).
- Розв'язати завдання таких видів, як і в класній роботі.
- Повторити: властивості степеня з натуральним показником (див. 7 клас), виконати вправи на застосування цих властивостей.


про публікацію авторської розробки
Додати розробку
