Квадратний корінь з числа. Арифметичний квадратний корінь
Тема. Квадратний корінь з числа. Арифметичний квадратний корінь
Мета: закріпити знання учнів про зміст понять «квадратний корінь з числа», «означення арифметичного квадратного кореня з невід'ємного числа», про зміст запису ![]() та спосіб знаходження ОДЗ цього виразу, про спосіб розв'язання найпростіших ірраціональних рівнянь виду
та спосіб знаходження ОДЗ цього виразу, про спосіб розв'язання найпростіших ірраціональних рівнянь виду ![]() на основі означення арифметичного квадратного кореня з невід'ємного числа; удосконалити вміння добувати арифметичний квадратний корінь із числа, знаходити ОДЗ найпростішого виразу, що містить арифметичний квадратний корінь, а також розв'язувати найпростіші ірраціональні рівняння; здійснити діагностику засвоєння учнями названого вите матеріалу.
на основі означення арифметичного квадратного кореня з невід'ємного числа; удосконалити вміння добувати арифметичний квадратний корінь із числа, знаходити ОДЗ найпростішого виразу, що містить арифметичний квадратний корінь, а також розв'язувати найпростіші ірраціональні рівняння; здійснити діагностику засвоєння учнями названого вите матеріалу.
Тип уроку: застосування знань та вмінь.
Наочність та обладнання: опорний конспект «Квадратний корінь та його властивості».
Хід уроку
I. Організаційний етап
II. Перевірка домашнього завдання
Якщо на попередньому уроці учні добре засвоїли навчальний матеріал, то перевірку домашнього завдання можна провести у формі ігрового моменту («Знайди помилку»).
Якщо ж під час виконання домашнього завдання в учнів виникли труднощі, перевірку домашнього завдання проводимо у формі перевірки за зразком.
У цьому разі «сильні» учні (під час перевірки домашнього завдання) можуть виконувати індивідуальні завдання.
III. Формулювання мети і завдань уроку
Проведена перевірка виконання домашнього завдання та аналіз можливих помилок самі по собі створюють мотивацію учнів до діяльності з усунення причини помилок (корекції знань), а також вдосконалення вмінь. Тому саме корекція знань учнів щодо змісту означення квадратного кореня з числа та арифметичного квадратного кореня з невід'ємного числа й відпрацювання вмінь учнів застосовувати вивчене означення для добування кореня з невід'ємного числа, знаходження ОДЗ виразу, що містить арифметичний квадратний корінь з числа, та для розв'язування найпростіших ірраціональних рівнянь і становлять основну дидактичну мету уроку.
IV. Актуалізація опорних знань та вмінь
З метою успішного сприйняття учнями навчального матеріалу уроку перед вивченням нового матеріалу слід активізувати такі знання і вміння учнів: обчислення значень квадратів раціональних чисел, розв'язування лінійних рівнянь з однією змінною, арифметичні дії з раціональними числами, обчислення значень виразів зі змінними при заданих значеннях змінної, а також зміст означення арифметичного квадратного кореня з невід'ємного числа.
Виконання усних вправ
- Знайдіть значення виразів:
72; (-7)2; -72; ![]() ;
; 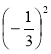 ; (-11)2;
; (-11)2; ![]() ; (-0,3)2; 202; (-30)2; 0,42; (-0,8)2.
; (-0,3)2; 202; (-30)2; 0,42; (-0,8)2.
- Чи правильне твердження:
а) ![]() = ± 54; б)
= ± 54; б) ![]() = 0,6; в)
= 0,6; в) ![]() = -0,6; г)
= -0,6; г) ![]() = 0,9?
= 0,9?
-
Обчисліть:
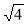 ;
; 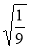 ;
; 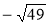 ;
; 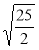 ;
; 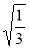 ;
; 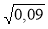 ;
; 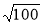 ;
; 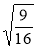 .
.
V. Застосування вмінь
Виконання письмових вправ
Для реалізації дидактичної мети на цьому уроці, як і на попередньому, слід розв'язати завдання такого змісту.
- Доведення, що дане число є (або не є) значенням арифметичного квадратного кореня з даного числа.
Доведіть, що: а) ![]() = 19; б)
= 19; б) ![]() = 0,11.
= 0,11.
- Знаходження значення арифметичного квадратного кореня (виразу, що містить арифметичний квадратний корінь).
1) Знайдіть значення виразу:
а) ![]() , якщо х = 3; х = - 1; х = 0,12;
, якщо х = 3; х = - 1; х = 0,12;
б) ![]() , якщо а = 8, b = 2; а = -3, b = -14.
, якщо а = 8, b = 2; а = -3, b = -14.
2) Знайдіть з допомогою таблиці квадратів значення квадратного кореня: а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
3) Знайдіть значення виразу: а) 10![]() + 4
+ 4![]() ;
;
б) 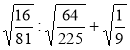 ; в)
; в) ![]() ; г)
; г) ![]() ;
;
д) ![]() ; є)
; є) 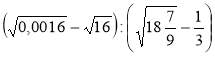 .
.
- Визначення, чи має зміст вираз, що містить арифметичний квадратний корінь із числа.
1) Чи має зміст вираз:
а) ![]() ; б)
; б) ![]() ; в)
; в) 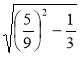 ?
?
-
Логічні вправи та завдання підвищеного рівня складності для учнів,
які мають достатній та високий рівні знань.
1) Укажіть допустимі значення змінної х.
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() ; д)
; д) ![]() ; є)
; є) ![]() .
.
2) При яких значеннях змінної має зміст вираз:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ?
?
3) Знайдіть пропущене число:
|
|
|
|
|
? |
-
Розв'язування рівнянь виду (або яке зводиться до виду)
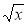 = а.
= а.
Розв'яжіть рівняння ![]() .
.
Вправи, запропоновані для розв'язування на уроці, сприяють закріпленню означень квадратного кореня з числа та арифметичного квадратного кореня з невід'ємного числа, знань про ОДЗ виразу ![]() та вдосконаленню вмінь знаходити підкореневий вираз за означенням АКК (розв'язувати рівняння виду
та вдосконаленню вмінь знаходити підкореневий вираз за означенням АКК (розв'язувати рівняння виду ![]() = а) і відтворюють ситуації, розглянуті на попередньому уроці, але на більш високому рівні складності.
= а) і відтворюють ситуації, розглянуті на попередньому уроці, але на більш високому рівні складності.
VII. Підсумки уроку
Тестова робота № 6
- Яка рівність с правильною?
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Обчисліть:
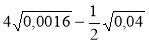 .
.
|
А |
Б |
В |
Г |
|
0,06 |
0,006 |
0,15 |
0,0015 |
-
Знайдіть значення виразу
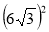 .
.
|
А |
Б |
В |
Г |
|
36 |
108 |
54 |
18 |
-
Укажіть усі значення змінної х, при яких вираз
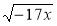 має зміст.
має зміст.
|
А |
Б |
В |
Г |
|
х > 0 |
х < 0 |
х = 0 |
х ≤ 0 |
-
Розв'яжіть рівняння
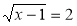 .
.
|
А |
Б |
В |
Г |
|
3 |
1 |
5 |
-3 |
VIII. Домашнє завдання
- Повторити означення квадратного кореня з числа, арифметичного квадратного кореня з числа, зміст властивостей та алгоритмів, вивчених на уроці.
- Розв'язати вправи на застосування вивчених понять (змісту та рівня, аналогічного до змісту та рівня завдань класної роботи).
- Повторити: означення рівняння з однією змінною та зміст супутніх понять; графіки функцій у = а та у = х2; розв'язати завдання на побудову таких графіків.

про публікацію авторської розробки
Додати розробку
