Раціональні числа, ірраціональні числа, дійсні числа, числові множини, етапи розвитку числа.
Тема. Раціональні числа, ірраціональні числа, дійсні числа, числові множини, етапи розвитку числа.
Мета: систематизувати, узагальнити знання учнів щодо поняття числа та видів чисел, сформувати уявлення про множину дійсних чисел; сформувати вміння учнів відтворювати означення та властивості видів чисел, вивчених на уроці, виконувати найпростіші дії з дійсними числами (зокрема порівняння), використовувати вивчені властивості та означення для розв'язування задач на класифікацію чисел та доведення того факту, що дане число є числом певного виду, знаходити наближені значення квадратних коренів із чисел за чотиризначними математичними таблицями.
Тип уроку: застосування знань та вмінь.
Наочність та обладнання: опорний конспект «Дійсні числа».
Хід уроку
I. Організаційний етап
II. Перевірка домашнього завдання
Перевірку виконання домашнього завдання в разі необхідності (якщо на попередньому уроці учні не дуже добре засвоїли матеріал) проводимо за методикою перевірки за зразком. У цьому разі учням, які добре засвоїли матеріал, пропонується індивідуальне завдання.
Якщо на попередньому уроці всі учні добре опанували навчальний матеріал, то виконується тестове завдання.
Тестове завдання № 7
- Розв'яжіть рівняння х2 – 21 = 0.
|
А |
Б |
В |
Г |
|
21 |
|
Коренів немає |
0 |
- Знайдіть корінь рівняння 3у2 – 4,8 = 0.
|
А |
Б |
В |
Г |
|
0,4 |
|
|
Коренів немає |
-
Виберіть правильне твердження. Рівняння
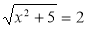 .
.
|
А |
Б |
В |
Г |
|
не має жодного кореня |
має один раціональний корінь |
мас два ірраціональні корені |
має один ірраціональний корінь |
III. Формулювання мсти і завдань уроку
З метою створення відповідної мотивації діяльності учнів учитель пропонує учням завдання:
Розв'яжіть рівняння: х2 = 9, х2 = -1, х2 = 2. Виконайте зображення чисел, що є коренями цих рівнянь, на числовій прямій.
Виконання завдання створює певне протиріччя між знаннями учнів (вони знають, що при будь-якому а > 0 рівняння х2 = а має два корені) та неможливістю їх застосування (учні не знають, що являють собою числа ![]() , отже, не знають, як їх побудувати на координатній прямій).
, отже, не знають, як їх побудувати на координатній прямій).
Означення цих чисел, вивчення їх найпростіших властивостей та з'ясування того, в яких логічних відношеннях знаходяться ці числа з відомими учням числами, складають основну дидактичну мету уроку.
IV. Актуалізація опорних знань та вмінь
З метою успішного сприйняття учнями навчального матеріалу уроку перед вивченням нового матеріалу слід активізувати такі знання і вміння учнів: виконання арифметичних дій з раціональними числами; піднесення до квадрата, і навпаки, добування квадратного кореня з деяких раціональних чисел; знаходження допустимих значень виразів, що містять квадратний корінь із числа; розв'язування рівнянь виду х2 = а, а також застосування основної тотожності для квадратного кореня.
Виконання усних вправ
-
Знайдіть значення виразів: 72; (-7)2 ; -72;
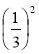 ;
; 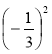 ; (-11)2; 02.
; (-11)2; 02.
-
Обчисліть:
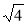 ;
; 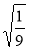 ;
; 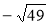 ;
; 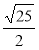 ;
; 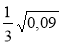 ;
; 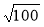 ;
; 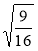 ;
; 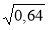 .
.
- Розв'яжіть рівняння: а2 = 16; у2 = 0,81; х2 = -4; х2 = 5, с2 = 8.
V. Застосування знань
План вивчення нового матеріалу
- Систематизація відомостей учнів про числові множини, відомі учням з курсу 5—6 класів.
- Уявлення про раціональні числа, ірраціональні числа. Порівняння раціональних та ірраціональних чисел.
- Співвідношення між вивченими числовими множинами.
- *Знаходження наближених значень квадратних коренів за чотиризначними математичними таблицями.
На цьому уроці теми «Квадратні корені» уточнюються наявні в учнів уявлення про числові множини (поняття числової множини сприймається учнями на інтуїтивному рівні). У ході вивчення навчального матеріалу уроку учні мають повторити означення видів чисел, вивчених у попередніх класах (натуральні числа – це числа, що застосовуються при лічбі, цілі – це натуральні, їм протилежні числа і нуль, раціональні числа – це числа, які можна подати у вигляді ![]() , де т — ціле число, а п — натуральне), та співвідношення між множинами цих чисел (будь-яке натуральне число є цілим, будь-яке ціле число – раціональне).
, де т — ціле число, а п — натуральне), та співвідношення між множинами цих чисел (будь-яке натуральне число є цілим, будь-яке ціле число – раціональне).
Для уведення поняття дійсного числа існують різні підходи, однак усі вони достатньо складні для восьмикласників. Тому в курсі 8 класу обмежуються лише початковими, найбільш зрозумілими уявленнями про множини дійсних чисел та підмножини – множини раціональних та ірраціональних чисел (множина ірраціональних чисел є доповненням множини раціональних чисел до множини дійсних чисел).
Повторивши означення та властивості раціональних чисел (будь-яке раціональне число можна подати у вигляді нескінченного періодичного десяткового дробу — див. «Математика, 6 клас», автори: Мерзляк А. Г., Полонський В. Б., Якір М. С.), учні знайомляться з поняттям нескінченного неперіодичного десятковою дробу (традиційно в цьому місці наводиться приклад, єдиного, відомого учням на цей момент, ірраціонального числа — число л); в учнів формується уявлення про ірраціональне число. При цьому важливо підкреслити: ірраціональні числа — свого роду антипод раціональних чисел (раціональні числа можна подати у вигляді нескінченних періодичних десяткових дробів, а ірраціональні числа, навпаки, можна подати у вигляді нескінченних неперіодичних десяткових дробів).
На цьому етапі розглядається питання про означення виду чисел ![]() (учні мають зрозуміти, що ці числа, а також подібні до таких числа, є прикладами ірраціональних чисел) та їх побудову (на жаль, з причини недосконалості програми, побудова відрізка, довжина якого дорівнює ірраціональному числу виду
(учні мають зрозуміти, що ці числа, а також подібні до таких числа, є прикладами ірраціональних чисел) та їх побудову (на жаль, з причини недосконалості програми, побудова відрізка, довжина якого дорівнює ірраціональному числу виду ![]() , переноситься на той час, коли на уроках геометрії вивчатиметься теорема Піфагора — див. Програма з геометрії, 8 клас).
, переноситься на той час, коли на уроках геометрії вивчатиметься теорема Піфагора — див. Програма з геометрії, 8 клас).
Після чого доречно буде нагадати учням відомі їм правила порівняння раціональних чисел та на їх основі скласти правила порівняння ірраціональних чисел. При цьому акцент робиться на тому, що оскільки ірраціональні числа подаються тільки у вигляді нескінченного неперіодичного десяткового дробу, то, виконуючи порівняння ірраціональних чисел, зазвичай використовують їх наближені значення з певною кількістю перших значущих цифр у їх записах. Атому цілком логічно буде ознайомити учнів принаймні зі способом знаходження наближених значень квадратних коренів і використанням чотиризначних математичних таблиць.
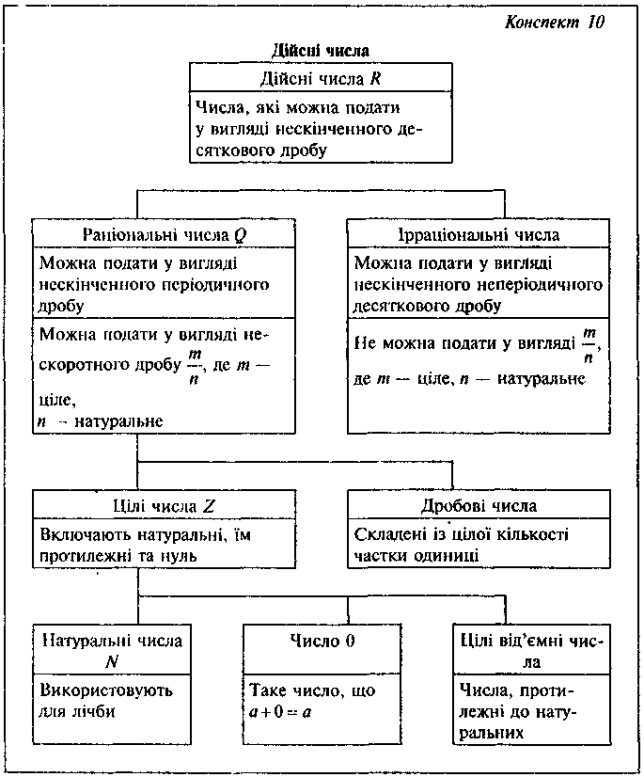
На закінчення вивчення матеріалу формується уявлення про числову множину, що складається з множин раціональних та ірраціональних чисел — множину дійсних чисел, і узагальнюється уявлення учнів про співвідношення між названими числовими множинами (наочне уявлення про це співвідношення традиційно дається на кругах Ейлера або у вигляді схеми - див. опорний конспект 10).
VI. Формування вмінь
Виконання усних вправ
- Наведіть приклади чисел, які є: а) цілими від'ємними; б) раціональними додатними; в) цілими невід'ємними.
- Чи правда, що: а) будь-яке ціле число є дійсним;
б) будь-яке ірраціональне число є дійсним;
в) будь-яке дійсне число є раціональним?
- Укажіть правильне твердження:
а) π — число дійсне; б) 2,222... — число раціональне;
в) 2,212211222111... — число раціональне; г) - 2 — число дійсне.
Виконання письмових вправ
Для досягнення основної мсти уроку письмово слід розв'язати вправи такого змісту:
-
Усвідомлення означень різних видів дійсних чисел; раціонального
числа та ірраціонального числа.
1) Наведіть приклад:
а) раціонального числа; б) ірраціонального числа.
2) Серед чисел ![]() ; 0; 0,25; -2,(3); 0,818118111... (кількість одиниць, яка ділить вісімки, кожний раз збільшується на 1); 4,2(51); 217; π укажіть раціональні та ірраціональні.
; 0; 0,25; -2,(3); 0,818118111... (кількість одиниць, яка ділить вісімки, кожний раз збільшується на 1); 4,2(51); 217; π укажіть раціональні та ірраціональні.
-
Порівняння раціональних та ірраціональних чисел; на виконання
дій із раціональними числами.
1) Порівняйте числа: а) 8,998... і 9,113; б) -0,382... і 5,117...;
в) -32,144... і -12,543...; г) -2,724... і -2,725...
2) Яке з чисел більше:
а) 0,6 чи ![]() ; б) -0,327 чи
; б) -0,327 чи ![]() ; в) 0,579... чи 0,58;
; в) 0,579... чи 0,58;
г) 2,72 чи 2,(72); д) 1,7 чи ![]() ; є) 1,8 чи
; є) 1,8 чи ![]() ; ж)
; ж) ![]() чи -3; з)
чи -3; з) ![]() чи -2?
чи -2?
3) Запишіть у порядку зростання числа: 2,(7); 0,82; -1,95...; -0,03...; ![]() .
.
4) Знайдіть наближене значення суми х + у, округливши доданки до
сотих: а) х = 3,849.., у =1,1020...; б) х = 102,3120..., у =23,1023...
- Вправи, що передбачають формування вмінь учнів працювати з чотиризначними математичними таблицями (квадратних коренів).
Порівняйте числа: а) ![]() і
і ![]() ; б) 2
; б) 2![]() і
і ![]() ; в)
; в) ![]() і -1,4(3).
і -1,4(3).
-
Вправи на доведення того, то задане число с ірраціональним. Доведіть, що
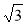 — ірраціональне число.
— ірраціональне число.
- Логічні вправи та завдання підвищеного рівня складності для учнів, які мають достатній та високий рівні знань.
1) Дано числа: -25; 3,8; 8; 0; -2,1; ![]() ;
; ![]() ; 0,(6);
; 0,(6); ![]() ; 1; -2
; 1; -2![]() ; π; 0,10110111011110... (кількість одиниць послідовно збільшується на 1). Випишіть:
; π; 0,10110111011110... (кількість одиниць послідовно збільшується на 1). Випишіть:
а) усі натуральні числа; б) усі цілі числа; в) усі раціональні числа; г) усі ірраціональні числа.
2) Вставте пропущений вираз:
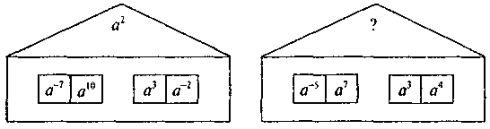
- На повторення: розв'язування рівнянь виду х2 = а, найпростіших ірраціональних рівнянь та таких, що зводяться до названих видів (шляхом найпростіших рівносильних перетворень).
1) Знайдіть значення змінної х, при якому Правильна рівність:
а) ![]() ; б)
; б) ![]() ; в)
; в) 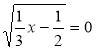 .
.
2) При яких значеннях а рівняння має один корінь:
а) х2 = а2 – 2а; б) ![]() ?
?
Вправи зазначеного змісту сприяють закріпленню означень раціонального та ірраціонального чисел, а також дозволяють нагадати про єдиність подання раціонального числа у вигляді нескоротного дробу з цілим чисельником та натуральним знаменником.
Особливу групу складають вправи на повторення правил та поновлення обчислювальних навичок: вправи на порівняння і виконання арифметичних дій з наближеними значеннями чисел.
Особливу увагу приділяємо розв'язуванню вправ на доведення того, що дане число є ірраціональним на основі уявлення про те, що раціональне число можна подати у вигляді нескоротного дробу виду ![]() , де т — ціле, а п — натуральне число.
, де т — ціле, а п — натуральне число.
VII. Підсумки уроку
Яке з наведених тверджень правильне?
а) Число ![]() — раціональне; б) число
— раціональне; б) число ![]() — ірраціональне;
— ірраціональне;
в) число ![]() — дійсне; г) 0,6 = 0,(6).
— дійсне; г) 0,6 = 0,(6).
VIII. Домашнє завдання
- Вивчити теоретичний матеріал уроку (див. опорний конспект 10).
- Розв'язати вправи на застосування вивчених понять (змісту, аналогічного до змісту вправ класної роботи).
- На повторення: повторити означення квадратного кореня, арифметичного квадратного кореня, основну тотожність для квадратного кореня; розв'язати вправи на застосування названих понять.


про публікацію авторської розробки
Додати розробку
