Функція. Властивості функції

Функція. Властивості функції

Функцією называють таку залежність у від х, при якій кожному значенню х відповідає єдине значення у

х- аргумент, у- значення функції

1.Область визначення –усі значення аргументу (х)

Позначається D(y) або D(f)

2. Область значень – усі значення функції (y)

Позначається Е(y) або Е(f)

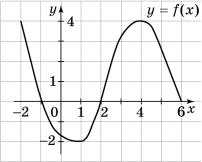
1) D(y)=[-2; 6]                      2) E(y)=[-2;4]

3.Нулі функції – значення аргументу (x), при яких значення функції (y)  дорівнює 0 (y=0)

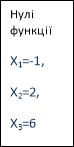
4.Перетин з  віссю ординат (Оу)  х=0  (0; -1,8)

5.Проміжки знакосталості – проміжки, на яких функція приймає додатні (y>0) або від’ємні (y<0) значення

1. y>0, якщо хЄ [-2;-1)U(2;6)
2. У<0, якщо хЄ (-1;2)

6. Інтервали монотнності функції

(Проміжки зростання, спадання функції)

1) Функція зростає на проміжку, якщо на цьому проміжку більшому значенню аргументу відповідає більше значення функції

(Якщо х₁<x₂, тоді  f(x₁)<f(x₂))

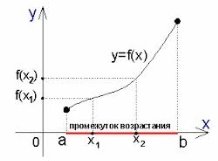
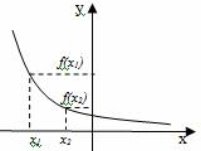
2) Функція спадає на проміжуку, якщо на цьому проміжку більшому значенню аргументу відповідає меньше значення функції

(Якщо х₁<x₂, тоді  f(x₁)>f(x₂))

1)Функція зростає, якщо хЄ[1; 4]

 2)Функція спадає, якщо  хЄ[-2; 1]U[4;6]

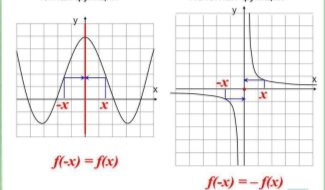
7. Парність, непарність  функції

1) Функцію y=f(x) называють парною, якщо для всіх  х з області визначення функції

f(-x)=f(x).

Графік парної функції симетричний відносно осі ординат

2) Функцію y=f(x) называют непарною, якщо для всіх  х з області визначення функції

f(-x)=-f(x).

Графік непарної функції симетричний відносно початку координат

        Парна функція              Непарна функція

8. Найбільше (y_max ) и найменше (y_min ) значення функції

y_min=-2                               y_max=4

Приклад

Властивості функції у=х⁴-2х²

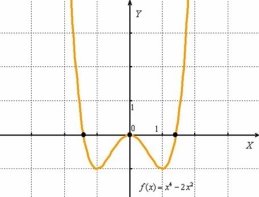
1. D(y)=(-∞; +∞) або  D(y)=R
2. E(y)=[-1;+∞)
3. Нулі функції: х₁= -1,5; х₂=0; х₃=1,5
4. Перетин з ОY:  (0;0)
5. Проміжки знакосталості:

а)  y>0, якщо хє(-∞; -1,5)U(1,5; +∞)

б)  у<0, якщо хє (-1,5; 0)U(0; +1,5)

6. а) Функція зростає, якщо

 хє[-1; 0]U[1; +∞)

7. б) Функція спадає, якщо

 хє[-∞; -1]U[0; 1]

8. Функція парна
9. у_min=-1