Функція , її властивості та графік.
Тема уроку. Функція ![]() , її властивості та графік.
, її властивості та графік.
Мета уроку: закріпити знання учнів про означення, вид графіка та алгоритм побудови графіка квадратичної функції. Дослідити властивості квадратичної функції та узагальнити ці спостереження, доповнивши ними знання про властивості квадратичної функції. Закріпити вміння розпізнавати квадратичну функцію серед інших елементарних функцій, знаходити координати вершини та напрям віток графіка квадратичної функції, виконувати побудову графіка квадратичної функції за вивченими алгоритмами. Виробити вміння застосовувати виконані на уроці спостереження для аналітичного дослідження властивостей квадратичної функції загального вигляду. Повторити загальні властивості функцій, а також схеми виконання основних видів геометричних перетворень графіків функцій.
Тип уроку: формування знань та вмінь.
Наочність та обладнання: опорний конспект № 16.
Хід уроку
I. Організаційний етап
Учитель перевіряє готовність учнів до уроку, налаштовує їх на роботу.
II. Перевірка домашнього завдання
Одним зі способів перевірки рівня засвоєння учнями знань та вмінь на попередньому уроці є математичний диктант (див. нижче).
Математичний диктант
- З графіка якої функції виду у = ах2 можна отримати паралель ним перенесенням графік функції:
1 варіант: у = -3х2 + 5х – 4; 2 варіант: у = -2х2 + 3х – 2?
- Укажіть координати вершини параболи:
1 варіант: у = -х2 + 6х – 8; 2 варіант: у = -х2 – 6х – 7.
- Чи перетинає вісь абсцис графік функції:
1 варіант: у = -х2 + х – 6; 2 варіант: у = -х2 – х + 6?
- Вгору чи вниз напрямлені вітки параболи:
1 варіант: у = ![]() х2 + 2х + 5; 2 варіант: у =
х2 + 2х + 5; 2 варіант: у = ![]() х2 + 3х + 6?
х2 + 3х + 6?
- Побудуйте ескіз графіка функції:
1 варіант: у = х2 – 6х + 8; 2 варіант: у = -х2 + 6х – 7.
Якщо при розв'язуванні вправ домашнього завдання учні мали значні труднощі, тоді доцільно провести перевірку домашнього завдання за зразком.
III. Формулювання мети і завдань уроку.
Мотивація навчальної діяльності учнів
Для усвідомлення учнями необхідності вивчення матеріалу, запропонованого на поточний урок, учитель може провести роботу, що передбачає розв'язання учнями завдань на виконання таких розумових дій, як порівняння (знаходження спільного та відмінного), а також узагальнення та формулювання гіпотези. Наприклад, учитель пропонує учням такі завдання.
Завдання 1
Розгляньте графіки кількох квадратичних функцій, вітки яких напрямлені вгору, та визначте за цими графіками проміжки зростання кожної із функцій; порівняйте отримані результати. Що ви помітили? Тепер визначте проміжки спадання цих самих функцій; порівняйте отримані результати. Що ви помітили? Сформулюйте припущення.
Завдання 2
Розгляньте графіки кількох квадратичних функцій, вітки яких напрямлені вгору, та визначте за цими графіками область визначення кожної із функцій. Порівняйте результати. Що ви помітили? Сформулюйте припущення.
Після проведеної роботи учні мають сформулювати питання (проблему): чи не можна узагальнити у вигляді математичних тверджень зв'язок між коефіцієнтами в рівнянні квадратичної функції та її властивостями? Пошук відповіді на поставлене запитання і становить основну дидактичну мету уроку.
IV. Актуалізація опорних знань та вмінь учнів
Усні вправи
- Укажіть координати вершини, напрям віток та рівняння вісі симетрії параболи:
1) у = х2 – 1; 2) у = -2х2 + 5; 3) у = (х – 2)2; 4) у = -3(х + 1)2 – 4.
- Визначте координати точки перетину з віссю ординат параболи:
1) у = 2х2 – 5х + 2; 2) у = -х2 + 3; 3) у = 2х – 3х2.
-
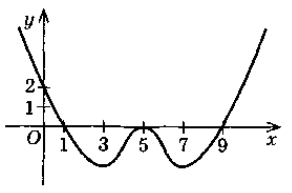
На рисунку зображено графік функції f. Визначте:
- при яких х функція зростає; спадає;
- при яких х функція набуває значень, що дорівнюють нулю, більші нуля, менші нуля;
- при яких значеннях х на відрізку [1;7] функція набуває найменшого значення, найбільшого значення.
V. Формування знань
План вивчення нового матеріалу
- Область визначення квадратичної функції; область значень квадратичної функції.
- Проміжки зростання та проміжки спадання функції y = ax2 + bx + c.
- Проміжки знакосталості функції y = ax2 + bx + c.
Опорний конспект №16
|
|
Властивості квадратичної функції
(функції виду у = ax2 + bx + c, а |
|
|
|
|
а > 0 |
а < 0 |
|
|
|
1. D(y) = R 2. Е(у) = [у0; +∞) |
1. D(y) = R 2. Е(у) = (-∞; y0] |
|
|
|
(у0 — ордината вершини параболи) |
|
|
|
|
3. а) Функція зростає, якщо
х б) Функція спадає, якщо
х |
3. а) Функція зростає, якщо
х б) Функція спадає, якщо
х |
|
|
|
(х0 — абсциса вершини параболи) |
|
|
|
|
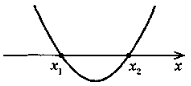
4. а) Якщо D > 0, то
у > 0 при х
у < 0 при x
|
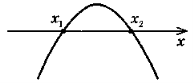
4. а) Якщо D > 0, то
у > 0 при х
у < 0 при x
|
|
|
|
(х1, х2 – нулі функції) |
|
|
|
|
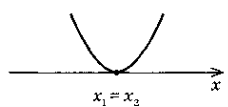
б) Якщо D = 0, то у > 0
при х
|
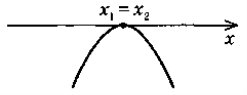
б) Якщо D = 0, то у < 0
при х
|
|
|
|
в) Якщо D < 0, то у > 0 при x
|
в) Якщо D < 0, то у < 0 при х
|
|
|
|
|
|
|
Методичний коментар
Узагальнення відомостей про основні властивості функції у = ах2 + bх + с, а ![]() 0, відбувається як результат спостережень, які учні проводять на даному уроці та проводили на попередньому уроці при роботі з визначенням властивостей квадратичних функцій за побудованими графіками. Головна мета цієї роботи (і на цьому слід акцентувати увагу учнів) — показати, що властивості квадратичної функції (як і будь-якої функції) закладені в самому рівнянні функції, а отже, можуть бути виявлені аналітично (визначенням знака коефіцієнта а, координат вершин параболи, а також знака дискримінанта та коренями квадратного тричлена ах2 + bх + с); графік функції лише наочно демонструє ці властивості.
0, відбувається як результат спостережень, які учні проводять на даному уроці та проводили на попередньому уроці при роботі з визначенням властивостей квадратичних функцій за побудованими графіками. Головна мета цієї роботи (і на цьому слід акцентувати увагу учнів) — показати, що властивості квадратичної функції (як і будь-якої функції) закладені в самому рівнянні функції, а отже, можуть бути виявлені аналітично (визначенням знака коефіцієнта а, координат вершин параболи, а також знака дискримінанта та коренями квадратного тричлена ах2 + bх + с); графік функції лише наочно демонструє ці властивості.
VI. Формування вмінь
Усні вправи
- Графіком деякої квадратичної функції є парабола, вітки якої напрямлені вгору; координати вершини (-3; -2); точки перетину з віссю абсцис мають координати -4 і -2. За цими даними назвіть:
- область визначення цієї функції;
- область значень цієї функції; її найменше значення; чи існує найбільше значення функції;
- проміжок, на якому функція зростає:
- проміжок, на якому вона спадає:
- проміжок, на якому функція набуває додатних значень:
- проміжок, на якому функція від'ємна.
Письмові вправи
Приблизний зміст вправ може бути таким:
- не виконуючи побудови графіка функції у = ах2 + bх + с, дослідити її властивості;
- побудувати графік функції у = ах2 + bх + с та за графіком дослідити її властивості;
- розв'язати (графічно та аналітично) рівняння виду f(x) = ах2 + bх + с (f(x) — яка-небудь з елементарних функцій змінної х) та за допомогою графіка функції у = ах2 + bх + с розв'язати нерівності ах2 + bx + c > 0, ах2 + bх + с < 0;
- на повторення: вправи на геометричні перетворення графіків функцій.
Методичний коментар
Усні вправи сприяють закріпленню учнями узагальнених властивостей квадратичної функції та схем дій при аналітичному дослідженні її властивостей.
При розв'язуванні письмових вправ на уроці слід вимагати від учнів чіткого відтворення записаних узагальнених властивостей та дій відповідно до них.
(Наприклад, учні мають відтворювати такі міркування: щоб знайти область значень квадратичної функції, визначаємо знак старшого коефіцієнта та ординату вершини параболи за формулою; оскільки старший коефіцієнт додатний, то область значень функції — це проміжок [у0; + °°) і т. д.)
VII. Підсумки уроку
Контрольні запитання
- Яким числом може бути коефіцієнт а в рівнянні у = ах2 + 6х + с, якщо ця функція спадає на проміжку:
1) х ![]()
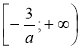 ; 2) х
; 2) х ![]()
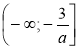 ?
?
-
Куди напрямлені вітки параболи, що є графіком функції у = ах2 + bх + с, якщо функція набуває:
- найбільшого значення, яке дорівнює 3;
- найменшого значення 3?
Чи є в цієї функції проміжки, на яких вона додатна? від'ємна?
VIII. Домашнє завдання
- Повторити означення квадратичної функції, вид її графіка та алгоритм побудови графіка функції у = ах2 + bх + с.
- Вивчити алгоритм аналітичного дослідження квадратичної функції.
- Виконати самостійну роботу № 5 [8] за двома варіантами.
- Повторити: означення нерівності з однією змінною та супутні поняття; схеми розв'язування лінійних нерівностей з однією змінною.


про публікацію авторської розробки
Додати розробку