Квадратна нерівність. Розв'язування квадратних нерівностей.

Тема уроку. Квадратна нерівність. Розв'язування квадратних нерівно­стей.

Мета уроку: сформувати знання учнів про зміст поняття «квадратна нерівність», домогтися розуміння та засвоєння учнями схеми розв'язування квадратних нерівностей із використанням побудови графіка квадратичної функції. Сформувати пер­винні вміння вирізняти квадратні нерівності серед інших нерівностей з однією змінною; за готовими графіками квадратичної функції знаходити розв'язки відповідних квадратних нерівностей, а також виконувати послідовні дії відповідно до вивченої схеми для відшукання розв'язків квадратних нерівностей різного виду.

Тип уроку: формування знань, вироблення первинних умінь.

Наочність та обладнання: опорний конспект № 17.

Хід уроку

I. Організаційний етап

Учитель перевіряє готовність учнів до уроку, налаштовує їх на роботу.

II. Перевірка домашнього завдання

Учитель збирає зошити для перевірки та оцінювання якості виконання домашньої самостійної роботи; учням можна роздати правильні розв'язання для самостійного аналізу помилок (якщо такі є).

ІІІ. Формулювання мети і завдань уроку.

Мотивація навчальної діяльності учнів

Учитель повідомляє учнів про те, що крім чисто наукового інтересу квадратична функція та побудова її графіка мають своє практичне застосування: побудова графіка квадратичної функції є одним із засобів розв'язування нерівностей відповідного виду. Такі нерівності мають назву квадратних нерівностей (або нерівно­стей другого степеня). Мета даного уроку — вивчення означення квадратних нерівностей, схеми їх розв'язування, а також форму­вання вмінь застосовувати вивчене означення та схему для того, щоб відрізняти квадратні нерівності від інших нерівностей з од­нією змінною та знаходити розв'язки квадратних нерівностей.

IV. Актуалізація опорних знань та вмінь учнів

Усні вправи

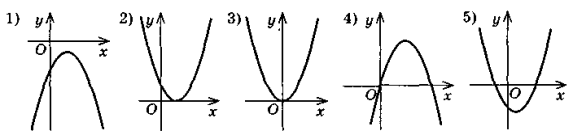
1. Серед наведених рівнянь укажіть рівняння, що задають ква­дратичну функцію:

1) у = 2х² + х – 1;   2) у² = х + 1;  3) у² = х² – 1;

4) у = -х – х²;   5) у² = х²;   6) у = -х².

Для вказаних функцій назвіть коефіцієнти квадратного три­члена (у формулі у = ах² + bх + с).

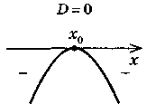
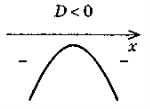
2. Дано умови:

а) а > 0; D > 0; c < 0;   б) а > 0; D = 0; c > 0;  

в) а < 0; D < 0; c < 0;   г) а < 0; D > 0; c = 0;

д) а > 0; с = 0; D = 0.

Із запропонованих рисунків графіків функції у = ах² + bх + с оберіть той, що задовольняє кожну з даних умов:

3. Знайдіть нулі функції (якщо вони існують):
   1) у = 2х – 3;  2) у =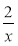 ; 3) у = 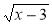;  4) у = х² – 3х + 2.

V. Формування знань

План вивчення нового матеріалу

1. Означення квадратної нерівності. Приклади квадратних нерів­ностей з різними коефіцієнтами.
2. Схема розв'язування квадратних нерівностей за допомогою по­будови графіка відповідної квадратичної функції.
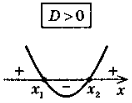
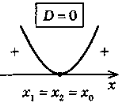
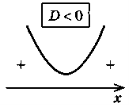
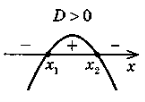
3. Різні способи розташування графіка квадратичної функції y = ax² + bx + c відносно осі Ох залежно від знака старшого коефіцієнта та знака дискримінанта квадратного тричлена ах² + bх + с.

Опорний конспект №17

Методичний коментар

Вивчення питання про розв'язування квадратних нерівно­стей розпочинається з формування знань про зміст означення квадратних нерівностей. Слід наголосити на тому, що так само, як і квадратний тричлен, квадратна нерівність може мати «ско­рочений» вигляд (див. приклади, наведені в опорному конспекті № 17). Цей момент є принциповим, бо, як свідчить досвід, досить велика кількість учнів, розв'язуючи такі нерівності, допускають помилку: нерівності виду ах² + с > 0 замінюють на нерівносильну нерівність     х > .

Схема розв'язування квадратних нерівностей опановується учнями в 9 класі, тому основана на використанні графіка відпо­відної квадратичної функції й передбачає знаходження проміжків знакосталості цієї функції за ескізом графіка.

На етапі формування вмінь розв'язувати квадратні нерівності за вивченою схемою слід вимагати від учнів чіткого виконання наступних дій: звести нерівність до виду квадратної; відшукати дійсні корені квадратного тричлена (якщо вони існують) та побу­дувати ескіз графіка квадратичної функції; записати проміжок, на якому функція набуває знака, що відповідає даній квадратичній нерівності (з урахуванням строгості знака нерівності).

Попередженням можливих труднощів учнів при розв'язу­ванні квадратних нерівностей є робота з певного узагальнення випадків взаємного розташування графіка квадратичної функції відносно координатної осі абсцис залежно від знака старшого коефіцієнта та знака дискримінанта відповідного квадратного тричлена.

VI. Формування вмінь

Усні вправи

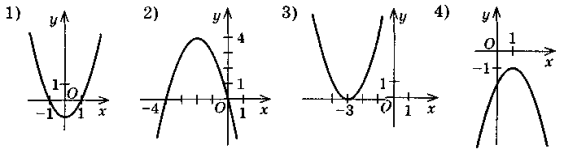
1. Дано нерівності:

а) ах² + bx + c > 0;    б) ах² + bx + c < 0;

в) ах² + bх + с > 0;    г) ах² + bx + c < 0.

Знайдіть розв'язок кожної з даних нерівностей за графіком функції

у = ах² + bх + с, зображеним на рисунку:

2. Чи є число: 0; 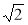; -3 — розв'язком нерівності:

1) 2х + 3 < 0;   2) х² ≤ 0;  3) х² > 2?

3. Яка з нерівностей не є квадратною?

1) х² – 44 > 0;   2) х² + 3 < 0;  3) х² + 3х³ > 0;  4) -х² – 5 ≤ 0.

Письмові вправи

Зміст вправ, запропонованих до розв'язування на уроці, може бути таким:

1. знайти розв'язки квадратної нерівності за готовим графіком відповідної квадратичної функції;
2. розв'язати за вивченою схемою квадратні нерівності;
3. розв'язати нерівності другого степеня, що зводяться до ква­дратних рівносильними перетвореннями;
4. на повторення: установити властивості функції за даним гра­фіком цієї функції.

Методичний коментар

Вправи до уроку спрямовані на засвоєння учнями сформу­льованого означення квадратної нерівності й вироблення вміння вирізняти квадратні нерівності серед інших нерівностей з однією змінною, спираючись на вивчене означення, розв'язання запропонованих вище вправ також сприятиме засвоєнню учнями розгля­нутої схеми розв'язування квадратних нерівностей і виробленню вмінь її застосовувати для відшукання розв'язків як квадратних нерівностей, так і нерівностей, що зводяться до квадратних шля­хом рівносильних перетворень. Розв'язання вправ на повторен­ня — на застосування властивостей функції — сприятиме підго­товці учнів до наступної контрольної роботи.

VII. Підсумки уроку

Контрольні запитання

1. Визначте знак коефіцієнта а, коефіцієнта с, дискримінанта D за графіком функції у = ах² + bх + с, зображеним на рисунку:

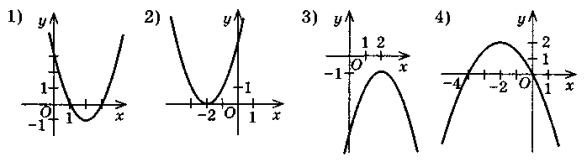
2. Яка квадратна нерівність має розв'язком проміжок (див. ри­сунки вище):

1) x [1; 3];     2) x R; 

3) х (-∞; -4) (0; +∞);   4) розв'язків немає.

VIII. Домашнє завдання

1. Вивчити означення квадратної нерівності, схему її розв'язу­вання (див. опорний конспект № 17).
2. Розв'язати вправи на застосування вивченого означення та схе­ми, аналогічні за змістом та рівнем складності розв'язаним на уроці.
3. Повторити: як знайти область визначення функції, заданої рів­нянням виду y = f(x); означення поняття системи нерівностей, а також зміст поняття «дискримінант квадратного рівняння».