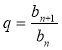Геометрична прогресія.

Тема уроку. Геометрична прогресія.

Мета уроку: домогтися засвоєння учнями: означення геометричної про­гресії, відповідної термінології (знаменник геометричної прогресії), її рекурентної формули та основних властивос­тей геометричної прогресії (включаючи характеристичну властивість). Виробити вміння: відтворювати зміст вивче­них понять, а також використовувати їх для розв'язування задач, що передбачають виділення геометричної прогресії серед інших числових послідовностей, використання рекурентної формули геометричної прогресії, а також використання її властивостей.

Тип уроку: засвоєння знань, вироблення вмінь.

Наочність та обладнання: опорний конспект № 33.

Хід уроку

I. Організаційний етап

Учитель перевіряє готовність учнів до уроку, налаштовує їх на роботу.

II. Перевірка домашнього завдання

Учитель збирає зошити учнів на перевірку.

III. Формулювання мети і завдань уроку.
Мотивація навчальної діяльності учнів

Для усвідомлення учнями необхідності виділення та подальшо­го вивчення властивостей геометричної прогресії, винесених у тему уроку, можна запропонувати їм виконати вправу на порівняння або логічну вправу на виключення зайвого (наприклад, серед за­пропонованих послідовностей кілька є такими, що надалі можуть бути визначені як геометричні прогресії, а одна з них такою не є; або навпаки, серед кількох відомих учням арифметичних прогре­сій дати одну геометричну та, виділивши її як «зайву», проаналі­зувати відмінність цієї послідовності від геометричної прогресії).

Після виконання таких вправ учні усвідомлюють, що серед не­скінченної кількості різних за видами числових послідовностей, крім виділених на попередніх уроках видів, можна виділити інші види. Від них відокремлюються послідовності, у яких кожний на­ступний член, на відміну від членів арифметичної прогресії, до­рівнює попередньому члену, помноженому на те саме число. Після такого умовиводу формулюється основна дидактична мета уроку: вивчити означення, дати назву та дослідити властивості таких по­слідовностей та їх застосування.

IV. Актуалізація опорних знань та вмінь учнів

Усні вправи

1. Знайдіть:

1. значення функції, заданої формулою у = 3х⁵ при х = 0; 1; -1;
2. при якому значенні аргументу значення функції у = х² – 3х + 2 дорівнює 0; 2; -2;
3. при яких значеннях аргументу значення функції у = 1-2х додатні; від'ємні.

2. Спростіть вираз:

1) 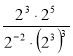;  2) ;   3) 3^п-1 ∙ 3^п.

3. Розв'яжіть рівняння:

1) b² = 3;   2) x³ = 27;   3) q⁶ = .

4. Послідовність (х_п) задана формулою х_n = 81 ∙ 3^1-n. Знайдіть:
   1) х₁, х₂, х₃;   2) відношення , , .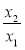

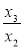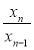V. Формування знань

План вивчення нового матеріалу

1. Означення геометричної прогресії. Знаменник геометричної прогресії.
2. Рекурентна формула геометричної прогресії.
3. Властивості геометричної прогресії:

1) характеристична властивість;

2) добутки двох членів скінченної геометричної прогресії, рівно від-далених від її кінців.

Опорний конспект № 33

Методичний коментар

Формування знань учнів на даному уроці проводиться за тією самою схемою, що і на уроці, коли вивчалися означення та основні властивості арифметичної прогресії. Вивчення матеріалу уроку по­чинається з формулювання означення геометричної прогресії (учні підготовлені до його сприйняття на попередньому етапі уроку), у якому слід звернути увагу учнів на словосполучення «починаючи з другого», а також на те, що число, на яке помножують кожний член, починаючи з другого, є сталим для даної геометричної про­гресії, при цьому воно може бути яким завгодно (додатним або від'ємним, цілим або дробовим; воно тільки не може, на відмі­ну від різниці арифметичної прогресії, дорівнювати 0; це бажано проілюструвати великою кількістю прикладів). Після цього фор­мулюється уявлення про зміст поняття «знаменник геометричної прогресії» та записується відповідна формула. Далі традиційно записується рекурентна формула геометричної прогресії, яка на­пряму випливає з означення геометричної прогресії.

Для розв'язування багатьох прикладних задач важливими є властивості геометричної прогресії, зокрема характеристична властивість (хоча програма з математики не дає її серед обов'язкових знань у цій темі). Також не обов'язковою, проте цікавою для за­стосування є властивість членів скінченної геометричної прогре­сії, рівновіддалених від її крайніх членів. Тому, якщо дозволяють особливості класу, можна запропонувати всі названі властивості геометричної прогресії розглянути як додатковий матеріал (див. опорний конспект № 33).

VI. Формування вмінь

Усні вправи

1. За означенням перевірте, чи є геометричною прогресією по­слідовність:

а) степенів числа 2 з цілими додатними показниками — 1; 2; 4; 8; 16; ...;

б) кубів натуральних чисел — 1; 8; 27; 64; ... .

2. Укажіть перший член та знайдіть знаменник геометричної про­гресії:

1) 1; -5; 25; ...;  2) -6; -6; -6; ...;  3) 9; 3; 1; ...;

4) 7; ; ; ...;  5) -3; 3; -3; ... .

3. Знайдіть другий і третій члени геометричної прогресії (b_п), якщо:

1) b₁ = 3, q = 2;  2) b₁ = 5, q = -1.

Письмові вправи

Для реалізації дидактичної мети уроку слід розв'язати вправи такого змісту:

1. серед запропонованих послідовностей вибрати геометричні про­гресії;
2. указати n-й член та знаменник геометричної прогресії, заданої переліком її перших членів;
3. за рекурентною формулою знайти кілька перших членів гео­метричної прогресії;
4. вправи на використання властивостей геометричної прогресії;
5. на повторення: вправи на розв'язування степеневих рівнянь.

Методичний коментар

При розв'язуванні вправ, крім закріплення термінології та формул, що виражають властивості геометричної прогресії, про­водиться відпрацювання схем дій у таких стандартних ситуаціях: перевірити, чи є задана послідовність геометричною прогресією (за означенням, або за характеристичною властивістю, або за те­оремою, залежно від умови); знайти знаменник геометричної про­гресії, якщо відомі два сусідні її члени; знайти член, наступний за даним членом геометричної прогресії.

VII. Підсумки уроку

Контрольні запитання

1. Яка послідовність називається геометричною прогресією? На­ведіть приклади.
2. Чому дорівнює відношення двох сусідніх членів геометричної прогресії, починаючи з другого?
3. Як задати геометричну прогресію?

VIII. Домашнє завдання

1. Вивчити означення та властивості геометричної прогресії, роз­глянуті на уроці (див. опорний конспект № 33).
2. Розв'язати вправи, аналогічні за змістом та рівнем складності виконаним на уроці.
3. Повторити схему розв'язування задач складанням математич­ної моделі.