Геометричне місце точок. Метод геометричних місць

Тема. Геометричне місце точок. Метод геометричних місць

Мета: учні мають засвоїти поняття «геометричне місце точок» (ГМТ) і той факт, що коло і круг — це приклади певних гео­метричних місць точок; вивчити в підручнику розв'язання прикладів на знаходження ГМТ і, таким чином, ознайоми­тися із способом розв'язання задач цього типу. Виробити вміння відтворювати вивчені твердження про ГМТ, а також використовувати їх при виконанні найпростіших побудов для розв'язання задач на знаходження (побудову) де­яких ГМТ.

Тип уроку: засвоєння нових знань, вироблення вмінь

Обладнання: набір демонстраційного креслярського приладдя.

Хід уроку

І. Організаційний етап

II. Перевірка домашнього завдання    

Як і на попередньому уроці, можна зібрати аркуші з викона­ним домашнім завданням і за попередньо зробленими на дошці рисунками прокоментувати розв'язання всіх задач.

III. Формулювання мети і завдань уроку    

Методичний   коментар

Оскільки основне поняття уроку (ГМТ) є абсолютно новим для учнів і, як свідчить досвід, не є простим для багатьох учнів, важливо створити позитивну мотивацію навчальної діяльності учнів. Для цього можна запропонувати їм для розв'язання задачу-жарт:

Козу прив'язали до кілка мотузкою, довжина якої 5 м. Коза паслася весь день, поки не з'їла всю траву, до якої могла дістатись. Яку форму матиме вищипана козою ділянка, якщо мотузка не накручувалася на кілок.

Зрозуміло, що більшість учнів знайдуть правильну відповідь на запитання (круг радіуса 5 м), але вчителю слід зосередити увагу учнів на геометричному змісті цієї задачі, а саме: запропонувати учням подати умову цієї задачі мовою математики (створити математичну модель задачі). Успішно виконавши цю роботу, учні усвідомлять той факт, що деякі геометричні фігури відрізняються від інших тим, що всі їх точки мають принаймні одну спільну властивість (наприклад, усі вони рівновіддалені від якої-небудь точки або прямої, тощо).

Цей висновок і має бути тією рушійною силою, що підштов­хне учнів до розуміння необхідності більш детального вивчення властивостей таких фігур для подальшого використання цих властивостей при розв'язуванні задач (це фактично і є основна дидактична мета уроків 44—45).

IV. Актуалізація опорних знань і вмінь учнів   

Запитання   до   класу

1. Відомо, що АВ = АС. Що можна сказати про положення точки А по відношенню до точок В і С?
2. Відомо, що АВ = АС = АМ. Що можна сказати про по­ложення точки А по відношенню до точок В, С і М?
3. У трикутнику ABC сторони АВ і ВС рівні, ВМ — медіана. Точка К лежить на медіані ВМ. Що спільного у точок В, М і К по відношенню до точок А і В?
4. Відомо, що МА є відстанню від точки М до прямої АВ. Чи може кут МАВ дорівнювати  70°,  120°,   90°?

V. Засвоєння нових знань    

План вивчення нового матеріалу

1. Означення ГМТ.
2. Приклади ГМТ, відомих учням.
3. Задача про пошук ГМТ, рівновіддалених від двох даних точок.
4. Задача про пошук ГМТ, рівновіддалених від сторін кута.

Методичний   коментар

При підготовці до уроку з теми ГМТ вчитель має зважати на те, що цей матеріал традиційно є досить складним для учнів, отже, важливо врахувати рівень підготовки учнів до його сприйняття. Тому на етапі засвоєння знань учитель на свій розсуд або проводить бесіду, спираючись при цьому на спостереження, здійснені під час пошуку відповідей на за­питання п. 4 уроку, або організує самостійну роботу учнів з підручником (§ 18) з метою виявлення учнями нових понять і складання загального плану розв'язування задач, подібних до задач 1 та 2 (див. с. 141, 142 підручника).

У будь-якому разі після опрацювання навчального матеріалу уроку кожен учень має усвідомити, що розв'язування задач про пошук ГМТ передбачає:

• пошук усіх точок, які задовольняють умові задачі;
• доведення того факту, що всі інші точки площини не є розв'язками задачі.

Також важливо, щоб учні зрозуміли, що пошук нових, неві­домих їм раніше ГМТ можна здійснювати поступово: спочатку серед відомих ГМТ виокремити ті ГМТ, що задовольняють умові задачі частково, а потім уже серед точок цього ГМТ відшукати ті, що задовольняють умові задачі повністю.

VI. Первинне усвідомлення матеріалу    

Графічні   вправи

1. З підручника виконати вправи № 534 — 536; перед ви­конанням побудов прокоментувати своє рішення, або запропонувати ці завдання для самостійного виконання з наступною перевіркою і корекцією результатів.
2. Додатково: побудуйте точку, рівновіддалену від сторін даного трикутника. Чим є ця точка для даного трикут­ника?
3. А також пропонуємо учням розв'язати задачі № 537 і 538.

Методичний   коментар

При розв'язуванні задач № 537 і 538 учні мають дотриму­ватися вимог до розв'язування задач про пошук ГМТ (див. п. 5) і при виконанні самих побудов застосовувати вивчені алгоритми виконання геометричних побудов.

VII. Підсумки уроку    

Запитання до класу Як можна назвати геометричне місце точок, зображене на рис. 138?

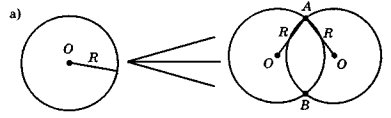
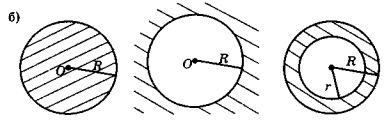
Рис. 138

VІІІ. Домашнє завдання

1. § 18 — вивчити означення і приклади найпростіших ГМТ.
2. Розв'язати задачі.

1) Чи можна вважати круг радіуса 5 см геометричним місцем точок, що віддалені від центра цього круга на відстань, яка:

а) дорівнює 5 см;  б) не більше 5 см;

в) не менше 5 см;  г) не більша 4 см?

2) Точки А, В і С не лежать на одній прямій. Побудуйте точку, рівновіддалену від точок А, В і С.

3) Побудуйте точку, рівновіддалену від сторін даного кута, що лежить на відстані а від його вершини.