Розробка уроку на тему "Задачі на побудову"

Тема. Задачі на побудову

Мета: закріпити знання схеми розв'язання задач на побудову; повторити і систематизувати вивчений матеріал з теми «Коло. Геометричні побудови». Повторити, систематизу­вати і узагальнити вміння учнів використовувати набуті знання для розв'язання задач на обчислення, доведення і побудову.

Тип уроку: повторення, узагальнення та систематизація знань і вмінь.

Обладнання: набір демонстраційного креслярського приладдя, таблиці № 18 -23.

Хід уроку

І. Організаційний етап  

ІІ. Перевірка домашнього завдання   

Оскільки розв'язання задачі № 619 (3, 4) було проаналізо­вано в класі, ретельно перевіряємо розв'язання задачі № 620.

Для більшої продуктивності роботи з перевірки домашнього завдання роздаємо всім учням копії або повного розв'язання задач, і вони коментують кожний його етап, або неповного розв'язання (наприклад, тільки рисунки), і учні роблять до них письмові доповнення. В такому разі вчитель зможе перевірити роботу кожного учня, зібравши заповненні учнями копії.

III. Формулювання мети і завдань уроку     

Саме те, що урок в темі є заключним, створює певну моти­вацію діяльності учнів і визначає головну мету уроку: після повторення, систематизування і узагальнення знань учнів про властивості кола, його елементів і пов'язаних з колом ситуацій, повторити, узагальнити і систематизувати способи дій, які ма­ють застосовувати учні при розв'язуванні задач на обчислення, доведення і побудову.

IV. Систематизація знань учнів

Цей етап уроку можна провести у формі теоретичної само­стійної роботи учнів.

Самостійна   робота   №   9

Варіант 1

1. Яку лінію утворюють усі точки, що віддалені від точки О на 2 см?
2. У рівносторонньому трикутнику проведено дві медіани. Чи можна вважати точку їх перетину центром кола, вписаного в цей трикутник?
3. У трикутник ABC вписано коло з центром у точці О. Відстань від точки О до прямої ВС дорівнює 7 см. Чому дорівнює відстань від точки О до прямої АС?
4. Дано нерівносторонній трикутник. Визначте, чи є коло вписаним у трикутник, чи описаним навколо нього, якщо центр кола рівновіддалений від усіх вершин цього трикутника.
5. З точки, що лежить на колі, проведено три відрізки, один із яких проходить через центр кола і з'єднує дві точки кола. Довжини цих відрізків дорівнюють 3 см, 4 см, 8 см. Знайдіть довжину хорди

Варіант 2

1. Яку лінію утворюють усі точки, що віддалені від точки О на 5 см?
2. У рівносторонньому трикутнику проведено дві висоти. Чи можна вважати точку їх перетину центром кола, описаного навколо цього трикутника?
3. Навколо трикутника ABC описано коло з центром у точці О. Відстань від точки О до вершини В становить 6 см   Чому дорівнює відстань від точки О до точки А?
4. Дано нерівносторонній трикутник і коло. Визначте, чи коло вписано в трикутник, чи описано навколо нього, якщо центр кола рівновіддалений від усіх сторін цього трикутника.
5. З точки, що лежить на колі, проведено три відрізки, один із яких з'єднує дану точку з центром кола і є най­меншим відрізком. Довжини цих відрізків дорівнюють 3 см, 4 см, 8 см. Знайдіть довжину хорди

V. Систематизація вмінь учнів   

А. Практичні вправи з реалізації вмінь у стандартних ситуа­ціях.

Усні   вправи

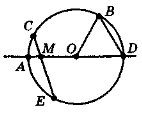
1. Назвіть елементи кола: радіуси, центр, хорди, діаметр (рис. 142). Знайдіть:

а) радіус, якщо  AD = 7 см;

б) кути OBD і ODB, якщо кут BOD дорівнює  80°;

в) кути трикутника OBD, якщо зовнішній кут при вер­шині О трикутника OBD дорівнює  140°;

г) кут АМС, якщо  СМ = МЕ.

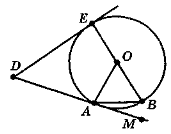
2. DE і DA — дотичні до кола (рис.  143). Знайдіть:

а) кути трикутника ОАВ, якщо кут ВАМ дорівнює 20°;

б) DE, якщо DA = 10 см;

в) кут EDA, якщо кут ЕОА дорівнює 120°;

г) ЕО, якщо  DO = 10 см і кут ЕОА дорівнює 120°.

Б.   Практичні вправи з реалізації вмінь у нестандартних ситуаціях.

На даному етапі уроку учні мають перейти до розв'язання більш складних задач за такою тематикою:

1) означення кола та його елементів, дотичної до кола та їх властивості;

2) уписані кути та їх властивості;

3) геометричні побудови, ГМТ; уписані та описані трикут­ники;

4) задачі на побудову.

Письмові   вправи

1. Дві взаємно перпендикулярні хорди кола, перетинаючись, поділяються на відрізки довжиною 5 см і 13 см. Знайдіть радіус кола, яке дотикається до хорд і має з колом спільний центр (рис. 144).

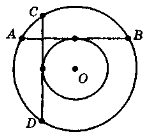
Рис. 144

2. Побудуйте рівнобедрений трикутник за основою і бісек­трисою, проведеною до основи.
3. Бічна сторона рівнобедреного трикутника ділиться точкою дотику вписаного кола у відношенні 3:2, якщо раху­вати від вершини (що лежить проти основи). Знайдіть периметр трикутника, якщо його основа на 1 см менша від бічної сторони.
4. Знайдіть градусну міру вписаного кута, якщо вона в сумі з градусною мірою відповідного центрального кута ста­новить  180°.

VI. Підсумки уроку    

На цьому етапі уроку бажано, щоб учні самі оцінили рівень своїх попередніх досягнень і виокремили питання, над якими їм слід попрацювати самостійно, щоб якнайкраще підготуватися до тематичної контрольної роботи.

VII. Домашнє завдання    

Домашня   контрольна   робота

1. Через точку А кола з центром у точці О проведено хор­ду АВ і діаметр АС. Знайдіть кут ВАС, якщо кут ВОС дорівнює  70°.
2. Прямі СА і СВ — дотичні до кола з центром у точці О. Доведіть, що ОС — бісектриса кута АОВ.
3. Два кола з радіусами 32 см і 12 см дотикаються. Знай­діть відстань між центрами цих кіл. Скільки розв'язків має ця задача?
4. Точка дотику вписаного кола ділить сторону рівностороннього трикутника на два відрізки, один із яких на 15 см менший від периметра трикутника. Знайдіть сто­рону трикутника.
5. Побудуйте рівнобедрений трикутник за бісектрисою, проведеною до основи і радіусом описаного кола.
6. Знайдіть кути рівнобедреного трикутника, якщо його основу видно з центра описаного кола під кутом 100° (рис. 145).

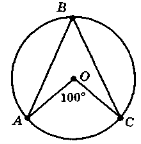
Рис. 145