Геометричні фігури та їх властивості
Урок №________ Дата_________
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() Тема уроку. Геометричні фігури. Точка. Пряма. Промінь. Властивості точок і прямих.
Тема уроку. Геометричні фігури. Точка. Пряма. Промінь. Властивості точок і прямих.
Мета уроку:
навчальна: ознайомити учнів із новим для них предметом геометрією, із
поняттям найпростіших фігур у геометрії, домагатися від учнів свідомого засвоєння термінології, що описує взаємне розташування точок та прямих на площині, формулювання основних властивостей розташування точок та прямих; виробити первинні вміння позначати точки та прямі на рисунку, описувати ситуацію, що зображена на рисунку та, навпаки, за описом ситуації виконувати відповідні рисунки, користуючись найпростішим креслярським приладдям, дати означення променя .
розвиваюча: активізувати пізнавальну діяльність учнів
виховна: виховувати акуратність, працьовитість, інтерес до вивчення геометрії, до історії розвитку науки.
Тип уроку: урок засвоєння нових знань.
Хід уроку
І. Організація класу. Психологічне налаштування.
Розповідь учителя
Перші геометричні уявлення в людей виникли ще за давніх-давен, коли людина виготовляла й використовувала у своїх цілях найпростіші знаряддя праці — кремнієві пластинки, що мали форму трикутника, ромба або трапеції. Вони використовувалися як рубило, шкребок, ніж і т.п. Але більш глибокого розвитку геометричні уявлення досягли із зародженням землеробства, будівництва, гончарної і ткацької справи. Залишки домашнього начиння, що дійшли до нас, переконливо свідчать про те, що в первісних людей тієї епохи «почуття» геометрії було досить добре розвинене. Вдивляючись в орнаменти, якими вони прикрашали свої вироби, ми спостерігаємо складні поєднання кіл, квадратів, прямокутних спіралей, що повторюються, рівність, подібність, симетрію різних фігур.
Згодом розв'язання багатьох практичних задач вимагало усе більшого обсягу глибоких і різнобічних знань.
Геометрія — слово грецького походження. Воно означає землемірство.
Першими «землемірами» були стародавні єгиптяни. Сільське господарство могло розвиватись лише біля річки Ніл. Щороку Ніл розливався, приносячи на землі які були залиті водою, плодючий мул. Кожен селянин мав наділ землі певної площі, однак розливи ріки не дозволяли раз і назавжди визначити межі кожного наділу, тому після чергового розливу доводилось визначати земельну ділянку заново. Це виконували землеміри — люди, що за допомогою шнура відміряли кожному селянину ділянку з площею, яка була йому приписана. Стародавні єгиптяни не знали циркуля, його винайшли греки. Однак це їм особливо не перешкоджало. Так, прямий кут вони будували мотузкою, що має довжину 12 мір. За допомогою цієї мотузки можна побудувати трикутник зі сторонами 3, 4 і 5 мір. Такий трикутник за теоремою Піфагора є прямокутним. Тому прямокутний трикутник також називають єгипетським.
У Стародавній Греції, починаючи з 7 століття до н. е., з часів Фалеса Мілетського, починається новий етап розвитку геометрії. Вона набуває характерного для неї абстрактного напряму, у ній виникає доведення. Так виникла геометрія в Єгипті, звідти вона потрапила до Греції.
Свій розвиток геометрія здобула у працях Фалеса, Піфагора, ІІлатона, Архімеда й інших давньогрецьких математиків, що жили в VI—III ст. до н. ери. Першу, що дійшла до нас, книгу з геометрії — «Начала», за якою протягом двох тисячоліть люди вивчали геометрію, написав олександрійський учений Евклід. От і ми беремося до вивчення геометрії, основний матеріал якої викладений у цій книзі. Почнемо вивчення з розділу, що розглядає властивості фігур на площині (при цьому показую заздалегідь підготовлені моделі плоских фігур: трикутника, квадрата, кола й т.п.). Називається цей розділ планіметрія і походить від латинського слова рlапит — поверхня, площина та грецького теtrео — вимірюю.
Коли ми будемо зображувати різні фігури на класній дошці або в зошитах, то поверхні дошки й аркуша будемо вважати площиною, на якій розглядатимуться ці фігури.
Другий розділ геометрії — стереометрію, у якій розглядаються просторові фігури (демонструю кулю, куб, піраміду), ми будемо вивчати в старших класах.
Ознайомлення з структурою підручника.
Проводжу інструктаж по правилах техніки безпеки з креслярськими інструментами.
II.Оголошення теми та мети уроку. Мотивація навчання.
За переказами, біля входу до Академії Платона було написано “Та не ввійде сюди ніхто з тих, хто не знає геометрії”. З найдавніших часів геометрія вважалася однією з важливих компонент будь-якої освіти взагалі. Насамперед що таке геометрія?
Минали роки… геометрія збагачувалася новими фактами, змінювала свій вигляд. Були часи, коли вона, як при Платоні або Піфагорі, займала становище справжньої цариці наук, а були й періоди, коли вона в своєму розвитку починала відставати від інших, молодих, що бурхливо розвивалися, наук. Але ніколи, очевидно, поки стоїть світ, не настане такий час, коли б людство могло сказати: ось тепер геометрія не потрібна і залишається здати її в архів.
Геометрія була, є і буде постійною супутницею людини на всьому шляху її розвитку, у всій її довгій, складній і цікавій еволюції.
Отже, геометрія-це наука про властивості геометричних фігур.
Далі учні в зошитах під темою уроку роблять такі записи:
- Геометрія — це наука...
- Планіметрія — це розділ...
- Приклади геометричних фігур.
Незакінчені речення пропоную дописати вдома, використовуючи підручник, а також зробити рисунки кількох геометричних фігур і написати їхні назви.
ІІI. Вивчення нового матеріалу
Діти, які фігури вам відомі? Про які властивості їх можете розповісти?
Далі наголошую, що основними фігурами на площині є точка й пряма. Як уявляєте собі ці фігури? Точка-це єдина фігура, яку не можна розбити на частини.
При цьому варто зазначити, що пряма нескінченна, а на рисунку завжди зображують частину прямої; щоб розрізняти окремі точки або прямі, їм дають найменування: «точка А», «пряма а». Так уводяться позначення основних фігур. По ходу розповіді(пояснення відбувається за підручником Істер, геометрія, 7 клас) ,учні роблять у зошитах рисунки за схемою 1, підготовленою заздалегідь.
Схема 1
Розміщення основних геометричних фігур на площині
|
Рис. 1 |
Основні фігури: точка А і пряма а |
|
Взаємне розміщення точок і прямих на площині |
|
|
Рис. 2
Рис. 3 |
Аксіома
Яка б не була пряма, існують точки, що належать цій прямій (А Через будь-які дві точки можна провести пряму і тільки одну |
|
Взаємне розміщення прямих на площині |
|
|
Рис. 4 |
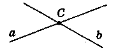
Прямі а і Ь перетинаються в точці С |
|
|
Прямі а і b паралельні (а || b) |
|
Рис. 5 |
|
Новим для учнів під час викладання матеріалу буде поняття «точка належить прямій». Наголошую, що той самий зміст мають слова «точка лежить на прямій», «пряма проходить через точку», потім уводжу знаки належності точок фігурі є та заперечення цієї належності ![]() .
.
Починаючи розглядати основні властивості найпростіших геометричних фігур, даю можливість учням самостійно, дослідним шляхом переконатися в наявності цих властивостей у даних фігур.
Запитання до класу
- Що зображено на рис. 2 схеми 1 [Точки й пряма.]
- Як розміщені точки відносно прямої (див. рис. 2 схеми 1)? [Є точки А і Б, що лежать на прямій, і точка С, що не лежить на ній.]
Чи можна побудувати ще такі точки? [Так.]
• Побудуйте кілька таких точок у своїх зошитах на рисунку. Формулюю першу основну властивість належності точок і прямих.
Під час розглядання другої властивості учням пропоную з'ясувати таке:
- Чи можна через одну точку провести пряму і якщо можна, то
скільки? [Можна. Безліч (рис. 1, а).]
- Чи можна через дві дані точки провести пряму? [Можна.]
- Чи можна провести пряму через будь-які дві точки (зазначається інше положення точок)? [Так.] .
- Скільки прямих можна провести? [Тільки одну (рис. 1,6).]
- Чи можна через три точки провести пряму і скільки?
У разі неповної відповіді на запитання ,цікавлюся чи є ще які-небудь варіанти розв'язання, а за необхідності-пояснюю. [Можна провести або одну пряму (рис. 1, б), або не можна провести жодної (рис. 1, г).]
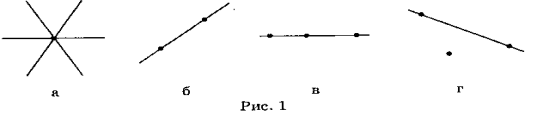
Висновок. Через одну точку можна провести одну та більшу кількість прямих; через дві точки можна провести тільки одну пряму; через три точки можна провести одну пряму, але не через будь-які три точки ,а тільки якщо вони розміщені, як показано на рис.1,в.
Звертаю увагу на таке:
- у формулюванні другої основної властивості містяться два твердження: про існування прямої, що проходить через будь-яку пару точок, виражене словами «можна провести», і про її єдиність «і тільки одну»;
- пряму можна позначати двома точками, через які вона проходить.
Трьом учням біля дошки пропоную розміститися так, щоб один із них стояв між двома іншими. Оскільки в учнів уже склалося інтуїтивне уявлення про поняття «між», то завдання не повинне викликати утруднень. Звертається увага на те, що всі троє стоять на одній прямій.
Запитання до класу
• Чи перебуває учень, що сидить за останньою партою, між двома іншими, які стоять біля дошки? [З'ясовується, що ні, тому що ці учні не розміщені на одній прямій.]
• А тепер, використовуючи рис. 6, зробіть висновки щодо точок А, В, С і точок А, С, D (рисунок заздалегідь заготовлений на дошці).
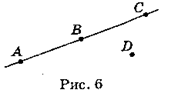
[Якщо точка В лежить між точками А і С, то всі три точки лежать на одній прямій; якщо точки А, С і D не лежать на одній прямій, то жодна з них не лежить між двома іншими.] Основна властивість взаємного розміщення точок на прямій
Для більш осмисленого засвоєння змісту аксіоми про розміщення точок на прямій пропоную завдання й запитання.
• Позначте на прямій три точки так, щоб одна з них лежала між двома іншими. Чи завжди це можливо? [Так.]
• Позначте на прямій три точки так, щоб жодна з них не лежала між двома іншими. [Учні переконуються, що зробити це не¬можливо.]
• Який із цього можна зробити висновок? [Із трьох точок на прямій хоча б одна лежить між двома іншими.]
• Чи можна розмістити на прямій три точки А, В і С так, щоб дві з них лежали між двома іншими? [Учні знову переконуються, що це зробити неможливо.]
• Який висновок можна зробити про три точки, що лежать на одній прямій? [Із трьох точок, що лежать на прямій, завжди тільки одна лежить між двома іншими.]
Формулює основну властивість розміщення трьох точок на прямій (аксіому). Наголошує, що у твердженні аксіоми фраза «одна й тільки одна» говорить:
1) про існування на прямій хоча б однієї точки (з трьох), яка має властивість лежати між двома іншими;
2) про єдиність такої точки, їх не може бути дві, три й т. д. Це додатково підтверджується словами «тільки одна».
Далі вчитель звертає увагу на те, що оскільки з трьох: точок на прямій дві не лежать між двома іншими, то кожна з них розміщена якось інакше відносно інших точок. Якщо, наприклад, точка Б лежить між точками А і С, то тоді можна сказати, що точки В і С лежать по один бік від точки А.
Первинне закріплення нових знань та вмінь учнів
Завдання класу
-
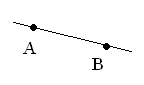
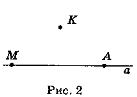
Поясніть взаємне розміщення точок А, М, К і прямої а (рис. 2). Запишіть висновок, використовуючи знаки
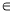 і
і 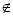 .
.
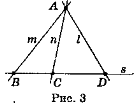
- Використовуючи рис. 3, дайте відповіді:
а) Яким прямим належать точки А, В, С і D?
б) Які прямі проходять через кожну з точок А, В, С, D?
в) Як інакше можна позначити прямі m, п і s?
г) Які точки лежать на прямих АВ і СD?
- Точки А і Б лежать на прямій l. Чи збігаються прямі АВ і 1? Поясніть відповідь. [Точки А і В належать прямій АВ і прямій l, а через дві точки можна провести тільки одну пряму. Отже, прямі АВ і l збігаються (рис.4).]
-
Чи будуть збігатися прямі АВ і l, якщо точка B не лежить на прямій l? Поясніть відповідь. [Не будуть. Якби ці прямі збігалися, то точка B належала б прямій l. А це суперечить умові задачі: точка В
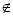 l (рис. 5).]
l (рис. 5).]
![]()
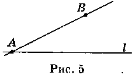
Звертаю увагу учнів на те, що в цьому випадку прямі вважаються різними, і робить висновок: прямі будуть різними, якщо хоча б одна точка однієї прямої не належить іншій прямій.
Задача 1 (усно). Відомо, що точка Р лежить між точками М і N. Як розміщені точки: а) М і N; б) М і Р; в) N і Р? [а) По різні боки від точки Р; б) по один бік від точки N; в) по один бік від точки М.]
Задача 2 (усно). Із трьох точок М, N і Р, що лежать на прямій, точки N і Р лежать по один бік від точки М. Яка точка лежить між двома іншими? [Точка М не лежить між точками N і Р. А оскільки кожна з точок МІР може лежати між двома іншими, то дати однозначну відповідь на запитання задачі неможливо.]
Наприклад, із твердження, що точка Р лежить між точками М і N, випливає твердження, що точки М і Р лежать по один бік від точки N (задача 1). Однак із того, що точки М і N лежать по один бік від точки N, ще не можна зробити висновок, що точка Р лежить між точками М і N (задача 2).
Робиться висновок. Якщо з трьох точок одна лежить між двома іншими, то всі три точки лежать на одній прямій, і навпаки, із трьох точок на прямій одна й тільки одна лежить між двома іншими (аксіома).
Пояснення матеріалу
Пояснюю основну властивість прямої.
Вводжу означення прямих, що перетинаються.
Формулюю теорему: будь-які прямі, що перетинаються ,мають спільну точку та доводимо її.
Вводжу поняття променя, доповняльного променя та позначення променів
V. Закріплення вивченого матеріалу
Практична робота
№4;
№7
VI. Підсумок уроку. Рефлексія.
« Мікрофон»
1.Що нового дізналися на уроці?
2.Для чого потрібні набуті знання?
3.Чи досягли мети уроку?
4.Що найкраще сподобалося на уроці ?
Завдання додому:
Незакінчені речення пропоную дописати вдома, використовуючи підручник, а також зробити рисунки кількох геометричних фігур і написати їхні назви.


про публікацію авторської розробки
Додати розробку