Геометричний проект. Складання задач за даними рисунками

Як скласти геометричну задачу за заданим малюнком

Хоч би як добре працювала машина,

вона зможе розв’язувати всі задачі,

 що ставляться перед нею,

але сама жодної задачі не придумає.

А. Ейнштейн

Поговоримо про використання одного з активних методів навчання – проект для учнів. Він демонструє застосування учнями профільного 11 класу своїх знань, умінь, творчого підходу до розв’язування планіметричних задач. Цінність цього проекту в тому, що учні не лише повторюють основні планіметричні формули, теореми, означення, властивості, але й самостійно складають задачі за запропонованими малюнками, самі приймають рішення щодо необхідної та достатньої кількості умов у задачах, повністю пояснюють хід розв’язку. А ще – це елемент розвитку профільного навчання у старшій школі, де учителі ще й досі шукають нові сучасні підходи до вивчення математики, тому, напевне, це питання зацікавить як молодих учителів математики, так і досвідчених насамперед своїм оригінальним підходом до повторення конкретних математичних питань. Також слід зазначити, що викладені у роботі з першої до останньої думки є суто авторськими (автора роботи і учнів 11 класу) та оригінальними, якщо так взагалі можна сказати про математичні вирази та викладки.

Під час повторення питань з планіметрії клас було розбито на 10 груп по троє учнів, серед яких один був лідером групи. Кожна група отримала готовий рисунок, за яким потрібно було скласти задачу, підібравши необхідні дані (букви або числа – на свій розсуд). Розв’язування повинно містити не менше 4-5 кроків, це дає потрібний рівень складності, що насправді досягається і самим малюнком. Потрібно було отримати «просту» відповідь, повністю розв’язавши і пояснивши хід розв’язання. Учителем були запропоновані малюнки, які стосуються, як правило, многокутника і декількох кіл у різних варіаціях. Подібних до цих задач у підручниках майже немає, тому запропоновані нижче задачі – це цілком самостійна творчість учнів.

Задача 1. У паралелограм вписано два кола, які дотикаються одне до одного і до сторін паралелограма (рис.1). Гострий кут паралелограма дорівнює 30^о. Знайти площу паралелограма, якщо радіуси даних кіл дорівнюють 3 см.

Роз’вязання: Розглянемо трикутник АВК. ВК дорівнює двом радіусам,

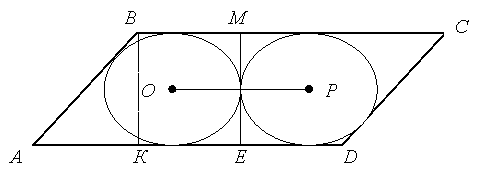                                           Рис.1

тобто ВК = 6 см, ВАК = 30^о за умовою. Тому АВ = 2ВК = 12 см (катет, що лежить навпроти кута 30^о дорівнює половині гіпотенузи). Проведемо дотичну до обох кіл МЕ. МЕАD, оскільки дотична МЕОР.

Трапеція АВМЕ прямокутна, вона описана навколо кола, тому

АВ + МЕ = АЕ + ВМ = 12 + 6 = 18.

Використовуючи те, що паралелограм є центральносиметричною фігурою, одержуємо рівності: ВМ = ЕD,  АЕ = МС.

Основа паралелограма АD = АЕ + ЕD = 18.

Площа паралелограма S = AD·BK = 18·6 = 128 (cм²).

Відповідь: 128 cм²

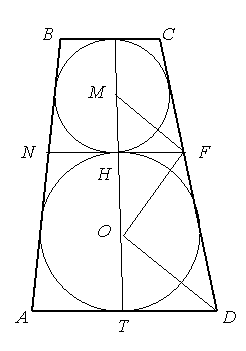
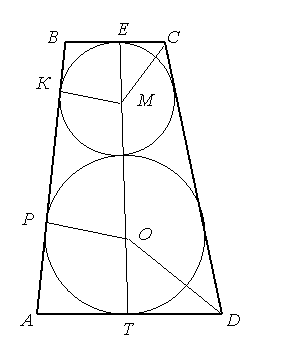Задача 2. У рівнобічну трапецію вписано два кола, які дотикаються одне до одного і до сторін трапеції (рис.2). Гострий кут трапеції дорівнює α, радіус більшого кола R. Знайти радіус меншого кола.

Роз’вязання: Нехай АВСD – дана рівнобічна трапеція, у якої ВАD = α (рис.2). Розглянемо ΔDOT: ODT = ,

OT = R, тому TD = Rctg . Маємо, що TD = AT = AP = Rctg. Оскільки МК та ОР – радіуси, проведені до точок дотику дотичної, то ОРАВ і МКАВ, а отже, МК||ОР, і чотирикутник КМОР – прямокутна трапеція, причому ОМ = R + x, КМ = х, де х – шуканий радіус меншого кола.

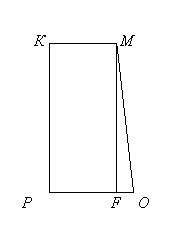
У трапеції КМОР (рис.3) проведемо                         Рис. 2

висоту МF = КР. У прямокутнику РКМF:

КМ = РF = х, а ОF = R – х.

У ΔМFО із теореми Піфагора слідує:

МF = = = 2.

Розглянемо ΔЕМС: ЕСМ = 90^о – , ЕМ = х, тому ЕС = хctg .

Враховуючи, що АВ = АР + РК + КВ, маємо бічну сторону трапеції

АВ = Rctg + 2 + хctg . ЕТ = 2R + 2х.

Очевидно, що ЕТ = АВsinα. Одержуємо рівняння, з якого знайдемо х.  

2R + 2х = Rctg sinα + 2 sinα + хtg sinα.

Перетворюючи праву частину рівняння, використовуємо формули:

sinα =2 sincos ,   tg , ctg .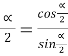

2R + 2х = 2R  + 4 sincos + 2хsin² . Розділимо обидві частини рівняння на 2R і зробимо заміну = t.

1+ t² = + 2t sincos +t²sin² , звідки

t² – 2t sincos + =0,

t² – 2t sincos +sin² = 0, або

=0, звідки t = tg.           

Враховуючи, що = t маємо х = R·tg²                                    Рис.3

Відповідь: R·tg²

Примітка. Попередній розв’язок був запропонований учнями. Здалось, що може бути інший, більш простий. Спільними зусиллями він був знайдений. Наведемо його (рис.4).

Проведемо NF||AD. CFH = CDT, як відповідні при паралельних прямих і січній. FM і DO – бісектриси цих кутів, MFH = ODT = .

У ΔMHF: HF = MHctg = xctg .

HFD = 180^o – α, з властивостей внутрішніх односторонніх кутів, HFО = 180^o – ,

оскільки FO – бісектрисa, а HОF = .

У ΔOHF: HF = OHtg = Rtg.

Маємо xctg = Rtg , звідки х = R·tg² .

Відповідь: R·tg²

Рис. 4

Задача 3. Два кола з рівними радіусами перетинаються. А і D – центри кіл. Пряма ВС, що паралельна прямій АD, перетинає обидва кола (рис.5). Довести, що АВСD – паралелограм.

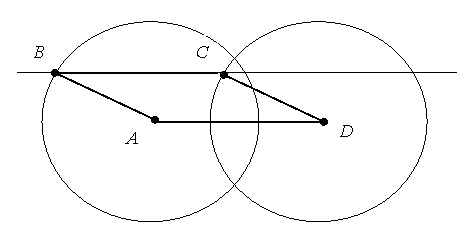
     Рис.5

Доведення. Якщо дві сторони чотирикутника паралельні і рівні, то такий чотирикутник – паралелограм. Виконаємо паралельне перенесення кола з центром D так, щоб його центр D співпав з центром другого кола А. При цьому кола співпадуть, а точка С співпаде з точкою В. Маємо, що DС||AB i DC = AB. Отже, АВСD – паралелограм.

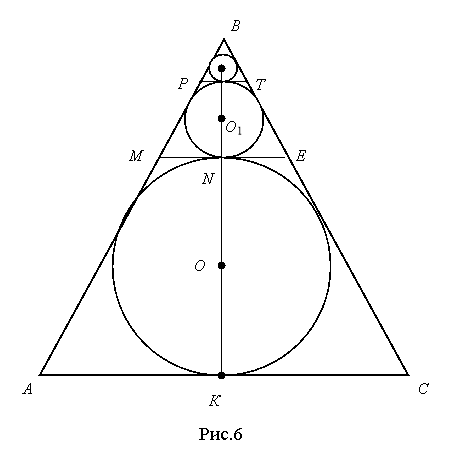Задача 4. У правильний трикутник зі стороною а вписано круг з центром О. На сторонах АВ і ВС трикутника взято точки М і Е так, що відрізок МЕ дотикається до круга. У трикутник МВЕ вписано круг з центром О₁. На сторонах МВ і МЕ трикутника МВЕ взято точки Р і Т так, що відрізок РТ дотикається до круга (рис.6). Таким чином вписується нескінченна кількість кругів. Знайти суму площ усіх цих кругів.

Розв’язання: Радіус круга, вписаного в правильний трикутник зі стороною а, дорівнює половині радіуса описаного навколо цього трикутника круга. Тому ОК = 0,5ВК, а ВN = ВК. Трикутники МВЕ і АВС подібні, оскільки правильні, усі їх лінійні елементи відносяться як 1: 3, а площі відносяться як 1: 9. Очевидно, що площі трикутників, вписаних заданим чином, утворюють нескінченну геометричну прогресію з b₁ = S_ABC, q = .

S_ABC = . Сума площ кругів S = = : = .

    Відповідь:

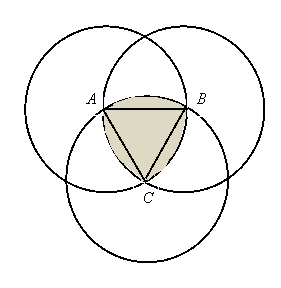Задача 5. Три круга з радіусами R перетинаються так, що їх центри знаходяться на перетині двох інших кіл (див. рис.7). Знайти площу виділеної фігури.

 

Роз’вязання: Проведемо хорди АВ, ВС і АС. Площа виділеної фігури дорівнює сумі площ рівностороннього трикутника АВС зі стороною R і трьох сегментів з відповідним центральним кутом 60^о.

Площа трикутника .

Площа одного сегмента .

Отже, площа виділеної фігури дорівнює

+3· = = .                                Рис.7

Відповідь:

 

Задача 6. Катети і гіпотенуза прямокутного трикутника є діаметрами трьох кругів. Доведіть, що площа більшого круга дорівнює сумі площ двох інших кругів.

Розв’язання: Нехай сторони прямокутного трикутника (рис.8) АВ = с, АС = b, ВС = а. Отже, а, b і с – діаметри кругів. Площа більшого круга дорівнює , сума площ двох інших кругів + = .

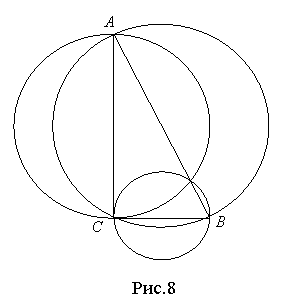ΔАВС прямокутний, тому за теоремою Піфагора c² = a² + b². Звідси =,

тобто площа більшого круга дорівнює сумі площ двох інших кругів, що й потрібно було довести.

 

Задача 7. У рівнобедрений трикутник з кутом при основі α вписано два кола з рівними радіусами r (рис.9). Знайти площу трикутника.

Роз’вязання: Проведемо висоту ВD до основи трикутника (зауважимо, що ця висота може перетинати тільки одне з кіл, або обидва кола в залежності від значення кута α). Із центрів кіл О і М проведемо перпендикуляри ОЕ та МК до сторони АВ. Ці перпендикуляри дорівнюють радіусам кіл r. ЕКМО – прямокутник, ОМ = ЕК = 2r. Знайдемо сторону АВ як суму відрізків АЕ, ЕК і КВ. Розглянемо трикутник АЕО. ОЕ = r, ЕАО = . Тому АЕ = rctg .

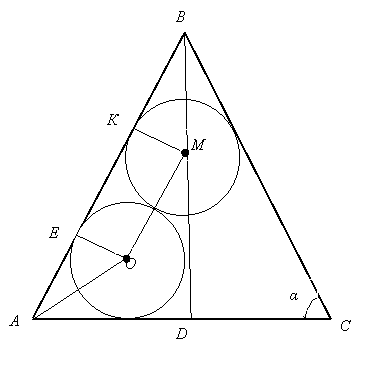     Рис.9

У трикутнику ВКМ МВК = 90^о – α, а ВМК = α. Тому ВК = rtgα. Отже, АВ = rctg + 2r + rtgα = r(2 + ctg + tgα).

Враховуючи, що АВС= = 180^о – 2α, знаходимо площу трикутника

S =  АВ·ВСsin(180^о – 2α) =   r²(2 + ctg+ tgα)²sin2α.

Відповідь:   r²(2 + ctg+ tgα)²sin2α.

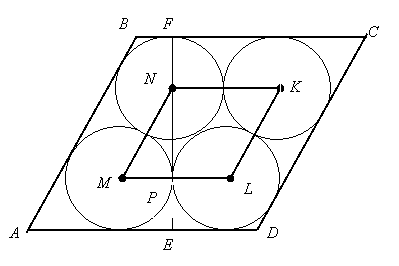Задача 8. Чотири кола однакового радіуса вписані у ромб так, що вони дотикаються один до одного (рис.10). Знайти відношення висоти ромба до радіуса кола.

Роз’вязання:

           Рис.10

Нехай радіус кола дорівнює r. Тоді висота ромба АВСD FE = FN + NP + PE = 2r + NP, оскільки NF = PE = r. Чотирикутник MNKL – ромб, оскільки усі його сторони дорівнюють по 2r. Менша діагональ ромба NL = 2r, тому ΔMNL – правильний, NML = 60^о. Із ΔMNP: NP = MN · sin60^o = 2r· = r. Тому висота ромба АВСD   FE = 2r + r = r(2 + ).

Шукане відношення FE : r = 2 +

Відповідь: 2 +

Задача 9. Коло з радіусом 16 см внутрішньо дотикається до більшого кола. Хорда АВ більшого кола дотикається до даного кола (рис.11) і точкою дотику ділиться навпіл. Знайти радіус більшого кола, якщо АВ = 32 см.

Роз’вязання: Оскільки діаметр СD проходить через точку дотику Е і ділить АВ навпіл, тобто АЕ = ЕВ = 16.

О – центр більшого кола. DЕ = 32 см. Нехай СЕ = х.

Відомо, що для хорд АВ і СD виконується рівність СЕ·ЕD = АЕ·ЕВ, звідси 32х = 16·16, а х = 8. Діаметр більшого кола СD = DЕ + ЕС = 32 + 8 = 40, тому його радіус 20 см.                           

      Рис.11

Відповідь : 20 см

Задача 10. Коло з радіусом 4 см і два кола з радіусами по 2 см дотикаються зовні так, що центри їх кіл лежать на одній прямій (рис.12). Проведені спільні дотичні до кіл АВ, ВС, СD, DА. Знайти площу чотирикутника АВСD.

Розв’язання. АВСD є центральносиметричною фігурою і фігурою, яка має вісь симетрії, тому АВСD є ромбом. Площа ромба дорівнює добутку сторони на висоту, причому висота дорівнює двом радіусам вписаного кола, тобто 8 см. Знайдемо сторону АD ромба.

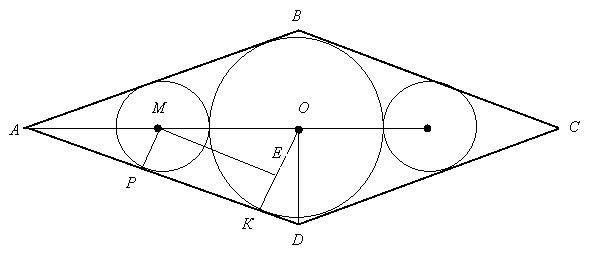          Рис.12

 

Проведемо радіуси кіл МР та ОК у точки дотику. МР АD, ОК АD, РМОК – прямокутна трапеція, основи РМ = 2 см, КО = 4 см, більша бічна сторона МО = 6 см (сума радіусів). Нехай МЕОК, тоді РМЕК – прямокутник, КЕ = 2 см, ЕО = 2 см, РК = МЕ.

Розглянемо прямокутний прямокутник МЕО. За теоремою Піфагора

МО² = МЕ² + ЕО², звідки МЕ² = МО² – ЕО² = 36 – 4 =32, а МЕ = РК = 4. Зауважимо, що ОDК = MОE = АМР. У трикутнику МОЕ знаходимо

tgMОE = = 2.

У трикутнику ОКD: КD = ОК:tgОDК = 4:(2) = .

У трикутнику АМР: АР = МР·tgОDК = 2·2 = 4.

АD = АР + РК +КD = 9 см.

Площа ромба S = 9·8 = 72 (см²).

                         Відповідь: 72 см²