Міністерство освіти і науки України

Донецький національний університет економіки і торгівлі

імені  Михайла Туган-Барановського

Краматорський технікум

 

 

 

 

 

 

 

 

 

Методична розробка

відкритого практичного заняття

Дисципліна: Вища математика

Тема заняття: «Границя функції»

Спеціальність: 5.03050401 «Економіка підприємства»

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2015р.

                                

Методична розробка практичного заняття з дисципліни «Вища математика». Підготувала  викладач Краматорського технікуму Донецького національного університету економіки і торгівлі імені Михайла  Туган-Барановського                                    Кулешова Н.М.

 

10.02.2015р.

 

Викладено методику проведення практичного заняття з використанням тренінгових технологій, що сприяє активізації уваги і мислення студентів, виховує відповідальність і  навички колективної та самостійної роботи з теми «Границя функції». 

 

 

Для викладачів вищої математики вищих навчальних закладів  І-ІІ рівня акредитації.

 

 

 

Рецензенти:

 

Грудкіна Н.С. - к.т.н., старший викладач кафедри вищої математики Донбаської державної машинобудівної академії

Гуляєва Л.П.- спеціаліст вищої кваліфікаційної категорії, викладач вищої математики Краматорського технологічного технікуму

 

 

 

Розглянуто і  схвалено на засіданні циклової комісії загальноосвітніх та природничо-наукових  дисциплін 

Протокол № 7 від 11.02.2015р.                                                                 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ЗМІСТ

 

Передмова…..……………………………………………………………………………...4

1. Методика проведення практичного заняття за темою  «Границя функції»

• 1.1. План заняття………………………………………………...…………..…...…..……5
• 1.2. Зміст проведення заняття..………...…………………………………….……...…....6
• 1.3. Методичне обґрунтування проведення заняття…………………………………….7
• 2. Література….………………………………………………………………..………......8

3. Додатки

1. Інструкційна карта…………………………………..……...…….…….…..……....9
2. Математичний диктант…………………………………………………………...11
3. Критерії  оцінки знань студентів ……………………………..…………............12
4. Відомість   обліку роботи студентів групи за практичне заняття………..……13

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Передмова

 

Підготовка молодших спеціалістів в області товарознавства та комерційної діяльності  передбачає ґрунтовні знання з математики і вміння їх застосовувати в майбутній професійній діяльності. Важливість і актуальність даної теми пояснюється тим, що при дослідженні тих чи інших економічних явищ необхідно вміти правильно використовувати математичні методи і моделі. Використання математики в економіці допомагає виділити й описати за допомогою формул найбільш важливі зв’язки між економічними змінними та об’єктами. Крім того, математика необхідна для успішного засвоєння фундаментальних та професійно спрямованих дисциплін, які забезпечують базові економічні знання та закладають основи для подальшого вивчення спеціальних дисциплін.

Вивчаючи розділ «Диференціальне числення функції однієї змінної» студенти спираються на знання та уміння, набуті в процесі вивчення курсу алгебри та геометрії загальноосвітньої школи.

Проведення практичного заняття за темою «Границя функції» дозволяє студентам спеціальності «Товарознавство та комерційна діяльність» засвоїти вміння застосовувати границю функції при обчисленні:

•      зміни ціни товару або закону зміни кількості покупців та продукції  в залежності від часу;
•      попиту при постійній еластичності;
•      росту економічних показників при постійному або спадному темпі приросту;
•      корисність при постійній схильності до ризику.

Практичне заняття проводиться у виді тренінгу та із застосуванням комп’ютерної техніки. Тренінг, як технологія навчання, дає змогу за короткий проміжок часу вирішити проблему інтенсивного формування та розвитку вмінь і навичок, щодо розрахунку границь функції, розвиває здатність систематизувати, аналізувати, робити висновки, формує вміння оперувати термінами математичного аналізу, розвиває  творчі здібності.

 

 

1. МЕТОДИКА ПРОВЕДЕННЯ ПРАКТИЧНОГО ЗАНЯТТЯ

1.        План заняття

Дисципліна:   Вища математика.

Тема заняття:  «Границя функції».

Тип заняття: Формування практичних вмінь і навичок.

Вид заняття:   практичне. 

Форма проведення: тренінг.

Група:   ЕП-14-Б.

Дата проведення:   26.02.2015р.

Мета заняття:

 

методична:  Удосконалити методику проведення практичного заняття з використанням інноваційних технологій.

 

дидактична: Сформувати практичні вміння та навички розрахунку границь функцій, які застосовуються при обчисленні зміни ціни товару або закону зміни кількості покупців та продукції  в залежності від часу; попиту при постійній еластичності; росту економічних показників при постійному або спадному темпі приросту; корисність при постійній схильності до ризику.

 

виховна: Сприяти формуванню пізнавального інтересу щодо застосування границі функції при розрахунку економічних показників підприємств торгівлі.

 

Методичне забезпечення заняття: Інструкційна карта (Додаток А), математичний диктант (Додаток Б), критерії  оцінки знань студентів (Додаток В),  відомість   обліку роботи студентів групи за практичне заняття (Додаток Г).

 

Технічні засоби навчання: ноутбук, мультимедійний проектор.

 

Міждисциплінні зв'язки:

1.           Дисципліна: Інформатика та комп’ютерна техніка.

 Тема: Вставка об’єктів в Ms Word.

2.           Дисципліна: Економіка торгівлі.

 Теми:  Товарні запаси підприємства; Нормалізація товарних запасів;

     Прибуток підприємства.

3.           Дисципліна:   Бухгалтерський облік.

 Тема: Облік доходів та витрат.

 

Внутрідисциплінні зв’язки:

Дисципліна: Вища математика

Тема: Похідна функції однієї змінної.

Тема:  Функції багатьох змінних.

 

 

1.2. Зміст заняття

1.  Організаційний момент:

1.       Привітання студентів.
2.       Перевірка наявності студентів в аудиторії.
3.       Перевірка готовності студентів до проведення заняття.

 

2.               Повідомлення теми, навчальних цілей заняття:

Тема: «Границя функції».

3. Мотивація навчальної (пізнавальної) діяльності студентів.

Визначення фундаментальних понять математичного аналізу дає можливість досліджувати процеси і явища в природних, соціальних і економічних науках, сприяє глибокому розумінню навколишніх процесів.

Однією із основних задач підприємств торгівлі є дослідження поведінки показників економічної діяльності. Використання математичного апарату значно полегшує задачу дослідження. Границя функції-основне поняття теорії аналізу.

4.               Підготовчий етап.

4.1. Актуалізація опорних знань за допомогою математичного диктанту                (Додаток Б).

4.2. Ознайомлення студентів з порядком проведення заняття.

5.               Основний етап проведення заняття.

Практичне заняття проводиться за допомогою інструкційної карти  (Додаток А).

6.               Заключний етап:

        6.1. Підведення підсумків заняття.

        6.2. Оцінювання діяльності студентів на занятті.

7. Домашнє завдання І.І. Литвин, ст. 62-63, №№ 24(5,8,9.10,13,15)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Методичне обґрунтування проведення заняття

 

Практичне заняття з використанням тренінгових технологій за темою «Границя функції» проводиться зі студентами спеціальності 5.03051001 «Товарознавство та комерційна діяльність».

Заняття починається з організаційного  моменту, який складається з привітання студентів та  перевірки наявності студентів в аудиторії.

При проведенні мотивації пізнавальної діяльності увага студентів звертається на те, що визначення фундаментальних понять математичного аналізу дає можливість досліджувати процеси і явища в природних, соціальних і економічних науках, сприяє глибокому розумінню навколишніх процесів. Однією із основних задач підприємств торгівлі є дослідження поведінки показників економічної діяльності. Використання математичного апарату значно полегшує задачу дослідження, а границя функції-основне поняття теорії аналізу.

Актуалізація опорних знань проводиться за допомогою математичного диктанту, який дає можливість перевірити теоретичні питання теми. На цьому етапі присутній елемент самоперевірки робіт за зразком, який висвітлюється на екрані.

Для опрацювання практичних завдань використовуються тренінгові технології, які передбачають індивідуальну роботу, роботу  у складі малих груп,  гру. Завдання надані в інструкційній карти (Додаток А).

Перше завдання спрямоване на формування практичних вмінь та навичок знаходження границь функцій при х→∞. Для встановлення рівня знань проводиться  бліц-вікторина з використанням комп’ютерної техніки.

Друге завдання передбачає знаходження границі функції в точці. Завдання сформовані у виді міні-тестів, що розвивають навички самостійної роботи. 

На наступному етапі заняття  кожна мала група отримує завдання обчислення границь функції,  що містять ірраціональність, які розв’язуються за  допомогою методу мозкового штурму. Представники груп записують результати на дошці. Виконання завдання спрямовано на виховання ініціативності, пізнавального інтересу, свідомого ставлення до навчання.

  Четверте завдання на обчислення границь функції методом заміни на еквівалентні,  передбачає проведення гри «Математичне доміно». Розв’язується приклад та співвідноситься результат з числом на картці. Ігровий момент сприяє формуванню уважності та наполегливості, привносить різноманітність у навчальний процес.

Кожній малій групі було надано заздалегіть завдання підготувати задачу для іншої групи щодо обчислення границі функції з використанням другої визначної границі. Для виконання п’ятого завдання студенти обмінюються завданнями та розв’язують їх. Результати повертають групі, яка надала задачу для перевірки. Домашня самостійна робота в групах допомагає розвивати комунікативні навички.

Наприкінці заняття підводяться підсумки, оцінюється робота студентів та надається домашнє завдання.

 

 

 

 

 

ЛІТЕРАТУРА

 

1. Дубовик В.П.Вища математика: Навч. посібник / В.П. Дубовик, І.І. Юрик – К. : Вища шк., 2001. – 648 с.
2. Вища математика: Збірник задач: Навч. посібник / В.П. Дубовик, І.І. Юрик [та ін.] – К. : Вища шк., 2003. – 480 с.
3. Вища математика: Підручник. У 2 ч. Ч. 1: Лінійна і векторна алгебра. Аналітична геометрія. Вступ до математичного аналізу. Диференціальне і інтегральне числення / Овчинников П.П. [та ін.] – К. : Техніка, 2003. – 600 с.
4. Вища математика: Підручник. У 2 ч. Ч. 2: Диференціальні рівняння. Операційне числення. Ряди та їх застосування. Стійкість за Ляпуновим. Рівняння математичної фізики. Оптимізація і керування. Теорія ймовірностей. Числові методи / Овчинников П.П. [та ін.] – К.: Техніка, 2000. – 792 с.
5. Данко П.Е. Высшая математика в упражнениях и задачах с решениями. В 2 ч. Ч. 1: Учебное пособие для вузов / П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова. – М. : ОНИКС 21 век, 2002. – 304 с.
6. Данко П.Е. Высшая математика в упражнениях и задачах с решениями. В 2 ч. Ч. 2: Учебное пособие для вузов / П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова. – М.: ОНИКС 21 век, 2006. – 416 с.
7. Высшая математика для экономистов: Учебник для вузов / Кремер Н. Ш. [и др.] – М.: ЮНИТИ, 2001. – 471 с.
8. Литвин І.І. та ін. Вища математика навчальний посібник. – К.: Центр навчальної літератури, - 2004. – 368с.

 

Інформаційні ресурси

 

1. http://mathsciences.at.ua/index/0-18
2. http://www.allmath.ru/highermath.htm
3. http://matem.com.ua/

http://uk.wikipedia.org/wiki/Вища_математика

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Додаток А

Інструкційна карта

до практичного заняття № 4

з дисципліни “Вища математика”

Тема: “ Диференціальне числення”

Тема практичного заняття: “Границя функції”

Мета: Сформувати вміння та навички обчислювати границю функції.

Методичні вказівки.

Властивовості границь функції:

1. 
2.  
3. 
4. 
5.    .

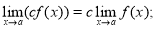
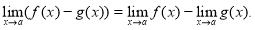
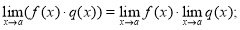
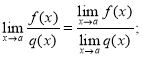
Невизначеності та методика їх розкриття.

1.Невизначеність 0/0 розв`язується в наслідку розкладу чисельника і знаменника на множники та скорочення дробі.

2.Невизначеність ∞/∞ розв`язується в наслідку ділення почленно чисельника та знаменника на більшу степінь невідомого та скорочення отриманих дробів.

3.Якщо границя ірраціональної функції  є невизначеність 0/0, ∞/∞ або ∞-∞, то чисельник і знаменник дробі помножують на вираз, спряжений з чисельником або знаменником та в наслідку застосовування формули різниці квадратів скорочують дріб.

Перша визначна границя і її наслідки

=1 –перша визначна границя 

=1; =1; =1; сos x=1;  sin x=0

 

Друга визначна границя і її наслідки

=е – друга визначна границя

=е =

Еквівалентності

а₀хⁿ+а₁х^n-1+а₂х^n-2+…+а_n ~ а₀хⁿ, при х→∞

~,при х→∞

sin a(x) ~ a(x)  наслідки першої 

tg a(x) ~ a(x)   важливої границі

arcsin a(x) ~ a(x) a(x) →0

arcsin a(x) ~ a(x)

 

Послідовність виконання завдання:

Завдання 1.    Знайти границі функцій при х→∞ 

1)lim   8х³-3х²+2х        2)lim   2х³-4х+5         3)lim          х³+1

     х→∞  4х³-2х+1              х→∞  х³+4                х→∞  2х²+2х-1

   4)lim     3х²-4         5)lim     2х³-3х²+4        6)lim  2х²-4х+8

      х→∞  х²+5х³             х→∞  -7х³-х²+5х             х→∞   х⁴+2х-1

 

 

Завдання 2. Розв’язати тестові завдання щодо знаходження границі функції при x→а   та скласти слово із відповідей. 

 

1 ВАРІАНТ 1. lim  3x2        x→0     x3 2. lim   4-x2                                    x→2   x-2 3. lim  x2-3x+2                                    x→1    x2-x Відповідь: -4-і            0-а ∞-с            8-у 3-н            -1-к   -3-м           27-п	2 ВАРІАНТ 1. lim  5x2                                    x→0     x 2. lim   9-x2                                    x→-3  x+3 3. lim  x2-6x+5                                    x→5    x2-5x Відповідь: 0-л           8-л 6-і            ∞-н  3-к           0,8-с -4-а          125-б
3 ВАРІАНТ 1. lim  2x4                                    x→0     x7 2. lim   1-x                                    x→1  x2-1 3. lim     x2-4х                                    x→3 x2-5x+4 Відповідь: -0,5-у      7-а -2-о        -7-с 1,5-к       9-н ∞-ж        3-м	4 ВАРІАНТ 1. lim  6x2                                    x→0    2x 2. lim   4-x2                                    x→2   2-х 3. lim       x2-x                                    x→1  x2-7x+6 Відповідь: 4-у         81-н 3-а         -0,2-б 0-к         -18-о ∞-м         9-е

 

Завдання 3.  Обчислити границі функцій, що містять ірраціональність:

1 група: 

2 група: 

3 група:  (-)

4 група:  (-)

Завдання 4. «Математичне доміно» .  Знайти границі функцій із застосуванням першої визначної границі та алгебраїчних перетворень. Розташувати картки за правилом доміно.

 

 

 

 

 

 

 

 

 

 

 

Завдання 5. Виконання завдань, підготовлених заздалегіть студентами груп на використання другої визначної границі. 

 

Додаток Б

 

Математичний диктант.

1 варіант 

1.Що називається границею функції?

2. Записати першу визначну границю та її наслідки.

3. Перелічити еквівалентності.

4. Що називається нескінченно малою функцією?

2 варіант 

1.Записати властивості  границь.

2. Записати другу важливу границю та її наслідки.

3.Невизначеності та методика їх розкриття.

4.Що називається нескінченно великою функцією?

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Додаток В

 

КРІТЕРІЇ ОЦІНЮВАННЯ

 

Засвоєння навчального матеріалу і навчальна діяльність з даної теми вищої математики  мають різнорівневий характер:

І – початковий, коли студент у результаті вивчення навчального матеріалу може назвати математичний об’єкт (вираз, формулу, символ), але тільки в тому випадку, коли цей об’єкт (опис, характеристика) запропонований йому безпосередньо.

ІІ – середній рівень, коли студент може відтворити інформацію, операції, дії, засвоєні ним у процесі навчання.

ІІІ – достатній рівень, коли студент уміє виконувати математичні операції, загальна методика і послідовність яких  йому знайомі, але зміст та умови змінені.

ІV – рівень творчості, коли студент здатний самостійно орієнтуватися в нових для нього ситуаціях, складати план дій і виконати його, пропонувати нові, невідомі йому раніше розв’язки тобто його навчальна діяльність носить дослідницький характер.

  Засвоєння навчального матеріалу і формування навчальної діяльності студентів підпорядковане принципу ієрархія рівнів, коли студент не може вийти на новий, не оволодівши навчальними елементами  на попередньому рівні.

  Оцінювання якості математичної  підготовки студентів з математики  здійснюється в двох  аспектах: рівень володіння теоретичними знаннями, який можна виявити в процесі усного та письмового опитування, та якість практичних умінь і навичок, тобто здатність до застосування вивченого матеріалу під час ровя´зування  задач і вправ.

 

І.Початковий (оцінка «2»)  

-співвіднести дані або словесно описані математичні об´єкти за їх суттєвими властивостями

- за допомогою викладача виконувати елементарні завдання

 

ІІ. Середній. (оцінка «3»)    

-ілюструвати означення математичних понять, теорем і правил виконання  математичних дії власними  прикладами .

-самостійно розв’язати  і пояснити розв’язання завдання (до 3-х кроків)

- записати математичний вираз, формулу за словесним формулюванням і навпаки

            

ІІІ Достатній(оцінка «4») 

-вільно володіє визначеним програмою навчальним матеріалом.

-розв’язує завдання з достатнім поясненням.

- самостійно виконує завдання в знайомих ситуаціях.

-виправляє допущені помилки.

 

ІV Високий   (оцінка «5»)

-виявляє варіативність мислення і раціональність у виборі способу розв’язання математичної проблеми.

-вміє узагальнювати  й систематизувати набуті  знання.

-здатний до розв’язування  нестандартних задач і вправ.

     

 

 

 

 

 

 

 

 

 

Додаток Г

Відомість   обліку роботи студентів групи за практичне заняття

 

№	П.І.Б.	1 завд. (1б)	2 завд. (1б)	3 завд. (1б)	4 завд. (1б)	5 завд. (1б)	Підсумки