ГРА «По дорозі к дробам»

 

Позакласний захід для учнів 6 класу

ГРА «По дорозі к дробам»

 

Задоволення, яке ми отримуємо від музики,

корениться в рахунку, але в рахунку неусвідомленому.

 Музика - це неусвідомлена арифметика, і більше нічого.
Готфрід

Ця гра проводиться в рамках тижня математики в 6 класі за участю  учнів 9 класу. Перед уроком учням 6-го класу були дані завдання підготувати, використовуючи додаткову літературу, повідомлення про історію виникнення дробів, цікаві задачі.

Мета: прищеплювати інтерес до математики; формувати навички ро­боти з додатковою літературою; поглиблювати знання про дроби і розви­вати навички виконання дій з дробами.

На першому з двох спарених уроків учні ознайомили клас зі своїми повідомленнями і задачами, цікаво й різноманітно оформленими. Ці ро­боти були оцінені вчителем і журі у складі учнів з 9 класу.

Слово вчителя. Діти, сьогодні ми здійснимо незвичайну подорож, ми з вами відвідаємо Країну Дробів. Там ми зробимо кілька зупинок у селищі Історичному, на березі озера Ребусного, відпочинемо на галявині Теат­ральній, побродимо в лісі Казковім, спробуємо подолати гори Мозкодром. На кожній зупинці слід показати свої знання і кмітливість. За правильні відповіді команди будуть одержувати жетони, а в кінці подорожі ми визна­чимо команду-переможницю. Маршрут ви будете обирати самі.

Отже, в путь! На першому уроці ми вже побували з вами в селищі Істо­ричному, ви розповідали цікаві історії, а зараз члени журі повідомлять вам про виникнення дробів.

 

Селище Історичне

I. Дроби з'явилися в сиву давнину. Під час розподілу здобичі, вимірюючи величини, та в інших схожих випадках люди зустрілися з необхідністю ввести в обчислення дроби.

Давні єгиптяни вже знали, як поділити два предмети на трьох, для числа - у них був спеціальний знак. Між іншим, це був єдиний дріб у вжитку єгипетських писарів, у якому в чисельнику не стояла одиниця. Усі інші дроби мали в чисельнику одиницю (їх називали основними дробами: ).

Якщо єгиптянину треба було використати інші дроби, він представляв їх у вигляді суми основних дробів.

 

II. У Давньому Вавилоні перевагу віддавали постійному знаменнику, що дорівнював 60. Римляни також користувалися лише одним знаменником, що дорівнював 12. Особливе місце займали дроби Справа в тому, що в давнину окрема арифметична операція передбачала подвоєння і ділення навпіл.

 

III. Дії над дробами в середні віки вважалися найскладнішою частиною математики. Донині про людину, що потрапила в скрутне становище, говорять: «Потрапив у дроби». Щоб полегшити дії з дробами, були вигадані десяткові дроби, в Європі їх увів у 1585 році голландський математик та інженер Симон Севін. У Франції десяткові дроби ввів у 1579 році Франсуа Вієт.

Слово вчителя. Діти, ви познайомилися з історією звичайних та десяткових дробів, а тепер настав час продовжити подорож. Наш шлях прямує до озера Ребусного.

 

 

Озеро Ребусне

Командам пропонується заповнити кросворд та розшифрувати дві анаграми. Команди отримують жетони. Команда-переможниця (яка отримала найбільше жетонів) обирає маршрут.

1. КИЬЛЧНСИЕ 2. ПРІЦЯОРОП

По горизонталі:

1. Ділення чисельника і знаменника на одне і те ж число.
2. На скільки скорочується дріб ?
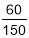3. Частка двох чисел.
4. Результат ділення двох чисел.
5. Дріб, у якого чисельник і знаменник — взаємно прості числа.

 

По вертикалі:

6. Назва дробу, в якого чисельник більший або дорівнює знаменнику.
7. Для скорочення дробу слід знаходити ....
8. Для знаходження спільного знаменника слід знаходити ....
9. Дія, за допомогою якої знаходимо дріб від числа.
10. Сота частина від числа.

 

Команди отримують жетони. Команда-переможниця (яка отримала найбільше жетонів) обирає маршрут.

 

Гори Мозкодром

1. Як,  переклавши один сірник,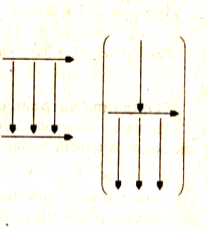одержати число, що дорівнює ?
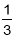2. Кожна команда отримує картку із завданням — поставити знаки дій так, щоб рівності були пра­вильними:

 

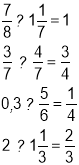
3. Розділіть сім кавунів на 12 осіб, зробивши якнайменше розрізів.

Команди отримують жетони. Команда-переможниця (яка отримала найбільше жетонів) обирає маршрут.

 

Ліс Казковий

Кожна команда отримує картку із завданням: виконати дії по порядку й розшифрувати прізвище відомої дитячої письменниці:

 

 

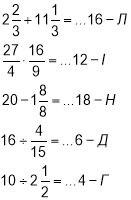
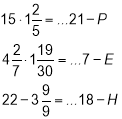
Галявина Театральна

До цього конкурсу діти готувалися заздалегідь. Вони показували сценки, казки, інсценували вірші про дроби. Ось деякі з виступів.

 

ПРОСТИЙ ДРІБ

У чисельника і знаменника постійні суперечки. Ніяк не зрозумієш, хто з них має рацію. Чисельник доводить одне, а знаменник перевертає на свій лад.

Чисельник. Я стою вище, то чому ж я менший за знаменник?

Знаменник. У мене число більше, то чому ж я мушу нижче стояти?

Ціле число, якому це базікання набридло, сказало їм прямо в очі: «Знайшли через що сперечатись! Погляньте, скільки навколо вас нерозв'язаних прикладів і задач!».

Знаменник. Тобі, Цілому, добре.

Ціле число. А хто вам заважає стати цілим числом? Складіться з яким-небудь дробом.

Чисельник. Гаразд, обійдемося без ваших задач та прикладів. І Знаменник. Йди, поки ціле!

Ціле число махнуло на них рукою і взялося за чергові задачі. Чисельник пере-I хилився, постукав у рисочку.

Чисельник. Послухайте, може, нам дійсно з іншим дробом скластися?

Знаменник. Е, ні, брате, годі жартів, досить з мене й одного Чисельника.

Чисельник. Якщо вже на те пішло, з мене теж одного знаменника І більш ніж достатньо.

Ще трохи подумали. Потім знаменник став навшпиньки, постукав і у рисочку.

Знаменник. Агов, друже! А якщо нам просто стати цілим числом, І без іншого Дробу?

Чисельник. Можна спробувати.

Стали вони пробувати. Чисельник помножився на 2, і знаменник — теж на 2, не відставати ж! Чисельник помножився на 3, і знаменник — настільки ж. Помножувалися, помножувалися, знесилили зовсім, а користі — ніякої. Той самий дріб, ні менший, ні більший за попередній.

Знаменник. Стій! Досить помножуватись. Давай ділитися. Так краще буде.

Стали ділитися. Знаменник на 2 і чисельник на 2. Знаменник на 3 і чи­сельник на 3. А дріб той самий і залишився.

 

Інсценування вірша

Прийшов зі школи наш Данило,

Щоденник заховав уміло.

Та враз побачила це мати —

Що ж, доведеться показати ...

Зітхнула матінка повільно,

Бо там — ого! — «незадовільно»

— Я не повірила б нізащо,

— Що в мене син — таке ледащо!

— За що отримав одиницю? —

Данилові морга сестриця.

— Сказав я, що гіпотенуза —

То особливий вид медузи...

— Ти ще й на двійку потрудився? —

В розмову батько тут втрутився.

— Отож, учителька завзята

Про землекопів і лопати

Чомусь задачку задала.

І де вона її взяла?

Я біля дошки, як умів,

її розв'язував, аж впрів,

І ось — закінчена робота —

Два і дві треті землекопа

У мене вийшло.

Я старався!

Тільки чому весь клас сміявся?

— Ой, горе, йди-но краще спати! —

Данилові сказала мати.

Заснув хлопчина. Та вночі,

Коли кричать одні сичі,

Йому приснився сон страшний — •

Десь на галяві лісовій,

Серед пахучої трави —

Лежав без ніг і голови

Його нещасний землекоп...

Хто б допоміг йому?

Ну, хто б?

Схопивсь Данило, стрепенувсь:

— Ой, матінко моя!

Тепер вже точно присягнусь,

Що дроби вивчу я!

 

На цьому урок закінчився, журі підбиває підсумки конкурсу і роздає жетони. Переможцем гри вважається та команда, яка набрала найбільшу кількість жетонів. Переможці одержують диплом.