Урок  алгебри в 7 класі  

Тема. Системи лінійних рівнянь.

                                          Методичну розробку уроку здійснила

                                          Брусняк Олександра Олександрівна,

                                          учитель математики вищої категорії.

                                          Загальноосвітня школа І –ІІІ ступенів №63

                                                    м. Маріуполь

                                          ВСТУП.

    Для кращого засвоєння теоретичного і практичного матеріалу математичні поняття та навички потрібно формувати з використанням не лише абстрактних, а реальних об’єктів. Цю складну функцію можна успішно здійснити шляхом посилення ролі практичних завдань при навчанні в групах.

    Структура пізнавальної діяльності учнів під час виконання практичних робіт з математики може бути такою.

1. Отримання навчально-практичного завдання.
2. Виконання практичного завдання.
3. Узагальнення результату, отриманого в процесі виконання роботи.
4. Абстрагування, тобто формування  математичних понять та навичок.
5. Систематизація та інтерпретація математичних знань.

Виконання завдання і узагальнення отриманих результатів приводять учнів до розвиваючої діяльності, при цьому нові знання не надходять із зовні, а є внутрішнім продуктом практичної діяльності учнів в системі інтерактивного метода «Навчаючи – навчаюсь». Отже, через виконання групових практичних робіт можна виховувати в учнів здатність абстрактно і конкретно мислити, навчати їх строгих дедуктивних доведень, формувати і закріплювати технічні навички й уміння( обчислювальні та алгоритмічні), взаємодопомоги. Дана розробка уроку має на меті розкрити деякі аспекти використання сучасних інформаційних технологій під час вивчення алгебри в 7 класі.

    БРУСНЯК ОЛЕКСАНДРА ОЛЕКСАНДРІВНА,

            УЧИТЕЛЬ МАТЕМАТИКИ, УЧИТЕЛЬ ВИЩОЇ КАТЕГОРІЇ

                                   УРОК АЛГЕБРИ В 7 КЛАСІ.

ТЕМА. СИСТЕМИ ЛІНІЙНИХ РІВНЯНЬ.

МЕТА. УЗАГАЛЬНИТИ ЗНАННЯ УЧНІВ ПРО СИСТЕМИ ЛІНІЙНИХ

               РІВНЯНЬ ТА МЕТОДІВ ЇХ РОЗВ’ЯЗУВАННЯ; ВЧИТИ  ВИКОРИ-

               СТОВУВАТИ ГЕОМЕТРИЧНУ ІНТЕРПРЕТАЦІЮ РІШЕННЯ

               СИСТЕМИ ПРИ РОЗВ’ЯЗУВАННІ ЕКСТРЕМАЛЬНИХ ЗАДАЧ,

               СФОРМУВАТИ УЯВЛЕННЯ ПРО ТАКІ ВАЖЛИВІ ПОНЯТТЯ, ЩО

               ВИКОРИСТОВУЮТЬСЯ В ЕКОНОМІЧНОМУ  СУСПІЛЬСТВІ, ЯК

               ЕФЕКТИВНІСТЬ, ОПТИМАЛЬНІСТЬ,  ВИГІДНІСТЬ; ПОКАЗАТИ, ЯК З

               ВИКОРИСТАННЯМ КОМП’ЮТЕРА МОЖЛИВО РОЗВ’ЯЗУВАТИ

               ЗАДАЧИ ЗА ТЕМОЮ УРОКУ; ФОРМУВАТИ НАВИЧКИ ЛОГІЧНО-

               ГО МИСЛЕННЯ, УМІННЯ АНАЛІЗУВАТИ І РОБИТИ ВИСНОВКИ;

               ЗАСТОСОВУВАТИ НА  ПРАКТИЦІ ІНФОРМАЦІЙНІ ТЕХНОЛОГІЇ,

               ПРОВОДИТИ КОМПЛЕКСНІ ФІЗИЧНІ ВПРАВИ ПРОФІЛАКТИКИ

               ВТОМИ  ОРГАНІЗМУ.

ТИП УРОКУ. КОМПЛЕКСНЕ ЗАСТОСУВАННЯ ЗНАНЬ ТА СПОСІБІВ ДІЙ.

ВИД УРОКУ. КОМБІНОВАНИЙ.

ЗАБЕСПЕЧЕННЯ. ПЕРСОНАЛЬНІ КОМП’ЮТЕРИ, ВАРІАНТИ ЗАВДАНЬ,

                                    ПРОГРАМА DB Wincalc for Windows.

КОМЕНТАР ДО ВЕДЕННЯ УРОКУ. УРАХОВУЮЧИ СПЕЦИФІКУ

                                                                ОЗДОРОВЧИХ КЛАСІВ, ПІД ЧАС УРОКУ У

                                                                 ХОДІ  ГРУПОВОЇ РОБОТИ ВЧИТЕЛЬ ОРГА-

                                                                 НІЗУЄ ДИНАМІЧНЕ ПЕРЕСУВАННЯ УЧНІВ

                                                                  І ПРОВОДИТЬ ФІЗИЧНІ РОЗМІНКИ НА

                                                                 ЗНІМАННЯ НАПРУГИ З ОПОРНО-РУХОМОЇ

                                                                  СИСТЕМИ ТА ОЧЕЙ ПРИ РОБОТІ З ПК.

                                     ХІД УРОКУ

І.Актуалізація опорних знань учнів.  Запитання.

1. Що називається рішенням системи рівнянь з двома невідомими?

2. Які методи вирішення систем вам знайомі?

3. Який зв’язок між коефіцієнтами при невідомих, вільними членами та

      рішенням системи?

(Учні дають усні відповіді).

ІІ. Розв’язування вправ.

    Клас ділиться на 4 групи, у кожній групі учні самі призначають головного;

роздаються завдання групам, і починається робота щодо їх виконання.

Роботу групи №1 контролює головний групи №2, роботу групи №2 - головний групи №1; так само здійснюється контроль в групах №3 і №4. Після закінчення виконання завдань учень, який здійснював контроль, стисло доповідає про участь кожного члена групи під час виконання завдання і якість цього виконання.

Завдання групи №1 (в групі 6 учнів)

Розв’язати системи рівнянь, після чого зобразити послідовно на координатній площині точки – рішення систем, поєднати їх послідовно. Отриману лама-

ну АВСDЕ відобразити симетрично вісі Ох. Кожен учень одержує для розв’я-

зування систему рівнянь. Якщо при виконанні завдання він зазнає труднощів, то має можливість звернутися до інших членів(у т. ч. до керуючого) групи для одержання допомоги або

консультації.

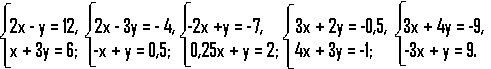
   Точка А     Точка В     Точка С         Точка D          Точка Е

Після вирішення системи учень пише відповідь на аркуші, передає його учню, який контролює роботу групи, а останній у свою чергу на зворотній стороні крила дошки зображує її як точку на координатній площині; точки А,В,С,D,Е

він послідовно з’єднує й отриману ламану відображає симетрично вісі Ох.

Після закінчення роботи група проводить фізрозмінку з елементами дихальної гімнастики.

Завдання групи №2 (в групі 6 учнів)

Кожен учень групи має виконати одне завдання за допомогою комп’ютера. Якщо при виконанні завдання він зазнає труднощів, то має можливість звернутися до інших членів групи(у т. ч. до керуючого) для одержання допомоги або консультації.

Дані системи рівнянь:

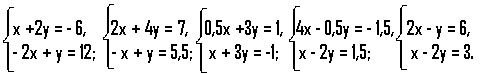
  Задати кожне рівняння системи як лінійну функцію, записати отримані формули мовою середовища програми DB Wincalc for Windows, за допомогою цієї програми та комп’ютера розв’язати графічно систему.

   Після вирішення системи учень пише відповідь на аркуші, передає його учню, який контролює роботу групи, а останній у свою чергу на зворотній стороні крила дошки зображує її як точку на координатній площині; точки А,В,С,D,Е він

послідовно з’єднує й отриману ламану відображає симетрично вісі Ох.

Після закінчення роботи група проводить фізрозмінку з елементами гімнастики на зняття зорової напруги.

  Результати роботи  груп №1 і №2 учні дивляться на зворотних крилах дошки, зображення мають бути симетричними відносно вісі Оу.

Завдання групи №3 на дошці (в групі 5 учнів)

  1. Замість знака питання вставити пропущене число.

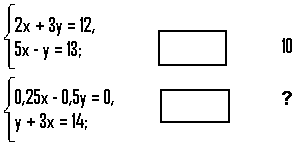
 Наслідком дій буде пара чисел, яка виявляється довжиною і шириною прямокутника. Шукане число – периметр прямокутника, тобто 12.

  2. Який малюнок треба зобразити замість знака питання ?

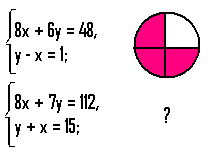
 Розв’язком першої системи є пара чисел (3;4). Заштриховано три чверті круга.

Розв’язок другої системи – (7;8), тому треба зобразити круг і заштрихувати сім восьмих його.

Завдання групи №4 на дошці  (в групі 5 учнів)

 1. Записати число замість знака питання.

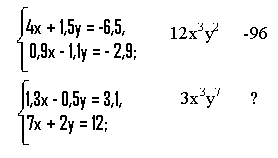
Розв’язком першої системи є пара чисел (-2;1), тоді значенням виразу є чис-

ло  -96.  Розв’язком другої системи є пара чисел (2;-1), тоді  замість знака ’?’ треба поставити число  -24.

  2. Записати невистачену  систему.

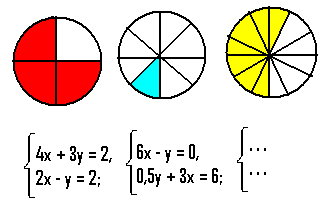
Розв’язком першої системи є пара чисел (3;4),тому в крузі заштриховано три чверті його.  Розв’язком другої системи є пара чисел (1;6), тому заштриховано одну шосту круга. Таким чином, необхідно записати систему, розв’язком якої є пара чисел (7;12).

 Після закінчення роботи група проводить фізрозмінку на знімання напруги з очей.

  Учні, які керували роботою кожної групи, стисло доповідають зміст завдань та демонструють на дошці результати  на їх виконання. Крім того, вони оцінюють роботу членів групи, а вчитель оцінює цих керуючих на результати їх власної роботи та роботи групи, якою вони керували.

ІІІ. Колективна робота по розв’язку задачі прикладної спрямованості.

ЗАДАЧА

Компанія з виробництва водяних фільтрів має фіксовані витрати, необхідні для постійного відтворення виробництва відповідної продукції у розмірі 20 000 грн.

При цьому витрати на виробництво одиниці продукції оцінюються в 20 грн., а ціна продажу одиниці продукції встановлена в розмірі 30 грн. Знайти  функцію щомісячних витрат, доходу, прибутку компанії.

  Розв’язання.

  Нехай х – кількість одиниць виробленої та проданої продукції. Тоді маємо функцію витрат - С(х), функцію доходу - R(х), функцію прибутку(збитку) - Р(х), де С(х) = 20х + 20 000; R(х) = 30х; Р(х) = R(х) – С(х) = 30х – (20х +20 000) =

  =  10х – 20 000.

   Визначимо щомісячну кількість виробництва та продажу водяних фільтрів, яка забезпечує рівновагу витрат та доходу.

    Для рівноваги доходу та витрат необхідно, щоб виконувалась рівність :

С (х) = R(х), тобто 20х + 20 000 = 30х, тоді х = 2000.

 R(2 000) = 3^. 2 000 = 60 000. Задача має точку рівноваги Р(2000; 60 000).

  Компанія може виробляти 2000 фільтрів з доходом та витратами 60 000 грн.

 Розглянемо на цьому прикладі можливості компанії, використовуючи графіки лінійних функцій у =С(х) і у = R(х). На дошці зображені графіки цих функцій.                           

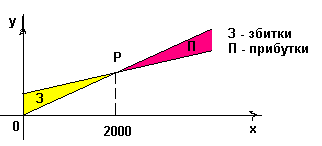
  Геометрично точка рівноваги Р є точкою перетину графіків функцій доходу та витрат.

Зауважимо, що при х < 2000 маємо  R(х) < С(х), тобто Р(х) = R(х) – С(х)<0, і компанія несе збитки. Коли х > 2000, тоді Р(х) > 0, і компанія отримує прибутки.

ІV. Підсумок уроку. Повідомлення домашнього завдання.

      Учні повідомляють, що на уроці вони повторили деякі методи розв’язування систем лінійних рівнянь, їх прикладну спрямованість. Комп’ютер допомагав їм у розв’язанні  завдань. Учитель називає результати навчальних досягнень учнів та оголошує домашнє завдання.