Урок "Формули зведення"
Тема заняття: Формули зведення.
Мета заняття: Вивчення формул зведення, формування умінь студентів
застосовувати вивчені формули для спрощення виразів та обчислень.
Обладнання: підручники, опорні схеми і таблиці.
Тип заняття: комплексного характеру
Література:
1. Алгебра і початки аналізу. Підручник для 11 кл. загальноосвітніх навчальних закладів, М.І. Шкіль, З.І. Слєпкань, О.С. Дубинчук. – К.: Зодіак – ЕКО, 2002, - 272 с.
2. Алгебра і початки аналізу: Підручник для 10-11 кл. загальноосвітніх навчальних закладів. – К.: Освіта, 2006. – 255с.
План заняття
I. Організація початку заняття.
II. Актуалізація опорних знань.
- Усне опитування студентів;
- Виконання усних вправ;
- Перевірка домашнього завдання.
III. Мотивація навчальної діяльності, повідомлення теми, мети заняття.
IV. Вивчення нового матеріалу:
- Сприймання і усвідомлення формул зведення.
- Виконання вправ
V. Підведення підсумків заняття.
VI. Домашнє завдання.
Хід заняття
I. Організація початку заняття.
II. Актуалізація опорних знань.
Питання до усного опитування:
1. Назвати основну тригонометричну тотожність.
2. Як можна з основної тригонометричної тотожності виразити ![]() і навпаки.
і навпаки.
3. Які ще співвідношення між тригонометричними функціями одного і того самого аргументу існують?
Виконання усних вправ.
Чому дорівнює вираз .![]() ;
; ![]() ;
; ![]() ;
;
Обчисліть: ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
;
![]()
Відповіді на питання студентів, що виникли в процесі виконання домашнього
завдання.
III. Мотивація навчальної діяльності, повідомлення теми, мети заняття.
IV. Вивчення нового матеріалу.
Сприймання і усвідомлення формул зведення.
Кожну тригонометричну функцію кутів ![]() ± α, π ± α,
± α, π ± α, ![]() ± α, 2π ± α можна виразити через тригонометричну функцію кута α. На цьому заняття ми розглянемо деякі такі формули.
± α, 2π ± α можна виразити через тригонометричну функцію кута α. На цьому заняття ми розглянемо деякі такі формули.
Нехай α – довільний кут, виражений у радіанах. На одиничному колі йому відповідає певна точка А, а куту ![]() - α – точка В.
- α – точка В.
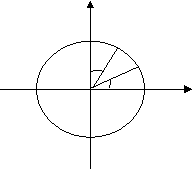 Опустивши перпендикуляри АК на вісь х і ВL
Опустивши перпендикуляри АК на вісь х і ВL
у на вісь у, дістанемо два рівних трикутника АОК
В і ВОL (![]() АОК =
АОК = ![]() ВОL, ОА = ОВ). Тому
ВОL, ОА = ОВ). Тому
![]()
![]() L α А ОL = ОК і ВL = АК, тобто
L α А ОL = ОК і ВL = АК, тобто
α
 О К
О К
sin (![]() - α) = ОL = ОК = cos α
- α) = ОL = ОК = cos α
мал 1 cos (![]() - α) = ВL = АК = sin α
- α) = ВL = АК = sin α

![]() Кутам
Кутам ![]() + α і
+ α і ![]() - α на одиничному колі відповідають точки, симетричні відносно осі у (мал. 2). Їх ординати рівні, абсциси протилежні. Тому у
- α на одиничному колі відповідають точки, симетричні відносно осі у (мал. 2). Їх ординати рівні, абсциси протилежні. Тому у
![]()
![]()
![]()
![]()
![]() С В sin (
С В sin (![]() + α) = sin (
+ α) = sin (![]() - α) = cos α
- α) = cos α
![]()
![]()
![]() cos (
cos (![]() + α) = - cos (
+ α) = - cos (![]() - α) = - sin α
- α) = - sin α
Р О К
мал. 2
 Кутам π – α і α також відповідають точки одиничного кола, симетричні відносно осі у. Тому
Кутам π – α і α також відповідають точки одиничного кола, симетричні відносно осі у. Тому
sin (π – α) = sin α
cos (π – α) = cos α

![]()
![]()
 Кутам π + α і α (а також
Кутам π + α і α (а також ![]() - α і
- α і ![]() - α,
- α, ![]() + α і
+ α і ![]() + α) відповідають точки одиничного кола, симетричні відносно початку координат (мал. 3).
+ α) відповідають точки одиничного кола, симетричні відносно початку координат (мал. 3).
у Їх ординати протилежні і абсциси
протилежні. Тому
![]() А
А
![]()
 Р α
Р α
![]()
![]() α О К х sin (π + α) = -sin α cos (π + α) = -cos α
α О К х sin (π + α) = -sin α cos (π + α) = -cos α
Д sin(![]() - α) = -sin(
- α) = -sin(![]() - α) = -cos α
- α) = -cos α
cos(![]() - α) = -cos (
- α) = -cos (![]() - α) = -sin α
- α) = -sin α
sin(![]() + α) = -sin(
+ α) = -sin(![]() + α) = -cos α
+ α) = -cos α
 cos(
cos(![]() + α) = -cos (
+ α) = -cos (![]() + α) = sin α
+ α) = sin α
Кутам 2π + α і α відповідає одна й та сама точка одиничного кута, тому

sin(2π + α) = sin α
cos(2π + α) = cos α
Кутам 2π - α і α відповідають точки одиничного кола, симетричні відносно осі х. Їх абсциси рівні, а ординати протилежні. Тому
![]() sin(2π - α) = -sin α
sin(2π - α) = -sin α
cos(2π - α) = cos α
З попередніх міркувань маємо 16 формул. Ще 16 подібних формул можна довести для тангенса і котангенса:
tg(![]() - α) =
- α) = 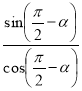 =
= ![]() = ctg α
= ctg α
сtg(![]() - α) =
- α) = 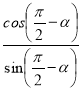 =
= ![]() = tg α.
= tg α.
Отже, tg(![]() - α) = ctg α
- α) = ctg α
сtg(![]() - α) = tg α і т. п.
- α) = tg α і т. п.
Усі ці 32 формули називають формулами зведення, бо вони дають можливість кожну тригонометричну функцію довільного кута звести до тригонометричної функції гострого кута. Запам’ятовувати кожну з цих формул немає потреби, краще користуватись загальним правилом.
Щоб зрозуміліше сформулювати правило, домовимось синус вважати кофункцією косинуса і навпаки, а тангенс – кофункцією котангенса і навпаки. Говоритимемо також, що кут зводжуваної функції відкладається від горизонтального діаметра, якщо він має вигляд π ± α або 2π ± α, чи від вертикального діаметра, якщо він має вигляд ![]() ± α або
± α або ![]() ± α.
± α.
Правило зведення можна сформулювати так:
Якщо кут зводжуваної тригонометричної функції відкладається від вертикального діаметра, то її замінюють кофункцією, якщо ж – від горизонтального діаметра, то її назву не змінюють. Знак ставимо такий, який має значення зводжуваної функції за умови, що кут α гострий.
Приклад. Нехай треба спростити вираз cos(![]() - α). Перед результатом треба поставити знак мінус, бо коли кут α гострий, то кут
- α). Перед результатом треба поставити знак мінус, бо коли кут α гострий, то кут ![]() - α належить третій чверті і його косинус від’ємний. Кут
- α належить третій чверті і його косинус від’ємний. Кут ![]() - α відкладається від вертикального діаметра, тому назву функції cos треба змінити на sin. Отже,
- α відкладається від вертикального діаметра, тому назву функції cos треба змінити на sin. Отже,
cos(![]() - α) = -sin α
- α) = -sin α
До формул зведення можна віднести також тотожності:

cos(-α) = cos α
sin(-α) = -sin α
tg(-α) = - tg α
сtg(-α) = -сtg α
Виконання вправ
1. Знайдемо значення sіn ![]() .
.
Маємо: 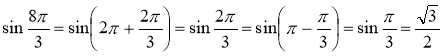 .
.
2. Приведіть до тригонометричних функцій числа а:
а)![]() ; б)
; б)![]() ; в) сtg (π – α); г) tg (π + α); д) sіn (π + α); є)
; в) сtg (π – α); г) tg (π + α); д) sіn (π + α); є)![]() .
.
Відповідь: а) соs α; б) - sіn α; в) - ctgα; г) tg α; д) - sіn α; є) сtg α.
3. Знайдіть:
а) sіn ![]() ; б) соs
; б) соs ![]() ; в) tg
; в) tg ![]() ; г) sіn
; г) sіn ![]() .
.
Відповідь: а) ![]() ; б) -
; б) - ![]() ; в) -
; в) - ![]() ; г)
; г) ![]() .
.
4. Спростіть:
а) 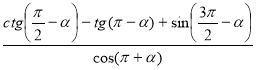 ; б)
; б) 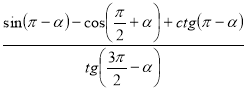 .
.
Відповідь: а) 1. б) –1.
5. Доведіть, що
а) 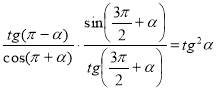 , б)
, б) 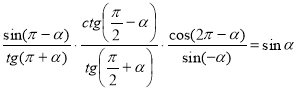 .
.
V. Підведення підсумків заняття.
1. Що таке формули зведення?
2. Які знаки мають тригонометричні функції в кожній із четвертей?
VI. Домашнє завдання.
1. Спростіть вираз:
а) cos (180° - α) б) tg(270° - α) в) cos α + cos(-α)
2. Доведіть тотожність:
sin(α - π) = sin(α + π)
3) Знайдіть значення виразу:
а) sin 300° б) cos 240° в) tg 225°


про публікацію авторської розробки
Додати розробку
