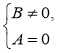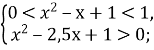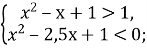Гурток "Заняття математечного гуртока"

Заняття 1

1. Ознайомлення студентів із планом роботи гуртка на 2015 – 2016 н. р.

Затвердження плану роботи гуртка.

2. «Функції навколо нас» (повідомлення керівника гуртка).

3. Методи розв’язування дробово-раціональних рівнянь

 

Хід заняття

 

1. Ознайомлення студентів із планом роботи гуртка на 2015 – 2016 н. р. Затвердження плану роботи гуртка.

 

МЕТА: ознайомити студентів з планом роботи гуртка на 2015 – 2016 н.р., обговорити цей план, внести корективи.

 

2. «Функції навколо нас»

МЕТА: розширити у студентів поняття функції, графіка функції; показати застосування функцій у природі, техніці, побуті. (презентація)

 

3. Методи розв’язування дробово-раціональних рівнянь

МЕТА: домогтися засвоєння студентами змісту понять: «раціональне рівняння», «дробово-раціональне рівняння» – та усвідомлення логічного зв'язку між цими поняттями; сформувати в студентів уявлення про зміст поняття «ОДЗ рівняння», роль його в побудові загальної схеми розв'язання дробово-раціонального рівняння та про саму схему розв'язання дробово-раціонального рівняння; сформувати вміння відрізняти вивчені види рівнянь одне від одного та аргументувати свою думку; знаходити, використовуючи зміст поняття, ОДЗ рівняння, а також розв'язувати найпростіші дробово-раціональні рівняння за вивченою схемою.

 

Раціональні рівняння
1.	Раціональні вирази					Раціональні рівняння
		Цілі вирази	Дробові ви рази				Цілі рівняння = 2	Дробові рівняння = 2
2. Дробово-раціональне рівняння. ОДЗ: значення змінної, при яких існують вирази в обох частинах рівняння.
3. Алгоритм розв'язання рівнянь виду = 0 (А і В — многочлен від однієї змінної). = 0. 1) В ≠ 0 (знайти ОДЗ рівняння): 2) А = 0 (знайти, при яких значеннях змінної чисельник дорівнює нулю); 3) (знайти, які з коренів рівняння А = 0 задовольняють ОДЗ рівняння); 4) Відповідь. (Запишіть у відповідь ці корені)

 

Виконання усних вправ

1.                Які з рівнянь: 2х – 1 = 0; х² – 3х + 5 = 0; 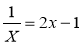; ; 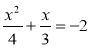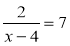є раціональними? цілими раціональними? дробово-раціональними?
2.                Прокоментуйте (використовуючи алгоритм) розв'язання рівняння .

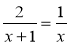1) ОДЗ: х ≠ 0 та х + 1 ≠ 0; х ≠ 0 та х ≠ -1;

2) , , ;

3) х – 1 = 0,

    х = 1 — входить до ОДЗ.

Відповідь. 1.

Виконання письмових вправ

Для реалізації дидактичної мети заняття слід розв'язати завдання такого змісту:

1*. Знаходження ОДЗ дробово-раціонального рівняння виду = 0, де А і В — деякі многочлени від однієї змінної.

2. Перевірка за відомим ОДЗ рівняння, які із заданих чисел не є коре­нями рівняння (не входять до ОДЗ).

3. Розв'язування дробово-раціональних рівнянь виду = 0 (де А і В — деякі многочлени від однієї змінної) за алгоритмом (див. вище).

1) Розв'яжіть рівняння: а) ; б) ; в) .

2) Розв'яжіть рівняння: а) ; б) ; в) .

3) Розв'яжіть рівняння: а) ; б) ; в) .

4. Складання та розв'язування рівнянь за словесним описом.

1) Яке число треба додати до знаменника дробу , щоб дістати дріб ?

2) Яке одне й те саме число треба додати до чисельника дробу і помножити на нього знаменник цього дробу, щоб дістати дріб ?

5. Складання та розв'язування рівнянь за умовою задачі.

Знаменник дробу на 3 більший від чисельника. Якщо до чисельника дробу додати 32, то дістанемо дріб, удвічі більший від даного. Знайдіть початковий дріб.

6. На повторення: перетворити раціональний вираз із використанням набутих раніше знань на заняттях з математики.

Спростіть вираз:

а) 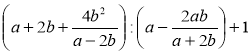;        б) ;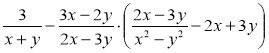

в) ;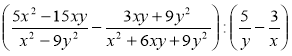

г) .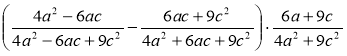

Заняття 2

Відкрите заняття математичного гуртка Інтелект-шоу «Еврика». Між студентами 2-го курсу

 

Хід заняття

 

Інтелент-шоу «Ерудит» – це змагання між студентами 2 курсу групи В спеціальностей «Сестринська справа» та «Лікувальна справа»

 

Мета: розвивати творчі здібності студентів; поглиблювати знання та інтерес студентів до математики, біології та фізики; спонукати студентів до знаходження історичного матеріалу; утверджувати перевагу здорового способу життя над шкідливими звичками.

 

Обладнання: таблиці для роботи журі; дипломи для команди-переможців та медалі , що займе II місце; музичний супровід; мультимедійна презентація.

 

(Звучить тиха спокійна музика)

 

Хід проведення

Ведучий 1

Єдина річ, яка цінується найбільше

Лише тоді, коли немає вже її,

І гірше втрати ти не знайдеш іншого -

Здоров’я найцінніше на Землі!

Ведучий 2

Про здоров’я існує багато мудрих думок і висловлювань. Адже здоров’я людини - найвища цінність. За визначенням ВООЗ, “здоров’я – це не тільки відсутність хвороби, але й стан фізичного, психічного та соціального благополуччя”. Від яких факторів залежить здоров’я? Як відомо, на здоров’я мають вплив:

Ведучий 1

Спадковість -  20%

Ведучий 2

Рівень медицини - 10%

Ведучий 1

Екологія - 20%

Ведучий 2

Спосіб життя - 50%

Ведучий 1

Отже, здоров’я – це той чинник, що залежить переважно від самої людини! Наше здоров’я у наших руках!

Ведучий 2

Сьогодні ми проведемо відкрите засідання математичного гуртка, девіз якого ”Mens mathematikus corpore sano”, що означає ”Математичний розум у здоровому тілі”.

Ведучий 1

Здоров'я - це ранок зі свіжим повітрям,

Це сонце, що гріє ласкаво й привітно,

Це хвилі Дніпра, що нам сили дають.

Бери це сміливо, мій друже, і в путь.

Ведучий2

Та тільки на цьому шляху пам’ятай:

Цурайся цигарки, від чарки тікай.

І знай, любий друже. У цьому житті

Чи бути здоровим – вирішуєш ти.

Ведучий1

Ми зібралися в цьому залі, щоб провести інтелект-шоу «Ерудит» між членами математичного гуртка та знавцями біології і фізики.

Ведучий 2

Для проведення цього заходу запрошуємо дві команди. Перша команда назву  “ХОМО”. Зустрічайте їх.

 

Девіз: Наш девіз завжди такий - більше діла менше слів

             Наш девіз хай знає кожний - Хомо Сапіенс непереможні.

 

Пісня-привітання

Подивись навкруги що з природою стало

Звірі, риби, птахи в невимовній печалі

Може десь у лісах ще щебече пташина

А у нас просто жах, сум мелодії лине

В рідному лісі кожну пташку я знаю

Розв'язання шукаю всіх його проблем

Зорі ранкові його ранки чудові збережем для нащадків збережем.

 

Ведучий 1. Друга команда - “Х, У ТА ДРУЗІ”. Привітаємо учасників гри.

 

Девіз:Мы Х, У и друзья, вместе как одна семья

            Здесь собрались мы, теперь распахнет удача дверь.

 

Вішр-привітання: «Математика моя»

Плюсик ты мой, я – твой минус,

Косинус ты, я – твой синус,

Ты аксиома, я – теорема,

Следствие ты, а я лемма.

Знание ты, я – шпаргалка,

Если ты нуль, то я – палка.

Ты ордината, то я – абсцисса, 

Ты уголок, я – биссектриса.

Ма-те-ма-ти-ка моя…

Я ночами плохо сплю,

Математику я люблю,

Математику я давно, давно люблю.

Я и днем теперь не сплю, я и вечером не сплю,

Все учу, учу, учу, учу, учу.

Частное ты, я – делитель,

Ты знаменатель, я – числитель.

Ты мой кружок, я – твой сектор, 

Ты модуль мой, я – твой вектор.

Сумма моя, а я – разность,

Дольная ты, а я – кратность,

Гипотенуза ты, я – твой катет,

Терминов нам с тобою хватит.

Ма- те-ма-ти-ка моя.

 

Ведучий2.

Щоб це змагання було чесним,

Ми оберемо журі почесне.

Поглянемо разом з вами, друзі,

Хто буде в цім почеснім крузі .     

                                       ( Представлення  членів  журі.)

 

Ведучий 1.

Шановні уболівальники!

Хто уважний, чемний буде -

Бал команді той здобуде.

А як буде пустувати –

Бал команді буде знятий.

Ведучий 2.

Святковий цей зал хай вас всіх поєднає,

В змаганнях він нині ареною стане.

Ведучий 1

Сьогодні ми побачимо – хто швидший і спритніший,

А також всі дізнаємось, хто тут найрозумніший!

Ведучий 2

Нехай обом командам удача посміхається

Учасникам команд та їх уболівальникам бажаємо: “Ні пуху, ні пера!”

Ведучий 1

Повторимо разом: “Ні пуху, ні пера!” (весь зал)

 

Ведучий 2

Але перш ніж перейти до першого конкурсу визначимо, яка команда почне першою наше змагання.

Ведучий 1.

Для цього командам треба відгадати загадку, і яка команда відгадає першою і дасть більш точну відповідь – розпочне змагання.

Ведучий 2.

Отже, загадка: «Скільки часу це тривало?

Не багато і не мало.

По одинадцять тижнів

Було тринадцять раз.

Про що тут йдеться?

Хто відповідь надасть?

Як ви думаєте, що в чорній скринці?

(Книга 1001 ніч», 7*11*13=1001)

Ведучий 1.

У вас є хвилина. Час пішов.

Ведучий 2.

Ось і конкурс перший – «Розминкою» він зветься. Кожній команді по шість питань дається.

Ведучий 1

Правильна відповідь оцінюється 1 балом. За підказки уболівальників 1 бал віднімається. Якщо правильними будуть усі відповіді – команда отримає додатковий бал.

Ведучий 2.

А з якого предмету? З біології, фізики чи математики?

Ведучий 1.

А це кожна команда визначає сама. На екрані перед вами три кнопки, кожна команда обирає будь-яку і відповідно вибирає предмет при цьому.

 

Ведучий 2.

І так як загадку відгадала команда «__________», то цій команді і надається право першій обрати предмет.

(Ведучі по черзі зачитують питання)

І. БІОЛОГІЯ

1. Що в перекладі означає «золото»? (Ранкова зоря)
2. Який птах може нерухомо висіти в повітрі й навіть літати у зворотному напрямку? (Колібрі)
3. Назвіть найбільшу залозу людського організму. (Печінка)
4. Хто дав назву « молочним  зубам»? (Гіппократ)
5. Органи нюху річкового рака. (Короткі вусики)
6. Яка кислота роз’їдає скло? (HF)

 

ІІ. МАТЕМАТИКА

1. Як називається перпендикуляр, опущений з вершини кута на сторону? (Висота)
2. Відстань від точки кола до її центра? (Радіус)
3. У семи братів по одній сестричці. Скільки дітей у сім’ї? (Восьмеро)
4. Яку геометричну фігуру вивчає покарана дитина? (Кут)
5. Двоє учнів йшли до школи і назустріч їм по дорозі ще 5 учнів. Скільки учнів прийшло до школи? (Двоє)
6. Автор підручника з математики, за яким ви навчаєтесь? (Бевз)

 

ІІІ. ФІЗИКА

1. Два види механічної енергії. (Потенційна і кінетична)
2. Англійський вчений, який відкрив основні закони руху тіла. (Ньютон)
3. Коли швидше висихає білизна: в морозну погоду чи у відлигу? (У морозну погоду)
4. Куля, заповнена повітрям, яку використовують для гри. (М'яч)
5. Тривалість одного оберту земної кулі. (Доба)
6. Лінзи в оправі для корекції зору. (Окуляри)

Ведучий 1.

Наступний конкурс називається «Пантоніма». Від кожної команди потрібно по одному учаснику, який добре володіє жестами.

Ведучий 2.

Учасник команди слухає пісню, а потім жестами повинен показати назву пісні. Члени команди повинні сказати назву і виконавця даної пісні.

Ведучий 1.

За відгадану пісню команда отримує – 2 бали. На кожну пісню по 1 хвилині.

 

Ведучий 2

Наступний конкурс «Музичний». Команди оберіть будь ласка цифри. Першою обирає команда «_________»

1.              Фізика
2.              Біологія
3.              Математика

Ведучий 1.

Вам треба написати слова з відповідного предмету, які містять ноти: до, ре, мі, фа, соль, ля, сі. На виконання завдання дається 3 хвилини.

Ведучий 2

Поки команди готуються дорогі вболівальники ми повідгадуєм загадки з біології.

Ведучий 1.

За правильну відповідь команди отримують по 1 балу. Якщо вболівальники однієї команди не знають відповіді, право на відповідь надається вболівальникам іншої команди, якщо відповідь правильна бал зараховується.

(Ведучі по черзі зачитують загадки вболівальникам кожної команди)

1. Не їжак, а має голки, не кенгуру, а має сумку, не курка, а несе яйця. (Єхидна)
2. Якого хижака іноді називають «собакою з головою кішки»? (Гепарда)
3. У якого птаха лише два пальці? (У страуса)
4. Емблема служби переливання крові. (Пелікан)
5. У кого є кисті, але немає рук?  (У винограду, у горобини)
6.  У кого є ребра, але немає хребта? (У куба, призми, піраміди)
7. У кого є кісточки, але немає скелета? (У абрикоса, вишні, сливи тощо)
8. Які нігтики не дряпаються і не знають манікюру? (Квіти нагідки, інакше - календула)
9. Чиї очі різнобарвні і ніколи не моргають? (Квіти братки)
10.  У кого немає ні кулаків, ні біцепсів, а будь-силача з ніг звалить? (У сну)
11.  З якої чашки неможливо пити? (З колінної чашечки)
12. Хто без очей, а сльозами плаче? (Хмара, хмара, бурулька, свічка.)
13.  Хто не має ні легенів, ні зябер, а дихає і зітхає? (Тісто)
14. Без крил летить, без ніг біжить, без вогню горить. (Вітер, хмари, сонце).
15.    Я дерево-красень, а звуть мене .... (Ясен)
16. Біле - не сніг,

         Зелене - не луг,

         Кучеряве - не людина. (Береза)

17. У вінку зеленолистім,

          У червоному намисті

          Видивляється у воду

         На свою хорошу вроду. (Калина)

18. Довгі вуха, куций хвіст,

         Невеличкий сам на зріст.

         На городі побував,

         Там капустки пожував.

        Довгі лапки, скік та скік,

         Ми погнались, а він втік. (Заєць)

19. У річці купається,

         В сорочку не вдягається,

          В повітрі літає,

А завжди суха буває (Дика качка)

20.     Всі пани скинули жупани,

А один пан не скинув жупан. (Сосна)

 

Ведучий 1.

Час вийшов. Листочки зі словами передаємо шановному журі, для перевірки правильності слів і підрахунку балів.

Ведучий 2.

І після цього почуємо скільки балів на данному етапі має кожна команда.

(Листочки передаються журі, оголошуються результати)

Ведучий 1.

А наступний конкурс «Конкурс капітанів».

Ведучий 2

Капітани будь ласка на сцену.

Ведучий 1

Капітан, який знає правильну відповідь дзвонить у дзвоник. Для роздумів капітани мають по 1 хвилині. За правильну відповідь отримує два бали.

Ведучий 2

Але якщо відповідь не правильна, право на відповідь має інший капітан і якщо його відповідь правильно, то також отримує два бали.

Ведучий 1

Конкурс 1. На столі стоїть шість склянок. Три з них порожні, а в три налито воду. Зробіть так, щоб порожні і повні склянки чергувалися. Взяти в руки можна тільки одну склянку.                   

                                 

 

 

(Треба перелити воду з другої склянки в п’яту і поставити порожню склянку на місце)

Ведучий 2.

Конкурс 2. Як з трьох нулів зробити два?

(000           два)

Ведучий 1.

Конкурс 3. Капітани отримують конверти з буквами, з яких треба скласти слово, що означає фізичне явище.

(електризація, випромінювання, конденсація)

  Велучий 2.

Конкурс 4. Дати більш точну відповідь на запитання: «Для того щоб комаха не рухалась, недосвідчений натураліст вміщував у морилку з ефіром її передню частину. Проте комаха не присиплялась. Чому?»

(У більшості комах органи дихання й дихальні отвори розміщені в черевці)

Ведучий 1.

Капітани молодці впорались із своїми завданнями без проблем.

Ведучий2.

А далі перевіримо, яка з команд краще рахує і швидше розв’язує задачі.

Ведучий 1.

Отже наступний конкурс «Хто краще рахує і швидше розв’язує задачі».

Ведучий 2.

Команди по черзі обирають цифру. Команда має хвилину для правильної відповіді. Якщо відповідь правильна команда отримує 2 бали.

Ведучий 1. Якщо ж команда не знає відповіді, право на відповідь має інша команда, яка також може отримати 2 бала.

Ведучий 2.

Першою обирає цифру команда «________».

1. Чи може народитися дитина з 1 групою крові у батьків, які мали 2 групу крові і були гетерозиготами?
2. Пояснити, про які механічні явища ідеться у вірші:

Пливли ми радісно гуртом,

Ti парус прямо нагинали,

Ti одностайно ударяли

Об воду веслами.

(М. Рильський)       (Взаємодія тіл)

3. Руде волосся – рецесивна ознака, неруде – домінантна. При яких шлюбах будуть народжуватись діти з імовірністю 100% з рудим волоссям? 50%? 25%?
4. Записати тисячу 8-ма вісімками, використовуючи тільки знак «+» (888+88+8+8+8=1000)
5. Пляшка з пробкою коштує 10 копійок. Пляшка на 8 копійок дорожча, ніж пробка. Скільки коштує пробка?  (1 копійка)
6. Пояснити, про які механічні явища  ідеться у вірші

Уci ми piвнi перед ним —

I cвітлi, й темні, й pyci.

Коли й на місці на однім,

То все одно ми в pyci.

A він спішить, а він летить,

Бо вічності він служить.

Якщо прогавити хоч мить,

То вже не надолужить. Що це?      (Час.)

 

Ведучий 1.

Наступний конкурс «Придумай!». Команди оберіть цифри.

1.              Тригонометрія
2.              Теплопровідність
3.              Гетерозигота

Ведучий 2. Із даного слова скласти нові слова, які є іменниками, використовувати можна тільки букви даного слова.

Ведучий 1.

У вас є 3 хвилин. Час пішов.

Ведучий 2.

А поки команди думають, пограємо з уболівальниками.

Ведучий 1.

Вам треба назвати прислів’я із числівниками.

Ведучий 2.

Вболівальники, які згадали таке прислів’я піднімають руку. За кожне правильне прислів’я вони приносять своїй команді 1 бал.

 

Ведучий 1.

Отже, час закінчився. Листочки передаємо журі для підрахунку загальної кількості балів.

Ведучий 2.

А поки журі підводять підсумки у команд є можливість отримати додатковий один бал. Увага на екран.

Ведучий 1.

Пояснити це зображення, його зміст та який фізик це розробив.

(Тесла. Тут дві фотографії: на одній Тесла просто сидить з книжкою в руках, а на іншому робота трансформаторного пристрою, який випромінює іскри та електричний розряд. Фотограф проявив ці негативи і наклав одне на одне, при цьому отримав, що вчений сидить і читає книжку під іскрами доща. Це авантюра, фотомонтаж.)

 

Ведучий 2. У вас є хвилина. Час пішов.

 

Ведучий 1.

Слово надається журі нашого інтелект-шоу «Ерудит».

Ведучий 2.

Команда «X, Y та друзі» стала переможцем у нас

І цей диплом почесний

Призначаємо для вас!

Ведучий1

Команда «Хомо»

Теж добре працювала

І від переможця

Лиш трішечки відстала.

Тому ви отримуєте медалі.

Ведучий 2

Всі добре працювали

І команди, і вболівальники.

Ведучий 1

На спогад про цю зустріч

Одержуйте «нулі».

Смачні вони й солодкі,

Хоч, правда, і малі.

Ведучий 2

Ми з вами, сподіваємось,

Зустрінемось не раз,

На зустріч приходьте –

Гурток чекає на вас!

Заняття 3

Практичне заняття гуртка.

Виготовлення моделей стереометричних фігур.

 

Хід заняття

 

МЕТА: навчити студентів виготовляти моделі стереометричних фігур: призма, куб, піраміда, конус.

 

                                   

    

Заняття 4

1. «Як людина навчилася лічити?», (повідомлення викладача, демонстрація таблиць).

2. Методи розв’язування раціональних нерівностей.

 

Хід заняття

 

1. «Як людина навчилася лічити?»

МЕТА: ознайомити студентів з тим, як в давнину рахували та робили записи чисел.

 

У своєму житті людина постійно звертається до чисел. Прокидаючись, ми зазвичай згадуємо який сьогодні день, о котрій годині необхідно відправитися в школу, де нас вчать читати, писати, рахувати. Що може бути простіше рахунку?

Говорити поспіль: раз, два, три і т. д. може всякий. Зараз важко уявити собі дорослої людини, що не вміє рахувати.

І все ж був час, коли люди рахувати не вміли. Спочатку люди знали тільки два числа: один і два. Число один вони пов’язували з одиничним предметом, наприклад: місяць, сонце. Число два пов’язувалося з парними предметами (очі, вуха, крила, руки).

Якщо предметів було більше двох, то люди говорили просто багато. Багато було зірок на небі, а й пальців на руці було теж багато.

Пізніше люди навчилися рахувати до п’яти і з’єднувати два п’ятка в десяток. Пальці допомогли навчитися рахувати і виконувати найпростіші дії з числами. Загинав людина пальці — складав, розгинав-вичитав. Для запам’ятовування чисел люди користувалися зарубками на деревах і на палицях, вузлами на мотузках.

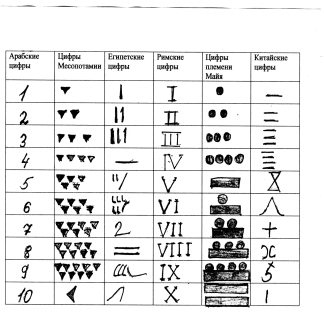
У стародавньому Єгипті кожна річ, кожна дія зображувалися картинкою. Поступово картинки замінили ієрогліфи. Писали стародавні єгиптяни на папірусі. Папіруси, пролежавши в сховищах пірамід близько 40 століть, збереглися до наших днів.

Спеціальних знаків для запису чисел тоді не було. Особливо цікавий спосіб запису чисел виник в стародавньому Вавилоні. Люди писали паличками на плитках з м’якої глини і обпалювали потім свої рукописи. Картинки-ієрогліфи були побудовані з вузьких вертикальних і горизонтальних клинцем. Цю писемність так і називають клинописом.

Одиниця позначалася одним клинцем, два — двома і т. д., до дев’яти клинцем. Числа великі 5 власних назв не мали.

6 називали п’ять і один, 7 — п’ять і два і так далі. Число 10 називали особливим словом і видавлювали у вигляді широкого лежачого клину. Стародавні римляни записували числа рисками. Вчені припускають, що знак для одиниці — це ієрогліф, що зображає один палець, знак для п’ятірки — це спрощене зображення п’яти пальців (кисть руки з відстовбурченою великим пальцем), а десять — це дві складені разом п’ятірні. Цікаво, що у різних народів, в різні часи, були схожі способи запису чисел.

Такі записи дозволяли додавати до записаного числа одиницю простим приписуванням нового знака, а щоб відняти одиницю треба закреслити зайвий значок. Коли з’явилися літери, багато народів стали використовувати алфавіт для позначення чисел. Щоб відрізнити літери від чисел, слов’яни ставили над літерами, які зображували числа, особливий знак, названий титло.

Ця нумерація виявилася з часом незручною, так, як в ній не можна було записувати великі числа. Сучасні, так звані арабські цифри були винайдені в Індії, а в Європу вони були завезені з арабських країн. Записувати цифри таким способом набагато зручніше і швидше.

Вони вживаються в нашій країні з XVII століття. Римські ж цифри досі зустрічаються на циферблатах годинників, вживаються для позначення глав книги, сторіч.

При складанні короткої записи завдань ми теж використовуємо римські цифри. Мова математики не знає національності, тому, що він належить усьому людству.

  

2. Методи розв’язування раціональних нерівностей.

МЕТА: розширити знання студентів про раціональні нерівності; навчити розв’язувати раціональні нерівності методом інтервалів та заміною змунної; навчити розв’язувати раціональні нерівностей вищих степенів узагальненим методом інтервалів.

 

1. Загальні відомості про раціональні нерівності

Дві функції, що поєднані між собою знаю утворюють нерівність:

;

.

Розв’язком цих нерівностей називається значення , що задовольняє їх. Розв’язати нерівність – значить знайти множину всіх її розв’язків або встановити, що нерівність не має розв’язків.

Областю визначення (областю допустимих значень) нерівності називають множину всіх значень невідомого, на якій існують функції . При визначенні часто вводяться також додаткові умови, які пов’язані з характером нерівності.

Під множиною розв’язків системи нерівностей розуміють перетин множин розв’язків всіх нерівностей, що входять в цю систему.

Говорять, що нерівність еквівалентна системі нерівностей, якщо множина її розв’язків співпадає з множиною розв’язків цієї системи.

 

2. Теореми про рівносильність нерівностей

Дві нерівності з одною змінною називаються рівносильними, якщо їх розв’язки співпадають (в тому числі, якщо обидві нерівності не мають розвязків). Якщо кожен частковий розвязок нерівності являється в той же час частковим розвязком нерівності , отримані після перетворення нерівності , то нерівність називається наслідком нерівності . В наступних теоремах річ йде про перетвореннях, які ведуть до рівносильних нерівностей.

Теорема 1. Якщо з однієї частини нерівності перенести до іншої доданок із протилежним знаком, то дістанемо нерівність, рівносильну початковій.

Теорема 2. Якщо до обох частин нерівності додати (або відняти) будь-яку функцію то дістанемо нерівність, рівносильну початковій за умовою, що області визначення отриманої і початкової нерівностей збігаються.

Теорема 3. Якщо обидві частини нерівності помножити (або поділити)на будь-яку функцію , яка зберігає сталий знак і відмінну від нуля, то при дістаємо нерівність, рівносильну початковій, а при рівносильною початковій буде нерівність протилежного змісту (передбачається, що області визначення отриманої і початкової нерівностей збігаються).

Таким чином, можемо записати:

, якщо ;

, якщо ;

, якщо ;

, якщо ;

Зауваження. На практиці при застосуванні 2 і 3 теорем найчастіше замість функції береться її окремий випадок – відмінна від нуля константа.

 

3. Приклади розв’язування раціональних нерівностей вищих степенів різними методими

 

Розвязування раціональних нерівностей вищих степенів методом інтервалів

Будемо розглядати розв’язання раціональних нерівностей методом інтервалів. Існують різні схеми реалізації цього методу. Розглянемо одну з цих схем, допускаючи, що розв’язується нерівність . У випадку нерівності ця схема аналогічна.

1.Перенести всі члени нерівності вліво:

.

2.Ліву частину отриманої нерівності привести до спільного знаменника:

.

3.Багаточлени і розкласти на множники. Якщо при цьому з’являються однакові множники, то треба замінити їх відповідним степенем. Наприклад,

.

При скороченні треба мати на увазі, що:

 

4. Виключити з розкладення нелінійні множники. Це виключення виконується таким чином.

Якщо в розкладенні є множник, , де , то його виключення залежить від знака старшого коефіцієнта і виконується за правилом:

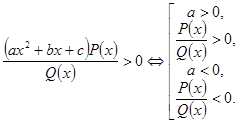
Якщо в розкладенні є множник , то його виключення здійснюється за правилами

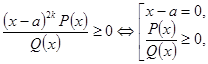
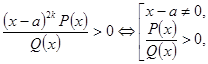
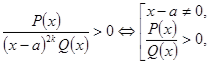
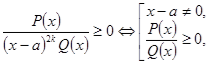
Нелінійний множник виключається за правилом:

.

5. На числовій осі відмітимо точки, в яких обертаються в нуль всі множники, що стоять в чисельнику і знаменнику лівої частини нерівності, отриманої в результаті виконання пунктів «1» - «4». При цьому, якщо нерівність нестрога, точки, які відповідають множникам чисельника будемо визначати зафарбованими кружками, а точки, що відповідають множникам знаменника світлими. Якщо нерівність строга, всі точки відмічаються світлими кружками.

6. Поставити знаки в кожному проміжку, на якій числова вісь розбивається відміченими точками.

Спочатку поставити знак у самому правому проміжку на числовій осі за правилом: знак «+» ставиться, якщо число множників виду парне, і знак «-», якщо це число непарне. Знаки в інших проміжках ставляться з урахуванням того, що вони чергуються в сусідніх проміжках.

7. Вибираються проміжки, в яких стоїть знак «+», якщо нерівність, отримана в пункті 4 має вигляд: , або «-», якщо ця нерівність має вигляд . Ці проміжки містять у собі крайні точки, відмічені на числовій осі зафарбованими кружками, і не містять точок, відмічених світлими кружками,. Об’єднання цих проміжків і є множиною розв’язків даної нерівності.

Приклад 1. Розв’язати методом інтервалів нерівність

. (1)

Розв’язування:З нерівності знаходимо ОДЗ:

Далі замість нерівності (1) розв’язуємо рівняння

або звідки

Наносимо відповідні точки на числову вісь (див. рисунок).

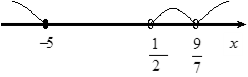
Розглядаємо кожний з утворених інтервалів окремо.

1. Підставляємо значення з інтервалу у нерівність (1). Дістаємо нерівність , яка не виконується. Тому нерівність (1) не виконується в усіх точках інтервалу .

2. Підставляючи в нерівність (1) значення з інтервалу , дістаємо правильну нерівність . Отже, нерівність (1) виконується на інтервалі .

3. Підставляючи в (3) значення з інтервалу дістаємо неправильну нерівність . Це означає, що нерівність (1) не виконується ні в одній точці інтервалу .

Остаточно маємо розв’язок нерівності (1)

Відповідь.

Приклад 2. Розв’язати нерівність

Розв’язування: Для знаходження коренів рівняння необхідно розкласти його на множники. Отже

Отже числа,, є коренями даного рівняння. Наносимо ці числа на числову вісь і визначаємо знак лівої частини функції

на одному з інтервалів. Зокрема, взявши точку з інтервалу , дістаємо . Провівши «криву знаків», визначаємо знак в кожному з інтервалів.

Відповідь:

 

Розв’язування раціональних нерівностей вищих степенів узагальненним методом інтервалів

Нехай потрібно розв'язати нерівність

,

де цілі додатні числа;

— дійсні числа, серед яких немає рівних і такі, що . Нерівності подібного типу розв'язують із застосуванням узагальненого метода інтервалів. В основі цього метода лежить така властивість двочлена точка ділить числову вісь на дві частини, причому якщо (- парне), то вираз праворуч і ліворуч від точки зберігає додатний знак; якщо (- непарне число), то вираз праворуч від точки додатний, а ліворуч від точки від'ємний.

Для розв'язання нерівності

узагальненим методом інтервалів на числову вісь наносимо числа ; в проміжку праворуч від найбільшого з них ставимо знак «плюс», а потім, рухаючись справа наліво, при переході через чергове число змінюємо знак, якщо — непарне число, і зберігаємо знак, якщо. — парне число.

Зауваження 1. Якщо зустрічаються вирази , то праворуч від найбільшого з не обов'язково буде знак « + ». У цьому випадку найкраще визначити знак лівої частини нерівності в якомусь з інтервалів, а потім поставити знаки в кожному з інтервалів з урахуванням викладених вище міркувань.

Зауваження 2. Наведені вище міркування справедливі і для нерівностей виду

, , , де

.

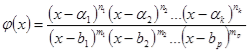Приклад 1. Розв’язати нерівність

Перепишемо нерівність у рівносильному вигляді

Числа , , , є коренями рівняння. Наносимо ці числа на числову вісь і визначаємо знак лівої частини функції

на одному з інтервалів. Зокрема, взявши точку з інтервалу , дістаємо . Проводимо через задані точки «криву знаків» з урахуванням того, що ліворуч і праворуч точки буде той самий знак «+», тому що у виразі показник степеня (число 4) є числом парним.

Відповідь:.

Приклад 2. Розв’язати нерівність

Числа ,, є коренями рівняння. Наносимо ці числа на числову вісь і визначаємо знак лівої частини функції на одному з інтервалів. Зокрема, взявши точку з інтервалу , дістаємо . Провівши «криву знаків» з урахуванням того, що ліворуч і праворуч точки і буде той самий знак «-», тому що у виразах і (х + 3)⁶ показник степеня (число 4 і 6 відповідно) є парні числа, визначаємо знак f(x) в кожному з інтервалів.

Відповідь: .

Приклад 3. Розв’язати нерівність

Числа, , є коренями рівняння Наносимо дані точки на числову вісь. Оскільки дискримінант квадратного тричлена х² , то для всіх і, значить, парабола не перетинає вісь Ох. За допомогою «кривої знаків» дістаємо розв’язання.

Відповідь: .

Приклад 4. Розв’язати нерівність

Числа , , є коренями рівняння Наносимо дані точки на числову вісь і визначаємо знак лівої частини функції на одному з інтервалів. Зокрема, взявши точку з інтервалу , дістаємо . Проводимо через задані точки «криву знаків» і дістаємо розв’язання.

Відповідь:..

 

Приклад 5. Розв’язати нерівність

.

Перепишемо нерівність

.

Числа, , є коренями рівняння Наносимо дані точки на числову вісь і визначаємо знак лівої частини функції

на одному з інтервалів. Зокрема, взявши точку з інтервалу , дістаємо . Проводимо через задані точки «криву знаків» і дістаємо розв’язання.

Відповідь:.

 

Розв’язування дробово-раціональних нерівностей

Приклад 1. Розв’язати нерівність

.

Розв’язання: розкладемо чисельник і знаменник дробу, що стоїть в лівій частині нерівності, на множники:

.

Отриманий дріб містить два нелінійні множники: і . Перший з них додатний і його можна опустити, другий множник виключимо у відповідності з пунктом 4:

Далі, на числовій осі відмітимо точки , та інтервали, що утворюються при цьому, знаками:

Виберемо інтервал відмічений знаком «-» (так як ), і нанесемо на числову вісь точку . Ця точка попадає у вибраний інтервал. «Виколюючи» точку , отримуємо інтервали і , об’єднання яких утворює множину розв’язків даної нерівності:
 

Відповідь: .

Приклад 2 . Розв’язати нерівність

.

Розв’язання: розкладемо багаточлен, що стоїть в чисельнику лівої частини нерівності, на множники. Розглянемо рівняння . Серед дільників 8 підберемо корінь рівняння . Розділимо ліву частину рівняння на двочлен :

 

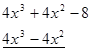
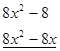
Тепер розглянемо рівняння . Серед дільників 8 підберемо рівняння і розділимо ліву частину на двочлен :

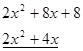
Так як квадратний тричлен не має дійсних коренів, отримаємо розкладення

.

Таким чином, дана нерівність перетворюється до вигляду:

.

Дріб в лівій частині цієї нерівності містить два нелінійних множники: квадратний тричлен , що більший нуля, і . Виключимо ці множники:

 

На числовій осі відмітимо точки , і інтервали, що утворюються знаками:

Виберемо інтервал зі знаком «-» і потім відмітимо на осі точку . Ця точка належить вибраному інтервалу, і тому, виключаючи цю точку, отримуємо, що - множина розв’язків даної нерівності.

Відповідь: .

Приклад 3. Розв’язати нерівність

.

Розв’язання: у відповідності з описаною схемою методу інтервалів

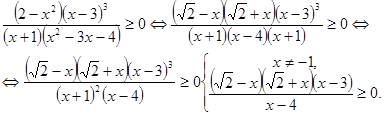
Будемо відмічати на числовій осі точки , , зафарбованими кружками (нерівність нестрога!), а точку - світлим кружком:

 

Розв’язок даної даної нерівності складаються з об’єднанням проміжків .

Відповідь: .

Приклад 4. Розв’язати нерівність

.

Розв’язування: Нанасимо на числову пряму точки , , , , . Точки , , відзначаємо темними кружками, а точки , світлими.

Провівши «кривину знаків» з урахуванням того, що в околі точок і ліва частина нерівності зберігає знак (тому що у виразах ), показники степенів є парними числами), дістанемо розв’язання Ця множина на рисунку заштрихована.

Відповідь:

Приклад 5. Розв’язати нерівність

.

Наносимо точки числову вісь. За допомогою «кривої знаків» дістанемо розв’язки, заштриховані на рисунку.

Зазначимо, що точка входить у множину розв’язків, тому що при дістанемо .

Відповідь: .

 

Розв’язування раціональних нерівностей методом заміни змінної

Приклад 1. Розв’язати нерівність

Зробивши заміну змінної , дістаємо

.

 

Коренями рівняння

є , .

Звідси

.

Оскільки , то дістаємо

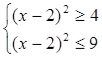
Розв’яжемо нерівність

 

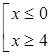
Розв’яжемо нерівність

Розв’язком початкової нерівності є об’єднання множин і .

Відповідь: і

Приклад 2. Розв’язати нерівність

Зробивши заміну змінної , дістаємо

.

Коренями рівняння є , .

Звідси.

Оскільки , то дістаємо

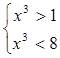
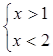
Зобразимо отриману множину за допомогою координатної прямої.

Відповідь: .

 

 

Заняття 5

1. Домашнє завдання: виступи членів гуртка із творами: «Математика і моя майбутня професія», «Чи може людина прожити без математики?»

2. «Геометрія Всесвіту» (розгляд таблиць, фотознімків).

3. Методи розв’язування рівнянь, що містять знак модуля

 

Хід заняття

 

1. Домашнє завдання: виступи членів гуртка із творами: «Математика і моя майбутня професія», «Чи може людина прожити без математики?»

МЕТА:  виховувати у студентів любов до математики, не тільки як до шкільного предмету, а й як до предмету , який потрібен їм у майбутній професії.

(Твори студентів додаються)

 

2. «Геометрія Всесвіту»

МЕТА:  ознайомити студентів з геометрією Всесвіту, з фрактальною та сакральною геометрією.

 

Поняття “фрактальна геометрія” і “фрактал” виникли в кінці 70-х рр.., а з другої половини 80-х вони міцно увійшли в словник програмістів, математиків і навіть фінансових трейдерів . Сам термін “фрактал” походить від латинського “fractus” і перекладається як «що складається з фрагментів». Цим словом в 1975 році американський і французький вчений Бенуа Мандельброт позначив нерегулярні, але самоподібні структури, якими він у той час займався. У 1977 році вийшла його книга, яка була повністю присвячена такому унікальному і красивейшему явищу, як фрактальна геометрія природи.

Сам Бенуа Мандельброт був математиком, однак термін «фрактал» не відноситься до математичних понять. Як правило, під ним розуміють геометричну фігуру, що володіє одним або кількома такими властивостями:

1) при збільшенні у неї виявляється складна структура;

2) в тій чи іншій мірі ця фігура подібна собі самій;

3) її можна побудувати за допомогою рекурсивних процедур;

4) для неї характерна дробова хаусдорфових (фрактальна) розмірність, що перевищує топологічну.

Фрактальна геометрія – це справжня революція в математичному описі природи. З її допомогою можна описати світ набагато зрозуміліше, ніж це робить традиційна математика або фізика. Візьмемо, наприклад, броунівський рух. Здавалося б, у випадковому переміщенні частинок пилу, зважених у воді, панує цілковитий хаос. Проте і тут присутній фрактальна геометрія. Безладне броунівський рух має частотної характеристикою, яку можна використовувати для прогнозування явищ з великим числом статистичних даних. Це не може не викликати здивування. Однак саме броунівський рух допомогло у свій час Мандельброту передбачити цінові коливання вартості вовни.

Фрактальна геометрія знайшла широке застосування в комп’ютерній техніці. От уявіть собі, що потрібно скласти програму, яка зможе вивести на екран тривимірну модель берегової лінії, гір або узлісся. Якими формулами все це можливо описати? Якими функціями скористатися? І тут на допомогу приходять фрактали. Подивіться на маленьку гілочку – це крихітне подобу великого дерева. Маленьке хмарка являє собою щось на зразок великої хмари, а молекула – крихітний аналог галактики. Так, застосовуючи рекурентні формули, тобто ті, які посилаються самі на себе, можна моделювати цілком реалістичні зображення.

Фрактальна геометрія знаходить своє застосування в архітектурі, образотворчому мистецтві (фрактальний імпресіонізм). Гучні свого часу картини Джексона Поллака є яскравим тому прикладом. За допомогою фракталів індустрія кіно здійснила справжній прорив – до цього штучні елементи ландшафту ніколи ще не виглядали настільки реалістично. Економісти використовують їх для прогнозування коливань курсів паперів. Світ фракталів зберігає ще багато дивного, адже це жива мова природи

 

Сакра́льна геоме́трія (від лат. Sacralis — священний, що володіє святістю, визнаний божественним) — сукупність релігійних та/або міфологічних уявлень про форми і простір світу, його гармонії, впорядкованості, пропорційності, як геометрія форм, що лежать в основі життя.

Сакральна геометрія — частина міфологічного і релігійного світогляду, результат містичного досвіду. Сакральна геометрія застосовувалася у всі часи і у всіх світових релігіях, в музиці, мистецтві, в архітектурі храмів і вівтарів, в живописі та іконографії — як божественна пропорційність, в геометричній інтерпретації космосу — як форми впорядкованості Всесвіту (на противагу хаосу).

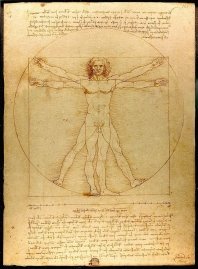Найбільш значуща сакральна геометрична фігура древніх єгиптян це анкх☥ (анк, анх) — символ життя в Стародавньому Єгипті. У ньому укладені дві фігури: хрест як символ життя і коло як символ вічності. Всі разом розуміється як безсмертя або «майбутня життя». Іноді цю форму представляють як сонце, що сходить, як єдність протилежностей, як чоловіче і жіноче начало. Анх представляють і як магічний символ мудрості. Його можна знайти в багатьох зображеннях божеств і священнослужителів часів єгипетських фараонів. Багато єгипетські боги зображувалися з анхом в руці. Припускають, що Анх являє собою одну з форм Древа Життя. Овал означає вічність або кругообіг життя, а хрестоподібному розширення, розуміється як перехід з нескінченності в простір. Малюнки богів теж являють собою геометричні форми, але складніші. Для відтворення малюнків, в живописі, необхідно знати геометрію, математику, враховувати пропорції, як це показано в роботі Вітрувіанська людина Леонардо да Вінчі.

Найважливішим для християнства є геометрична форма хреста, один з найдавніших сакральних символів. Існує велика різноманітність форм і розмірів, наприклад, мальтійський хрест, Кельтський хрест — символ давнього кельтського християнства. Вважають, що він має давніші язичницькі корені. Існують численні приклади зображення хреста і кола, які деякі джерела називають «сонячними хрестами».

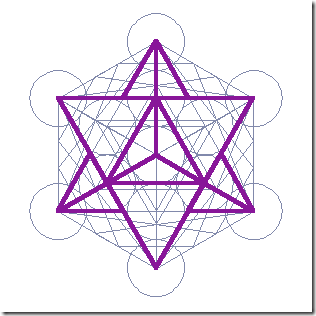
Іншою досить важливою фігурою сакральної геометрії християнства можна вважати зірку. Один з варіантів цієї фігури ✡ можна зустріти в Старому Завіті.

 Вважається, що цей знак відображений у печатці Соломона, отриманої від батька (зірка Давида). За іншою версією, печатка Соломона, це восьмикінечна зірка, у вигляді пентаграми ۞. Ця сакральна восьмикутна геометрична фігура, яка зображується на одязі священиків, на деяких іконах (Неопалима Купина), у вигляді духовних відзнак, орденів і амулетів. Сакральна геометрія Зірки Віфлеєму має чотирнадцять променів.

Фрактальна геометрія                                         Сакральна геометрія

           

     

  

 

 

3. Методи розв’язування рівнянь, що містять знак модуля

МЕТА:  узагальнити та систематизувати знання студентів про модуль числа, алгебраїчний та геометричний зміст модуля; формувати вміння і навички розв’язування лінійних рівнянь, що містять модуль.

 

Абсолютною величиною невід’ємного дійсного числа називається саме це число, а абсолютною величиною від’ємного числа називається протилежне додатне йому число.

 Із даного означення виходить, що модуль дійсного числа – число невід’ємне. Абсолютну величину дійсного числа можна визначити через арифметичний квадратний корінь із .

Геометричний зміст модуля.

Модуль дійсного числа має просте геометричне тлумачення:

Довжина відрізка ОА, якщо а>0; точка О, якщо а=0; довжина відрізка ОВ, якщо а<0; тобто АО=ВО=

Властивості модулів дійсних чисел а і b:

1.     ;
2.     ;
3.     ;
4.     ;
5.     ;
6.     ;
7.                   .
8.                    

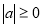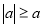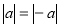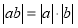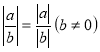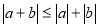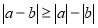1.Розв’язування  лінійних  рівнянь з модулями. 

а)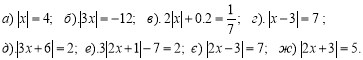

2.Розвязати рівняння:

    .

Розв’язання:

     , якщо  а=b  або  а=-b.

Відповідь: 4;-0.4.

Відповідь:; 2.

Відповідь: -2;2.

 

 

 

 

Відповідь:-2;2.

 

ІІ. Розв’язування рівнянь за  загальною  схемою.

Алгоритм:

1. Знайти нулі всіх підмодульних виразів і позначити їх на ОДЗ рівняння.

2. На кожному з одержаних проміжків розкрити модулі і записати рівняння без знака модуля.

3. Розв’язати отримане рівняння без модулів.

4. Записати відповідь з урахуванням проміжку, що розглядається.

1. Розв’язати рівняння:  .

Розв’язання:

 

     3-х=0, х+2=0;

     х=3  х=-2

 

1. 
   x<-2;   

   3-х+х+2=5,

 5=5,

   х є (-; -2).

 

2. -2;

3-х-(х+2)=5,

3-х-х-2=5,

-2х=4,

х=-2, -2 є .

 

3. х>3; 

-(3-х)-(х+2)=5,

-3+х-х-2=5,

-5=5, невірно.     

Немає розв’язків.

Відповідь: (-;-2].

 

2. |x+3|+|2x-1|=8

Розв’язання:

|x+3|+|2x-1|=8

х+3=0;  2х-1=0;

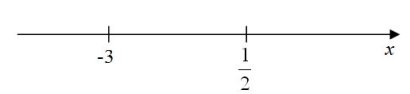
        х=-3            х=.

1) х<-3;

    -(x+3)-(2x+1)=8,

    -x-3-2x+1=8,

    -3x=10,

    x=; 3 є (-; -3).

 

2) -3; 

   х+3-2х+1=8,

   х=-4; -4 [-3; ];

 

3) x>;

    x+3+2x-1=8,

    3x=6,

    x=2,      2 є (; +).

Відповідь:  -3; 2.

 

3. |5-x|=2∙|2x-5|

Розв’язання:

|5-x|-2|2x-5|=0

5-x=0,     2x-5=0,

x=5 ,        x=2,5.

1) x<2,5;

 5-x+2|2x-5|=0,

 5-x+4x-10=0,

     3x= 5,

      x=,

      x=    є (-; 2,5).

 

2) 2,5;

     5-х-4х+10=0,

        -5х=-15,

          х=3,     3 є [2,5; 5]

 

3) х>5;

    -5+x-4x+10=0,

    -3x=-5,

    x=,    (5; +).

 Відповідь: ; 3.

4. |x-3|+|2x-1|+|x+7|=-2

Розв’язання:

Рівняння немає дійсних коренів, оскільки сума додатних чисел не може дорівнювати від’ємному числу.

Відповідь: Немає розв’язків.

 

5. |x+2|+|2x-3|+|x-1|+|x-3|-3x+12=0.

Розв’язання:

Запишемо рівняння у вигляді:

|x+2|+|2x-3|+|x-1|+|x-3|=3x-12.

Ліва частина рівняння додатна. Отже, рівняння може мати дійсні корені, якщо 3х-120, тобто при х4. А на цьому проміжку вирази, записані в кожному з модулів, додатні. Рівняння рівносильне системі:

 

немає розв’язків.

Відповідь: Немає розв’язків.

 

6.

Розв’язання:

;

х²-9=0,    х²-4=0,

(х-3)^.(х+3)=0,  (х-2)^.(х+2)=0, 

х=-3 або х=3;  х=-2 або  х=2

1) х;    2)-3 ;

х²-9+х²-4=5,      -х² + 9 +  х²- 4 = 5,

   2х²=18,             5 = 5,

   х²=9,                х  є  [-3; -2]

х =-3; х =3.

-3

3 . Немає розв’язку.

3) -2;                               4) 2;                 

     -х²+9-х²+4=5,      -х²+9+х²-4 =5, 

     -2х²  = -8,          5=5, 

         х² = 4,               х  є  (2; 3]; 

     х₁ = 2;  х₂ = -2.              

     х є  (-2; 2];   

 

 

5) х3;

    х²-9+х²-4=5,

    2х²=18,

    х²=9,

   х₁=-3, х=3.

Немає розв’язку.   

Відповідь:      

 

 

 

 

Заняття 6

1. Підбір матеріалів для випуску математичної газети.

2.Підготовка до олімпіади. Розв’язування олімпіадних завдань

3. «Розвивайте свою пам‘ять», «Чи вмієте ви рахувати» (виступи членів гуртка із рефератами).

 

Хід заняття

 

1. Підбір матеріалів для випуску математичної газети.

МЕТА:  розвивати у студентів творчі здібності, виховувати любов до математики.

 

2.Підготовка до олімпіади. Розв’язування олімпіадних завдань

МЕТА: вчити студентів розв’язувати олімпіадні завдання, евристичні задачі; розвивати логічне мислення.

(Олімпіадні завдання минулих років додаються)

1. Розв’язати нерівність

Розв’язання

1. 

         , бо

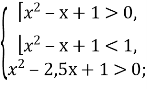
2)

х=0, х=1

3)

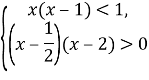
Наносимо розв’язки на числову пряму і вказуємо проміжки, які задовольняють, отримуємо .

2. 

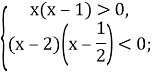
Наносимо розв’язки на числову пряму і вказуємо проміжки, які задовольняють, отримуємо

Відповідь: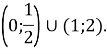

2.Побудуйте графік функції

 .

Розв’язання

При

При     .

3. Обчисліть

Розв’язання

Так як буде .

 

4. Розв’яжіть систему рівнянь

 

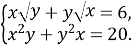
Розв’язання

Піднесемо обидві частини першого рівняння системи до квадрату:

 

Далі замість , підставимо число 20. Так як бачимо, що це друге рівняння нашої системи. Тоді маємо

або

тобто

Це рівняння і друге рівняння заданої системи утворюють систему

              або     

 

Розв’язавши маємо пари розв’язків (4;1) і (1;4). Зробивши перевірку, маємо, що розв’язки задовольняють дану систему.

 

3. «Розвивайте свою пам‘ять», «Чи вмієте ви рахувати»

МЕТА: формування в студентів вміння виступати перед публікою; виховувати любов до математики; розвивати пам’ять студентів, привчати до самостійного рахування без калькураторів.

(Реферати додаються)

Заняття 7

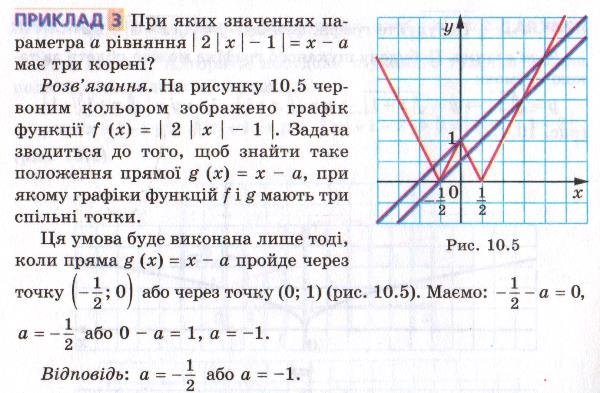
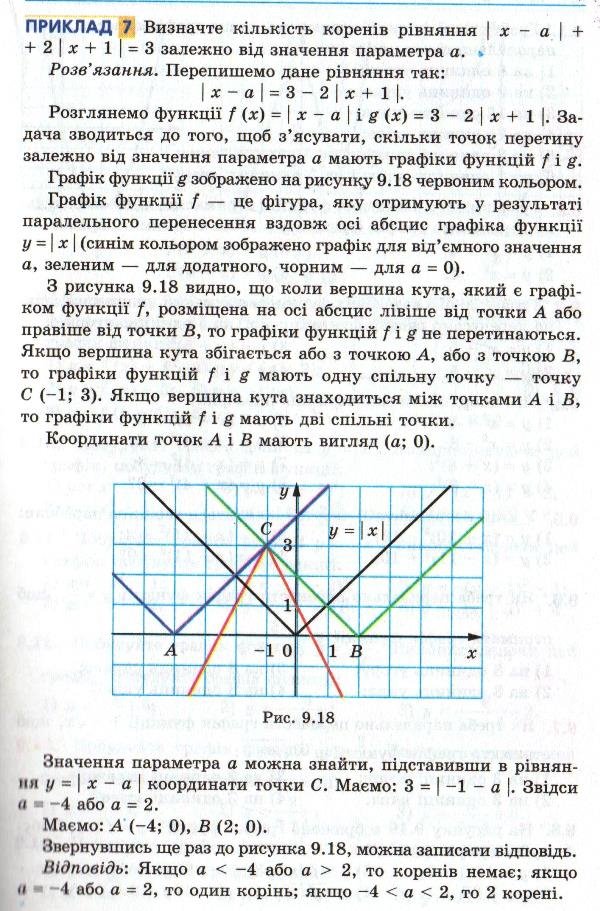
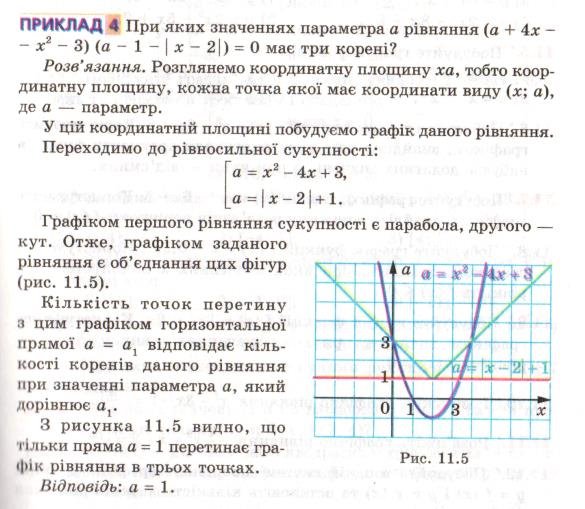
1. Методи розв’язування рівнянь з параметром. (повідомлення викладача).

2.Конкурс художників – математиків.

 

Хід заняття

 

1. Методи розв’язування рівнянь з параметром

МЕТА: формування у студентів розв’язування більш складних лінійних та квадратних рівнянь з параметрами; формування вміння розв’язувати рівняння графічним методом.

 

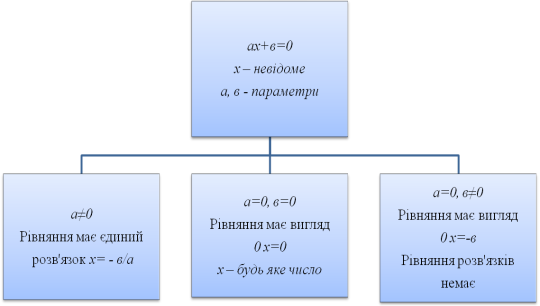
Методи розв’язування лінійних рівнянь з параметрами

 

 

 

 

 

 

 

1. При якому значення параметра в рівняння 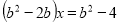має безліч розв’язків? (В. ).
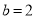2. При якому значення параметра з рівняння 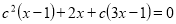має безліч розв’язків? (В. )
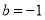3. При якому значенні параметра а рівняння 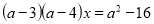не має розв’язку? (В. )
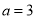4. Визначити при яких значеннях 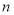рівняння 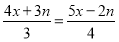має додатні розв’язки. (В. )
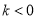5. При якому значенні параметрів 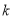рівняння 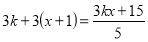не має розв’язку? ()
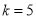6. Визначити при яких значеннях параметра а корні рівняння 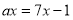кратні 5. (В. )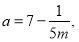
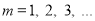7. Розв’язати рівняння

де а — параметр.

(В. якщо то

то

то

то

то

8. При яких значеннях параметра а всі розв’язки рівняння 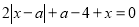задовольняє нерівність 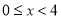? (В.
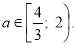
9. При яких значеннях параметра а рівняння 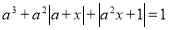має не менше чотирьох цілих коренів? (В.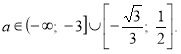
10.               При яких значеннях параметра а рівняння

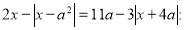
а) не має розв’язків;

б) має кінцеву непорожню множину розв’язків?

 

Розв'язування квадратного рівняння з параметром  треба розпочинати з питання «А чи є воно квадратним?». Дійсно, якщо коефіцієнт перед х² може приймати нульове значення, то наше рівняння може перетворитись на лінійне. А якщо коефіцієнт перед х² не нуль , то наявність розв’язків та їхня кількість залежить від значення дискримінанту рівняння.

 Розв'язування квадратного рівняння можна представити у вигляді схеми:

 

 

 

 

 

 

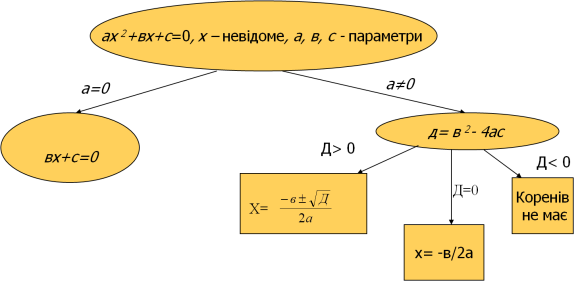
1. Знайти всі значення параметра а, при кожного з яких рівняння

має два різні від’ємні корені. (В. ).

2. Знайти всі значення при яких сума коренів рівняння дорівнює сумі квадратів його коренів. (В. )

3. Знайти кількість цілих значень параметра при яких добуток коренів рівняння належить проміжку ?

4. У рівнянні визначити , при якому відношення коренів цього рівняння дорівнює (В. )

5. При яких значеннях корені рівняння належать інтервалу ?

6. При яких значеннях корені квадратного рівняння мають різні знаки? (В.

7. Знайти найбільше значення параметра при якому рівняння не має двох різних дійсних розв’язків. (В. )

8. При якому найменшому цілому значенні параметра корені рівняння знаходяться по різні боки проміжку ? (В. )

9. Розв’язати рівняння:

(В. )

10. Розв’язати рівняння:

Якщо , якщо .

Графічне розв’язання рівнянь з параметрами

Алгоритм графічного методу:

1. Знайти область допустимих значень невідомого та параметрів, що входять до рівняння.
2. Виразити параметр як функцію від невідомого: .
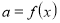3. В системі координат 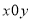побудувати графік функції 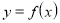для тих значень х, які входять в область визначення рівняння.
4. Знайти точки перетину прямої 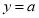з графіком .

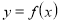Можливі випадки:

1. пряма 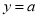не перетинає графік функції 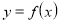. При цьому значення 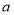рівняння розв’язків не має.
2. пряма 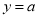перетинає графік функції 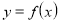. Визначити абсциси точок перетину (для цього достатньо розв’язати рівняння 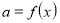відносно ).

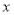5. Записати відповідь

І. Якщо рівняння набуває вигляду

ІІ. Якщо матимемо

У системі координат будуємо графіки функцій для та для

          Далі, знаходимо точки перетину прямої з графіком функції Пряма має з графіком функції лише одну спільну точки, абсциса якої дорівнює

Якщо рівняння розв’язків не має, оскільки пряма не перетинає графік Якщо , пряма перетинає графік функції у двох точках, абсциси яких можна знайти з рівняння

Якщо , то перетином прямої з графіком функції є дві точки з абсцисами де — менший корінь рівняння ; — більший корінь рівняння , тобто

(В. Якщо рівняння розв’язку не має;

; )

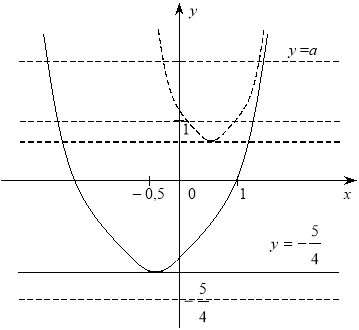
Приклад. При якому значенні рівняння має три розв’язки?

 Запишемо рівняння у вигляді

ОДЗ: ,

Побудуємо схематично графіки функцій та

Якщо , то пряма перетинає криву у трьох точках з абсцисами . (В. )

 

2.Конкурс художників – математиків

МЕТА: виховувати у студентів любов до математики за допомогою малюнків, за допомогою їхньої творчості.

(Малюнки додаються)

Заняття 8

1.Математика різних країн світу. (повідомлення членів гуртка)

2.Розв’язування рівнянь графічним методом.

 

Хід заняття

 

1. Математика різних країн світу

МЕТА: виховувати у студентів любов до математики; ознайомити студентів з розвитком математики в таких країнах: стародавній Єгипет, стародавній Китай, Росія 18-19 століття, давня Греція, стародавня Україна.

(Повідомлення додаються)

 

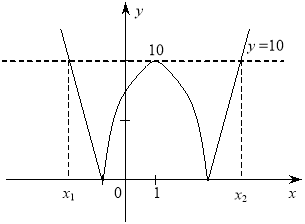
2. Розв’язування рівнянь графічним способом

МЕТА:  поглибити знання студентів про графічний спосіб розв’язання рівнянь; дати студентам алгоритм розв’язання рівнянь графічним способо; навчити розв’язувати рівняння графічним способом, аналізувати, порівнювати, робити висновки щодо розв’язків рівняння.

 

Алгоритм розв’язання рівнянь графічним способом

1. Будуємо в одній координатній площині  окремо графіки лівої і правої частини рівняння.

2. Знайдемо точки перетину графіків.

3. Абсциси точок перетину являються розв’язками даного рівняння.

 

Приклад 1.  х + 2 = х²

f(х) = х+2 Графіком є пряма для побудови якої  потрібно знати 2 точки

Складаємо таблицю.

g(х) = х² графіком функції є парабола.

Складаємо таблицю значень.

Абсциси точок перетину дорівнюють 2 і  -1. Отже ці значення х і є розвязком даного рівняння.

 

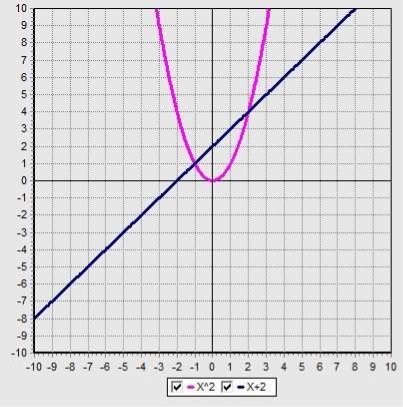
Приклад 2.  х² = ;   

f(х) = х² графіком функції є парабола

g(х) =    Графіком функції є гіпербола, х 0. Складаємо таблицю значень

 

Графіки мають тільки одну спільну точку отже рівняння має тільки один розв’язок

 

 

 

 

 

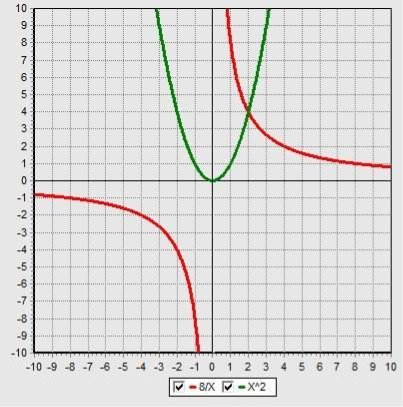
Приклад 3.  |х| = 4.

f(х) = |х| графік функції складається з двох частин: якщо х < 0, то f(х) = -х

якщо, x > 0, то f(х) =  х

якщо х = 0, то f(х) = 0.

 

g(х) = 4 графіком є пряма лінія, яка паралельна осі ОХ і проходить чрез точку (0;4).

 

Абсциси точок перетину дорівнюють 4  і  - Отже ці значення х і є розвязком даного рівняння.

 

 

Заняття 9

Екскурсія в ліс. Підбір матеріалів для виставки «Симетрія в природі»

 

Хід заняття

МЕТА:  прищеплювати любов до природи; показати взаємозв’язок математики з навколишнім середовищем.

 

Гуртківці фотографували та брали з собою «матеріали» природи, в яких проявлялася симетрія.

 

        

    
Заняття 10

1.Виставка «Симетрія в природі»

2.Підведення підсумків роботи математичного гуртка «Лабіринти математики» за навчальний рік.

 

Хід заняття

 

1. Виставка «Симетрія в природі»

МЕТА:  показати де в природі зустрічається симетрія.

 

Гуртківці підготували фото презентацію.