ІНДИВІДУАЛЬНІ ЗАВДАННЯ ДО ВИКОНАННЯ САМОСТІЙНОЇ РОБОТИ З ДИСЦИПЛІНИ «Вища математика» ДЛЯ СТУДЕНТІВ спеціальності 122 «Комп’ютерні науки», Частина 2
Методичні вказівки до виконання самостійної роботи з урахуванням завдань з дисципліни «Вища математика» для студентів спеціальності 122 «Комп'ютерні науки», Перший семестр, частина 2 – Відокремлений структурний підрозділ «Мелітопольський фаховий коледж Таврійського державного агротехнологічного університету імені Дмитра Моторного», 2021 – 25 с.
МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ
Відокремлений структурний підрозділ
«Мелітопольський фаховий коледж Таврійського державного агротехнологічного університету імені Дмитра Моторного»
![]()
Циклова комісія загальноосвітньої підготовки
ІНДИВІДУАЛЬНІ ЗАВДАННЯ
ДО ВИКОНАННЯ САМОСТІЙНОЇ РОБОТИ
З ДИСЦИПЛІНИ «Вища математика»
ДЛЯ СТУДЕНТІВ
спеціальності 122 «Комп’ютерні науки»
Частина 2

Мелітополь, 2021
Методичні вказівки до виконання самостійної роботи з урахуванням завдань з дисципліни «Вища математика» для студентів спеціальності 122 «Комп’ютерні науки», Перший семестр, частина 2 – Відокремлений структурний підрозділ «Мелітопольський фаховий коледж Таврійського державного агротехнологічного університету імені Дмитра Моторного», 2021 – 25 с.
Укладач: Бойко Світлана Борисівна, викладач математичних дисциплін ВСП «МК ТДАТУ», спеціаліст вищої кваліфікаційної
категорії;
ЗМІСТ
|
Вступ Розділ 3. Вступ до математичного аналізу. Розділ 4. Диференціальне числення. Розподіл балів, які отримують студенти Література
|
3
5
14
18
32
40 |
ВСТУП
Методичні вказівки складені відповідно діючій програмі за курсом «Вища математика» для студентів очної форми навчання для спеціальності 122 «Комп’ютерні науки» за I семестр. Методичні вказівки складаються з завдань відповідно програмних питань за наступними темам:
Функція
Абсолютна величина дійсного числа, її властивості. Сталі і змінні величини. Функція, її властивості. Складна функція. Елементарні функції, їх класифікація і графіки. Класифікація функцій. Перетворення графіків. Побудова графіків функцій. Додавання графіків.
Границя змінної величини і неперервність
Границя змінної величини. Единість границі. Нескінченно малі і нескінченно великі величини, їх властивості і зв’язок. Правило граничного переходу. Ознаки існування границі. Поняття про границю функції. Односторонні границі. Перша і друга важлива границі. Порядки нескінченно малих величин. Еквівалентні нескінченно малі величини. Принцип відкидання нескінченно малих величин вищого порядку. Обчислення
границь. Розкриття невизначеностей виду 00 , 0, , 0 ,
00 , 1.
Неперервність функцій в точці і на інтервалі. Умови неперервності функції в точці. Класифікація точок розриву. Властивості функцій неперервних на відрізку.
Диференціальне числення функції однієї змінної
Похідна, її різні змісти. Правила диференціювання суми, добутку, частки. Похідна складеної функції. Диференціювання логарифмічних, степеневих, показникових і степенево-показникових функцій. Логарифмічне диференціювання. Похідні тригонометричних і обернених тригонометричних функцій. Похідні гіперболічних, неявних і параметрично заданих функцій. Похідні вищих порядків.
Застосування диференціального числення для дослідження
функцій і побудови їх графіків
Диференціал функції. Правила та формули обчислення диференціалу. Інваріантність форми диференціала. Застосовування диференціала до наближених обчислень. Теореми Ролля, Лагранжа, Коші. Теореми ЛопіталяБернуллі. Формула Тейлора та Маклорена.
Необхідна і достатня ознаки монотонності функцій. Екстремуми. Теорема Ферма. Перша і друга достатні умови існування екстремуму. Найбільше і найменше значення функції на відрізку. Опуклість і вгнутість кривої. Точки перегину. Достатня ознака опуклості (вгнутості). Асимптоти кривої. Загальна схема дослідження функції.
Мета даних методичних вказівок - закріплення теоретичного матеріалу й придбання практичних умінь для підвищення рівня фундаментальної математичної підготовки студентів із прикладною економічною спрямованістю.
Методичні вказівки містять додатки з довідковим матеріалом.
Розділ3. Вступ до математичного аналізу
Завдання №10. Побудувати графіки функцій
![]() 3 2 x 5
3 2 x 5
10.01. а) y x 6 2
б) y (x 1)3 3
![]() 2 1 x3
2 1 x3
в) y
2
г) y log (![]() x 2)1
x 2)1
д) y 2sin3 x ![]() 3
3
x2
е) y ![]() 13
13
ж) y ![]() x 2 x 1
x 2 x 1
![]() 1 2 2 x 5
1 2 2 x 5
10.03. а) y x
3 3 3
б) y (x 2)3 3
в) y2 x3
г) y log (3 x 1) 2
д) y 3sin4x![]() 6
6
x2
е) y 12 4
2x3
ж) y![]()
x 2
10.05. а) y2x2 8x9
б) y (x 2)3 1
2 ![]() 1 x3
1 x3
в) y
3
г) y log (x 2)2
![]()
д) y 3sin2x![]() 3
3
е) y 2x3 4
ж) y ![]() 2x1 x1
2x1 x1
![]() 1 2 2 x 8
1 2 2 x 8
10.02. а) y x
3 3 3
б) y (x 1)3 2
в) y2 x3
г) y log (4 x 1) 2
д) y 2cos3 x ![]() 4
4
е) y 5x1 3
ж) y ![]() 2x 3 x 1
2x 3 x 1
![]()
![]() 1 2 x 7
1 2 x 7
10.04. а) y x
2 2
б) y (x 2)3 1
![]() 2 1 x3
2 1 x3
в) y
3
г) y log (2 x 1)2
д) y 3cos2 x ![]() 6
6
е) y 4x3 1
2x 1
ж) y ![]()
x 2
10.06. а) y 3x2 18x 25
б) y (x 1)3 1
![]() 2 1 x3
2 1 x3
в) y
4
г) y log (x 3)1
![]()
д) y 2cos4 x ![]() 6
6
е) y 4x1 5
ж) y ![]() 2 x x 1
2 x x 1
![]() 1 2 x3
1 2 x3
10.07. а) y x 2 2
б) y (x 1)3 2
в) y2 (x1)3
г) y log (2 x 2) 3
д) y 4sin2x![]() 3
3
е) y 3x2 1
ж) y 1![]() 2x x 2
2x x 2
10.09. а) y 2x2 8x5
б) y (x2)3 1
![]() 2 1 x3
2 1 x3
в) y
4
г) y log (x4)1
![]()
д) y 4sin3x![]() 4
4
е) y 3x4 2
ж) y 1![]() 2x x1
2x x1
10.11. а) y 2x2 4x![]()
б) y (x 2)3 4
2 ![]() 1 x1)3
1 x1)3
в) y ( 2
г) y log (2 x 3) 4
д) y 3cos2x![]() 3
3
е) y 13 x3 2
ж) y ![]() x1 x3
x1 x3
3 ![]() 2 x 3
2 x 3
10.08. а) y x 6 2
б) y (x 3)3 2
![]() 2 1 x3
2 1 x3
в) y
2
г) y log (2 x 3)5
д) y 2cos3 x ![]() 3
3
x2
е) y ![]() 15 3
15 3
ж) y ![]() 1 x x 2
1 x x 2
10.10. а) y 3x2 12x 11
б) y (x 1)3 2
в) y2 (x 1)3
г) y log (x 4)2
![]()
д) y 4cos3 x ![]() 4
4
x1
е) y ![]() 13 3
13 3
ж) y 1![]() 2x x 1
2x x 1
10.12. а) y 2x2 4x 6
б) y (x 2)3 4
в) y2 ![]() (x 1)3
(x 1)3
г) y log (3 x 2) 4
д) y 3sin2 x ![]() 3
3
x3
е) y ![]() 14 2
14 2
ж) y ![]() x 1 x 3
x 1 x 3
![]() 1 2 x1
1 2 x1
10.13. а) y x 2 3
б) y (x1)3 3
2 ![]() 1 x 2)3
1 x 2)3
в) y ( 3
г) y log (![]() x 3) 2
x 3) 2
3 ![]() 2 x5
2 x5
10.14. а) y x 6 2
б) y (x 2)3 4
2 ![]() 1 x3
1 x3
в) y
4
г) y log (x 4) 2
![]()
д) y 4cos2x![]() 3
3
е) y 4x2 3
ж) y 1![]() 3x x1
3x x1
![]() 1 2 2 x 8
1 2 2 x 8
10.15. а) y x
3 3 3
б) y (x 3)3 2
2 ![]() 1 x3
1 x3
в) y
4
г) y log (2 x4)1
![]() 13x д) y 2sin 3
13x д) y 2sin 3
е) y 13 x2 1
ж) y ![]() 3x2 x2
3x2 x2
![]() 1 2 2 x 5
1 2 2 x 5
10.17. а) y x
3 3 3
б) y (x3)3 1
в) y2 2x3
г) y log (2 x 3) 4
д) y 2cos3x![]() 4
4
е) y 3x2 1
ж) y 1![]() x x1
x x1
д) y 2cos3x![]() 4
4
е) y 3x4 2
ж) y ![]() 3x1 x1
3x1 x1
![]() 3 2 x 3
3 2 x 3
10.16. а) y x 6 2
б) y (x 3)3 2
в) y2 ![]() (x 1)3
(x 1)3
г) y log (x 1) 2
![]()
д) y 2sin3 x ![]() 3
3
е) y 2x3 2
ж) y ![]() 3x 7 x 3
3x 7 x 3
1.18. а) y 2x2 8x 9
б) y (x 3)3 2
в) y2 2(x 2)3
г) y log (![]() x 2)1
x 2)1
д) y 3sin4 x ![]() 6
6
е) y ![]() 13x2 1
13x2 1
ж) y ![]() 23x x 1
23x x 1
10.19. а) y 3x2 18x 25
б) y (x1)3 4
в) y2 2(x1)3
г) y log (3 x 3) 2
д) y 3sin2x![]() 3
3
x2
е) y 12 3
ж) y ![]() x4 x2
x4 x2
10.21. а) y 2x2 8x5
б) y (x2)3 4
в) y2 (x 3)3
1 ![]() 2 x 3
2 x 3
10.20. а) y x 2 2
б) y (x 1)3 3
2 ![]() 1 x 2)3
1 x 2)3
в) y ( 3
г) y log (3 x 2) 4
д) y 2cos4 x ![]() 6
6
е) y 2x3 2
3x 1
ж) y ![]()
x 1 10.22. а) y 3x2 12x 11
б) y (x 2)3 3
|
г) y log ( |
в) y2 (x 3)3
д) y 4sin2x![]() 3
3
е) y 3x4 1
3x7
ж) y![]()
x3
1 ![]()
![]() 2 x 7
2 x 7
10.23. а) y x
2 2
б) y (x 1)3 4
![]() 2 1 x3)3
2 1 x3)3
в) y ( 2
г) y log (![]() x4) 2
x4) 2
д) y 4sin3x![]() 4
4
е) y 2x4 3
ж) y ![]() x3 x1
x3 x1
д) y 2cos3 x ![]() 3
3
е) y 3x3 2
2x 4
ж) y ![]()
x 3
10.24. а) y 3x2 12x 6
б) y (x 2)3 3
в) y2 ![]() (x 3)3
(x 3)3
г) y log (3 x 2)4
д) y 4cos3 x ![]() 4
4
x2
е) y ![]() 12 1
12 1
ж) y ![]() 2x 4 x 3
2x 4 x 3
1 ![]()
![]() 2 x13
2 x13
10.25. а) y x 3
2 2
б) y (x 2)3 3
в) y2 (x 2)3
г) y log (2 x 3) 2
д) y 3cos2x![]() 3
3
x1
![]() е) y 3
е) y 3
ж) y ![]() 32x x1
32x x1
10.26. а) y 2x2 12x 19
б) y (x 2)3 2
в) y2 (x 2)3
г) y log (x 3) 2
![]()
д) y 3sin2 x ![]() 3
3
е) y 2x2 3
ж) y ![]() 32x. x 3
32x. x 3
Завдання №11. Побудувати графіки функцій за допомогою графічного додавання та знайти величину найбільшої амплітуди
11.01. y![]() sin xcosx 11.02. y sin2xcosx
sin xcosx 11.02. y sin2xcosx
11.03. y 3sin2x![]() cosx 11.04. y 2sin xcos2x
cosx 11.04. y 2sin xcos2x
![]() x
x
11.05. y2sin xcos ![]() 11.06. y sin x 2cos2x
11.06. y sin x 2cos2x
2
|
11.07. ysin2x3cosx |
11.08. y3sin xcos2x |
11.09. y![]() sin2xcosx 11.10. y 2sin x
sin2xcosx 11.10. y 2sin x![]() cosx
cosx
![]() x 11.11. y sin xcos2x 11.12. y sin
x 11.11. y sin xcos2x 11.12. y sin ![]() cosx
cosx
2
11.13. y3sin2x![]() cosx 11.14. y2sin xcos2x
cosx 11.14. y2sin xcos2x
11.15. ysin2x3cosx 11.16. y 3sin x![]() cosx
cosx
11.17. y![]() sin xcos2x 11.18. y sin2xcosx
sin xcos2x 11.18. y sin2xcosx
11.19. y 3sin2x![]() cos2x 11.20. y 2cosxsin2x
cos2x 11.20. y 2cosxsin2x
![]() x
x
11.21. y2cosxsin ![]() 11.22. y cosx 2sin2x 2
11.22. y cosx 2sin2x 2
11.23. ysin2x3cos2x
11.24. y3sin xcos2x
1 ![]() x
x
11.25. y ![]() sin2xcos
sin2xcos ![]() 11.26. y sin x cos2x.
11.26. y sin x cos2x.
2 2
Завдання №12. Методом графічного додавання скласти два струми i1 A1sin(wt 1)та i2 A2 sin(wt 2)враховуючи, що
![]()
![]() i1 i2 A12 2A1A2 cos(2 1) A22 sinwt arccos A12 A12cosA1A21cos( A22cos12) A22 ,
i1 i2 A12 2A1A2 cos(2 1) A22 sinwt arccos A12 A12cosA1A21cos( A22cos12) A22 ,
де A1, A2 – амплітуди; w– частота; 1,2– початкові фази
|
12.01 |
i1 2sin2t |
i2 2sin2t 6 |
|
12.02 |
i1 2sin2t |
i2 2sin2t 4 |
|
12.03 |
i1 2sin2t |
i2 2sin2t 3 |
|
12.04 |
i1 sin2t |
i2 2sin2t 6 |
|
12.05 |
i1 sin2t |
i2 2sin2t 4 |
|
12.06 |
i1 sin2t |
i2 2sin2t 3 |
|
12.07 |
i1 2sin2t |
i2 sin2t 6 |
|
12.08 |
i1 2sin2t |
i2 sin2t 4 |
|
12.09 |
i1 2sin2t |
i2 sin2t 3 |
|
12.10 |
i1 sin2t |
i2 2sin2t 6 |
|
12.11 |
i1 sin2t |
i2 2sin2t 4 |
|
12.12 |
i1 sin2t |
i2 2sin2t 3 |
|
12.13 |
1 i1 |
i2 2sin3t 6 |
|
12.14 |
1 i1 |
i2 2sin3t 4 |
|
12.15 |
1 i1 |
i2 2sin3t 3 |
|
12.16 |
i1 2sin3t |
1 i2 2 4 |
|
12.17 |
i1 2sin3t |
1 i2 2 3 |
|
12.18 |
i1 2sin3t |
1 i2 2 6 |
|
12.19 |
1 i1 |
i2 2sin3t 6 |
|
12.20 |
1 i1 |
i2 2sin3t 4 |
|
12.21 |
1 i1 |
i2 2sin3t 3 |
|
12.22 |
i1 2sin3t |
1 i2 2 6 |
|
12.23 |
i1 2sin3t |
1 i2 2 4 |
|
12.24 |
i1 2sin3t |
1 i2 2 3 |
|
12.25 |
i1 3sin2t |
i2 2sin2t 6 |
|
12.26 |
1 i1 |
i2 sin3t 3 |
Завдання №13. Знайти границі, розкриваючи невизначеності виду 00 , та використовуючи першу і другу визначні границі
13.01. а) limx3![]() 3x28 xx36x[1]
3x28 xx36x[1]
2x2 x 3 б) limx x3 3x1
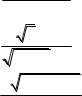 в) limx4 2xx 12 3
в) limx4 2xx 12 3
г) limx0 x sin 312cos4x x
д) limx ![]() 22xx153 2x
22xx153 2x
2x2 17x35
13.03. а) limx5 ![]() x2 х 20
x2 х 20
3x2 4x1
б) limx x3 3x4
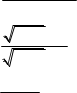 в) limx0 9x 4х 32
в) limx0 9x 4х 32
sin6x
г) lim
x0 tg2x
д) limx ![]() 22xx134x
22xx134x
2 2x 1
3x
13.05. а) limx1 ![]() x3 1
x3 1
23x x 2
б) limx 2x2 x 1
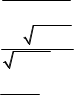 5 x2 9
5 x2 9
в) lim
x4 2x 1 3
г) lim 3x x0 sin2x
2x2 7x 4
13.02. а) limx4 ![]() 43x x 2 x3 8x 1 б) limx 3x2 x 4
43x x 2 x3 8x 1 б) limx 3x2 x 4
2x 3 3
в) lim
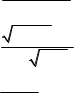 x3 2 x 1 sin5x
x3 2 x 1 sin5x
г) lim
x0 sin3x
д) limx ![]() 33xx12 2x4
33xx12 2x4
9x 2x2 10
13.04. а) limx2 ![]() x2 x 2
x2 x 2
3x2 4x 1
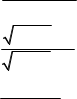 б) limx 2x2 x 3 x2 9 3
б) limx 2x2 x 3 x2 9 3
в) lim
x0 4 x2 2 tg 32 x
г) lim
x0 1cos4x
д) lim 1x ![]() 3x211 3 x
3x211 3 x
![]() 13.06. а) lim x2
13.06. а) lim x2
2x3 x 1 б) limx x2 2x 5
![]() в) limx2 3xx2242
в) limx2 3xx2242
г) limsin3xctg2x
x0
д) lim 1 ![]() 2x314x1 x
2x314x1 x
3x2 5x 2
13.07. а) limx1 ![]() 2x2 x 1
2x2 x 1
2x2 3x1
б) limx x2 x 5
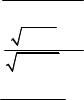 в) limx3 3x 24x 13
в) limx3 3x 24x 13
г) limx0 1sin 3cos42 xx
д) lim 1 ![]() x2 4 2x 1 x
x2 4 2x 1 x
2x2 x 3
13.09. а) limx1 ![]() x2 3x4
x2 3x4
2x2 3x1
б) limx x3 2x3
![]() в) limx2 xx 2 64 2
в) limx2 xx 2 64 2
sin2x
г) lim![]()
x0 tg3x
4x
д) limx ![]() 33xx52
33xx52
2x2 7х3
13.11. а) limx3 ![]() x2 2x3
x2 2x3
3x2 4x 2
б) limx x2 x 5
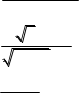 в) limx4 1x2x23
в) limx4 1x2x23
sin6x
г) lim
x0 2tg3x
д) lim 1 ![]() x233 1x x
x233 1x x
![]() 13.08. а) lim x2
13.08. а) lim x2
2x3 3x1 б) limx 3x3 x2 4
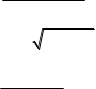 в) limx x2 2x
в) limx x2 2x
x arcsin6x
г) lim
x0 2x
д) limx ![]() 22xx133x4
22xx133x4
7x x 2 12
13.10. а) limx3 ![]() 2x2 11x 15
2x2 11x 15
3x2 2x 1
б) limx x2 3x 4
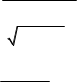 в) lim 4x2 x 2x x
в) lim 4x2 x 2x x
arctg3x
г) lim
x0 2x
д) lim 1 ![]() 3x21x2 x
3x21x2 x
![]() 13.12. а) lim x3
13.12. а) lim x3
x3 2x 1
 б) limx 5x2 4x 2 x2 5 3
б) limx 5x2 4x 2 x2 5 3
в) limx2 х2 4 sin 32 x
г) limx0 ![]() x2
x2
д) lim 1 ![]() 2x534x1 x
2x534x1 x
13.13. а) limx2 ![]() 32xx22107хx68 13.14. а) limx2
32xx22107хx68 13.14. а) limx2 ![]() 32xx227xх62
32xx227xх62
3x2 4x1 2x2 3x 1
б) limx 2x2 x 4 б) limx 3x3 x 4
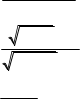
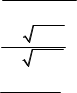 в) limx0 х22 161 14 в) limx4 13 55xx
в) limx0 х22 161 14 в) limx4 13 55xx
х
г) lim 2 x г) limx0 cos4x2 x x2 1
x 0 tg 3
3 2x1 д) lim ![]() 33xx52 6x5
33xx52 6x5
д) lim 1 ![]() 4x1 x x
4x1 x x
13.15. а) limx1 ![]() 2x2x3 x1 3 13.16. а) limx3
2x2x3 x1 3 13.16. а) limx3 ![]() 26x27х7x3x32
26x27х7x3x32
23x x 3 2x2 3x 2
![]() б) limx 3x2 x 3 б) limx x2 x 4
б) limx 3x2 x 3 б) limx x2 x 4
 в) limx0 1 x x 1x в) limx1 51х2x 2
в) limx0 1 x x 1x в) limx1 51х2x 2
г) lim x sin4x
 x0 1cos3x г) limx0 2(1cos4 )x
x0 1cos3x г) limx0 2(1cos4 )x
3 1x
 д) limx 22xx11 д) limx 33xx 42 4x3
д) limx 22xx11 д) limx 33xx 42 4x3
3x2 5x2 2x2 7x5
13.17. а) limx2 ![]() 67x 2x2 13.18. а) limx1
67x 2x2 13.18. а) limx1 ![]() 2x2 x 1
2x2 x 1
2x3 2x3 3x2 4x1
б) lim x2 x 1 б) limx 2x3 x 2 x
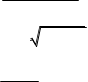
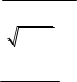 в) limxx x2 6x в) limx x2 1 x sin6x arcsin4x
в) limxx x2 6x в) limx x2 1 x sin6x arcsin4x
г) lim г) lim
x0 sin3x x0 2x
д) lim 1x ![]() x 233 1x д) limx
x 233 1x д) limx ![]() 22xx13x1
22xx13x1
3x2 2x 8 x2 3x 4
13.19. а) limx2 ![]() 23x 2x2 13.20. а) limx4
23x 2x2 13.20. а) limx4 ![]() x2 9x 20
x2 9x 20
12x 3x2 2x3 3x 4 б) limx 2x2 x 3 б) limx ![]() 4x3 x2 1
4x3 x2 1
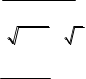
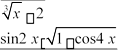 в) limx x 2 x в) limx8 x 8 arctg6x
в) limx x 2 x в) limx8 x 8 arctg6x
г) lim
x0 2x г) lim 2
3 2x x 0 6x
![]()
д) limx 44xx13 д) lim x ![]() xx332x5
xx332x5
x2 3x 2 3x2
13.21. а) limx1 ![]() 2 4x1 13.22. а) limx2
2 4x1 13.22. а) limx2 ![]() x2 xx106
x2 xx106
3x
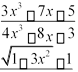 8x4 x 4
8x4 x 4
б) limx б) limx 32x2
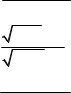 в) limx0 x2 x3 в) limx3 xx 12 21
в) limx0 x2 x3 в) limx3 xx 12 21
г)lim ![]() cos xcosa г) lim ctgx ctga x a x a x a x a
cos xcosa г) lim ctgx ctga x a x a x a x a
x2 x 3
д) lim![]() x2 12 2 д) limx
x2 12 2 д) limx ![]() xx852x3
xx852x3
x
![]() 2x2 x 3 13.23. а) limx2 13.24. а) limx1
2x2 x 3 13.23. а) limx2 13.24. а) limx1 ![]() 3x2 2x 1
3x2 2x 1
![]()
![]() б) lim б) lim
б) lim б) lim
xx
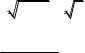
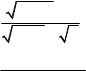 в) limx x 2 x в) lim 2х 1 3 arcsin2x x4 х 2 2
в) limx x 2 x в) lim 2х 1 3 arcsin2x x4 х 2 2
г) lim cos x cos3 x x 0 3x г) limx0 x2
![]()
![]() д) lim x x 2 3 1x д) limx 22xx112x1 x
д) lim x x 2 3 1x д) limx 22xx112x1 x
x2 4x3
13.25. а) limx3 ![]() 2x2 9x9
2x2 9x9
б) limx x34 x12x5x41
1 x 1x2
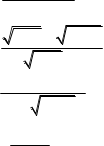 в) limx0 1 х 1
в) limx0 1 х 1
г) lim cos xcos3x
x0 1 1x2
x2
д) lim 33xx 42 . x
Завдання №14. Обчислити границю функції за допомогою принципу заміни еквівалентних нескінченно малих величин
|
etg3x 14.01. limx0 |
esin2x 14.02. limx0 |
![]()
![]() 14.03. limx0 11cos4x22x114.04. limx0 1arctg2sin xx1
14.03. limx0 11cos4x22x114.04. limx0 1arctg2sin xx1
sin3x ln(1 tg2 )x
![]()
![]() 14.05. limx0 1 tg2x114.06. limx0 1 5 x 1
14.05. limx0 1 tg2x114.06. limx0 1 5 x 1
![]() 14.07. limx0 ln(1 2 )xx arctg
14.07. limx0 ln(1 2 )xx arctg
1x2
![]() 41 4x2 1
41 4x2 1
14.08. limx0 sin 32 x
tg(e2x
![]() 14.09. limx0 ln(1 3 )x1)
14.09. limx0 ln(1 3 )x1)
ln x
![]() 14.10. limx1 sin(ex1 1)
14.10. limx1 sin(ex1 1)
ln(1 4 )x 31 3 x 1
![]() 14.11. limx0
14.11. limx0 ![]() arcsin2x 14.12. limx0 1 tg2x1
arcsin2x 14.12. limx0 1 tg2x1
|
sin2 x 14.13. limx0 |
14.14. limx0 |
|
tg(e3x 14.15. limx0 |
14.16. limx0 ln(1 4x2) |
|
e2x 14.17. limx0 |
ex1 14.18. limx1 |
![]() ex2 1
ex2 1
![]() 14.19. limx0 1 4х2 114.20. limx0
14.19. limx0 1 4х2 114.20. limx0
|
lim |
e3tgx 1 |
tg5x lim |
![]() 14.21. x0 13х 1 14.22. x0 earcsin2x 1
14.21. x0 13х 1 14.22. x0 earcsin2x 1
|
14.23. x0 earctg2x 1 |
14.24. x0 |
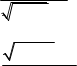 4 1 2x 1 sin2x limlim
4 1 2x 1 sin2x limlim
![]()
![]() 1 x2 1
1 x2 1
14.25. limx0 sin 22 x 14.26. limx2.
Завдання №15. Дослідити функції на неперервність. Знайти точки розриву і границі функцій ліворуч і праворуч від точки розриву. Зробити схематичний графік
|
2х5, якщо х1 15.01 а) у 2 4 , якщо х1 х х |
1
б) у 2х1 |
|
х2 2, якщо х 2 15.02 а) у 7х, якщо х 2 |
1
б) у3х2 |
|
2х1, якщо х2 15.03 а) у 2 1, якщо х2 х |
1
б) у 21х |
|
2хx2, якщо х 3 15.04 а) у 2x, якщо х 3 |
1
б) у31х |
|
4хx2, якщо х 3 15.05 а) у 2x5, якщо х 3 |
1 б) у5 х |
|
х4, якщо х2 15.06 а) у 2 2, якщо х2 х |
1
б) у2 х |
|
х2 3, якщо х1 15.07 а) у х2, якщо х1 |
1
б) у2х2 |
|
x2 3, якщо х 2 15.08 а) у x1, якщо х 2 |
1 б) у3 х |
|
х5, якщо х1 15.09 а) у 2 1, якщо х1 х |
1
б) у4х2 |
|
x2 1, якщо х 2 15.10 а) у 2x3, якщо х 2 |
1 б) у4 х |
|
x3, якщо х 0 15.11 а) у x2, якщо х 0 |
1
б) у32х |
|
x3 1, якщо х1 15.12 а) у x1, якщо х1 |
1 б) у2 х |
|
x3 1, якщо х1 15.13 а) у x 2, якщо х1 |
1
б) у41х |
|
x2, якщо х 2 15.14 а) у x 3, якщо х 2 |
1
б) у3х2 |
|
x3 1, якщо х1 15.15 а) у x2, якщо х1 |
1
б) у23х |
|
x 2, якщо х 2 15.16 а) у 2 1, якщо х 2 x |
1
б) у2х3 |
|
x2 4, якщо х1 15.17 а) у |
1
б) у3х1 |
42х, якщо х1
|
2х, якщо х 3 15.18 а) у 2, якщо х 3 0,1x |
1
б) у3х3 |
|
x2, якщо х 3 15.19 а) у 2x1, якщо х 3 |
1
б) у2 х4 |
|
x2 1, якщо х1 15.20 а) у x1, якщо х1 |
1
б) у2 4х |
|
x2, якщо х1 15.21 а) у 2x, якщо х1 |
1
б) у3х4 |
|
2х1, якщо х 0 15.22 а) у 3 1, якщо х 0 x |
1
б) у4х3 |
|
x1, якщо х1 15.23 а) у 2, якщо х1 x |
1
б) у4 х1 |
|
х1, якщо х1 15.24 а) у 3, якщо х1 x |
1
б) у32х |
|
4х2, якщо х 3 15.25 а) у х2, якщо х 3 |
1
б) у4х3 |
|
x2 1, якщо х 2 15.26 а) у 4x, якщо х 2
|
1
б) у2х3 . |
Розділ4. Диференціальне числення
Завдання №15. Знайти похідні функцій
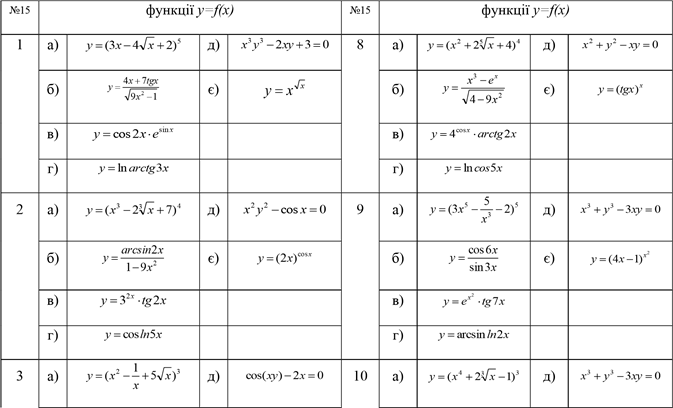
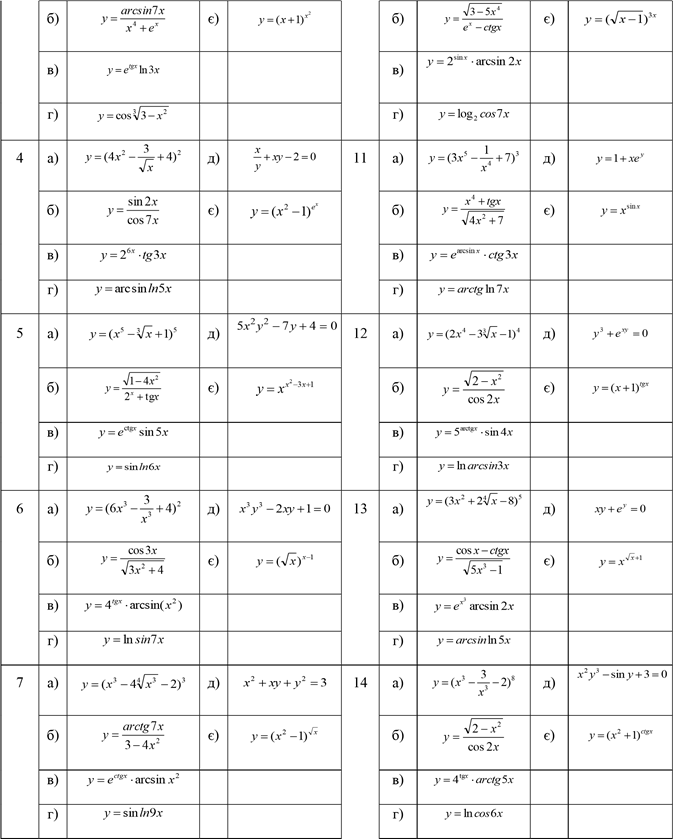
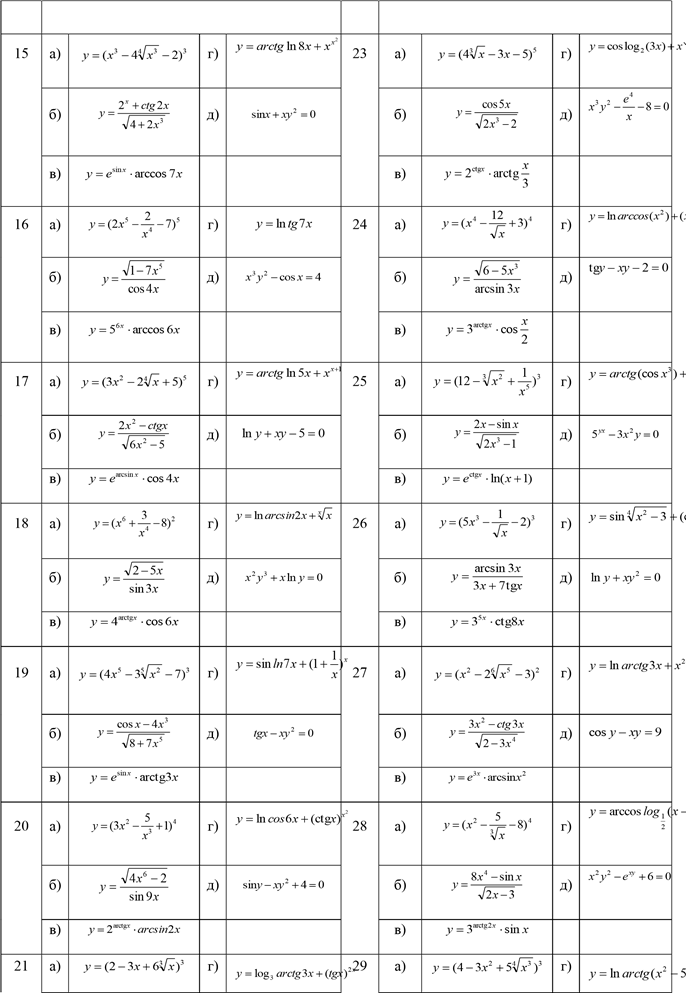 |
Завдання 16. Обчислити границі за допомогою правила Лопіталя - Бернуллі
x4
16.1. а) limx1 ![]() x11 б) limx0 xln x
x11 б) limx0 xln x
16.2. а) limx2 ![]() xx5 322 б) limx0 xctg3x
xx5 322 б) limx0 xctg3x
16.3. а) limx0 ![]() esinx x1 б) limx0(1cos x)ctgx
esinx x1 б) limx0(1cos x)ctgx
ln x tg x
 |
16.4. а) limx1
16.5. а) limx01![]() ecosx 12x б) limx1x
ecosx 12x б) limx1x![]() ln1x
ln1x
16.6. а) limx0 11![]() coscos43xx б) limx0(ctgx)sinx
coscos43xx б) limx0(ctgx)sinx
16.7. а) limx011![]() coscos42xx б) limx2 tgxctg3x
coscos42xx б) limx2 tgxctg3x
![]()
e ex x x
16.8. а) limx0 ![]() sin x б) limx( x)tg
sin x б) limx( x)tg![]() 2
2
16.9. а) limx1 ![]() xlnx1 б) limx2( 2x)cosx
xlnx1 б) limx2( 2x)cosx
![]()
16.10. а) limx0 ![]() sin2x б) limx1(1 x)tg
sin2x б) limx1(1 x)tg![]() 2x e2x 1
2x e2x 1
e2x
16.11. а) limx0 1![]() cos1x б) limx0 xctgx
cos1x б) limx0 xctgx
1
![]()
16.12. а) limx0 ![]() xxsin2 x б) limx0(cos2x)x2
xxsin2 x б) limx0(cos2x)x2
ln x ![]() 1
1
16.13. а) limx![]() x 2 б) limx1 x1x
x 2 б) limx1 x1x
16.14. а) 3 x б) lim(tgx)tg2x
![]()
limx ln2x x![]() 4
4
x2
16.15. а) limx![]() e2x б) limx0 xsin x
e2x б) limx0 xsin x
ln x  1
1
16.16. а) limx ![]() e3x б) limx0 x1ln x
e3x б) limx0 x1ln x
ln x ![]() 1
1
16.17. а) limx0 ![]() ctg x б) limx(1ex)x
ctg x б) limx(1ex)x
ex
16.18. а) limx ![]() x2 б) limx0(1e2x)ctgx
x2 б) limx0(1e2x)ctgx
x
16.19. а) limx ![]() ln (1x) б) limx0 ctg4x(e3x 1)
ln (1x) б) limx0 ctg4x(e3x 1)
tg x
![]() 16.20. а) limб) limx0 x3 ln x x tg 3x
16.20. а) limб) limx0 x3 ln x x tg 3x
2
3x3
16.21. а) limx ![]() x3 2xx2 1x б) limx1 (x 1)2 ln(x 1)
x3 2xx2 1x б) limx1 (x 1)2 ln(x 1)
x3
16.22. а) limx![]() e3x б) limx0 xlnsin x
e3x б) limx0 xlnsin x
x lim(
16.23. а) lim ![]() б) x 2x)tgx x ln x
б) x 2x)tgx x ln x ![]() 2
2
ln x limsin(2x
16.24. а) limx0 ![]() lnsin x б) x
lnsin x б) x![]() 12 1)tgx
12 1)tgx
ln2 x sin x 16.25. а) limx ![]() x3 б) limx0
x3 б) limx0 ![]() 1x
1x
![]()
16.26. а) limx1 ![]() ctgln(x1)x б) limx0 x .
ctgln(x1)x б) limx0 x .
Завдання 17. Дослідити функції та побудувати їх графіки
x3
![]() 17.01. y
17.01. y ![]() 3(3 2) 17.14. y xx212
3(3 2) 17.14. y xx212
x
4x
17.02. y ![]() x2 4 17.15. y 4 xex3
x2 4 17.15. y 4 xex3
17.03. y x2 ex 17.16. y ![]() x5x4 8
x5x4 8
x2
![]() 17.04. y
17.04. y ![]() 4 x2 17.17. y 3 6x2 x3
4 x2 17.17. y 3 6x2 x3
![]() x
x
17.05. y 4 ![]() x2 21x2 4 17.18. y 2xx3 12
x2 21x2 4 17.18. y 2xx3 12
x3
17.06. y x2e3x 17.19. y ![]() x2 4
x2 4
3x x3
17.07. y ![]() 3x 17.20. y
3x 17.20. y ![]() 2x 22
2x 22
x 1
2x3 3x4
17.08. y ![]() x2 1 17.21. y
x2 1 17.21. y ![]() x31
x31
x3 4 x3
17.09. y ![]() 2 17.22. y
2 17.22. y ![]() x2 4
x2 4
x
4x2 x2
17.10. y ![]() x2 3 17.23. y
x2 3 17.23. y ![]() xx2 6
xx2 6
8x
17.11. y 2x 3ex 17.24. y ![]() x2 4
x2 4
x3 x2
17.12. y ![]() 2 17.25. y
2 17.25. y ![]() x12
x12
3 x
17.13. y ![]() 17.26. y
17.26. y ![]() x212 . x2 x x 1
x212 . x2 x x 1
Завдання 18. Знайти найбільше та найменше значення величин
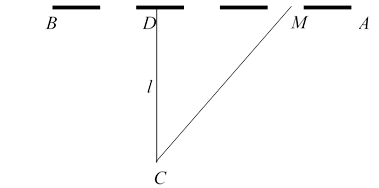
По прямій AB прокладено залізницю. В стороні від неї на відстані l розташовано пункт C (CD l ). Потрібно перевезти вантаж з пункту C до пункту A, який розташовано на відстані 1000 км. від D. У яку точку M залізниці найвигідніше привезти вантаж з пункту C , щоб далі його транспортувати залізницею, якщо вартість перевезень на 1 км.
автотранспорту у mразів дорожче, ніж залізницею m1? Знайти вартість перевозу.
|
№ варіанту |
Параметри |
№ варіанту |
Параметри |
||
|
l |
m |
l |
m |
||
|
1 |
10 |
1,1 |
14 |
80 |
1,7 |
|
2 |
15 |
1,2 |
15 |
85 |
1,6 |
|
3 |
20 |
1,3 |
16 |
90 |
1,8 |
|
4 |
25 |
1,9 |
17 |
95 |
1,5 |
|
5 |
30 |
1,8 |
18 |
100 |
1,9 |
|
.6 |
35 |
1,7 |
19 |
105 |
1,4 |
|
7 |
40 |
1,6 |
20 |
115 |
2,0 |
|
8 |
45 |
1,5 |
21 |
120 |
1,3 |
|
9 |
50 |
1,4 |
22 |
125 |
2,1 |
|
10 |
55 |
2,0 |
23 |
130 |
1,2 |
|
11 |
60 |
2,1 |
24 |
135 |
2,2 |
|
12 |
65 |
2,2 |
25 |
140 |
1,1 |
|
13 |
70 |
2,3 |
26 |
145 |
2,3 |
ЛІТЕРАТУРА
1. Пискунов Н. С. Дифференциальное и интегральное исчисления. Для ВТУЗов, т. 1: Учебное пособие для ВТУЗов. – 12 – е изд. – М.: Наука, 1978 – 456с.
2. Валєєв К. Г., Джалладова І. А. Вища математика: Навч. посібник: У 2 – х ч. – К.: КНЕУ, 2001 – Ч.1. – 546с. 3. Высшая математика для экономистов: Учебник для вузов / Н. Ш. Кремер, Б. А. Путко, И. М. Тришин, М. Н. Фридман; под ред. проф. Н. Ш. Кремера. – 2 – е изд., перераб. и доп. – М.: ЮНИТИ, 2002 – 471с.
4. Дубовик В. П., Юрик І. І. Вища математика: Навч. посібник. – К.: А.С.К., 2001 – 648с.


про публікацію авторської розробки
Додати розробку
