Інтеграл і його застосування

 

 

 

 

 

 

Урок на тему:

 

 

„Інтеграл і його застосування”

 

 

 

 

 

 

                                              Підготувала

                                                             Вчитель математики

      Прилуцького ліцею № 6

                                                   Кривошей І.О.

 

 

 

 

 

м.Прилуки

 

2013р.

 

Тема:   Інтеграл і його застосування.

Мета:  систематизувати знання учнів з теми „Інтеграл і його                                                                                                                                                               

            застосування”, формувати вміння та навички використання

            отриманих знань під час розв’язування вправ на знаходжен-

            ня невизначених і визначених інтегралів, обчислення площ                   

            криволінійних фігур, об’ємів тіл обертання, фізичних

            величин, розвивати логічне мислення, сприяти свідомому  

            застосуванню вивченого матеріалу під час розв’язування

            вправ, розвивати вміння орієнтуватись в нестандартних

            ситуаціях, виховувати інтерес до процесу навчання, вміння

            звертатись до власного досвіду, культуру математичної  мо-

            ви.

Тип уроку: урок систематизації знань, умінь і навичок.

Обладнання: мультимедійна дошка, проектор, презентація, картин-

                       ки, тести.

Хід уроку.

                                  Світ, що нас оточує –

                                  це світ інтегрального і

диференціального числення,

Тож давайте його пізнавати.

                               Х. Гюгенс.

І. Організаційний момент

Використовуючи інтерактивну технологію „Мікрофон”, учні називають вивчені терміни та поняття з теми.

ІІ. Актуалізація опорних знань

Фротальне опитування.

На екран проектується слайд із таблицею. Заповнити таблицю.

 

	?	tg x	?	sin x
		?		cos x

 

Запитання.

1. Які операції виконували?

2. Що називається первісною функції?

3. Хто ввів термін „первісна”?

4. Що називається невизначеним інтегралом функції?

5.Хто ввів символ        і  поняття невизначеного інтеграла?

6.Знайти невизначені інтеграли (слайд з умовами на екрані).

7.Що є криволінійною трапецією?(Зображення на слайді).

 

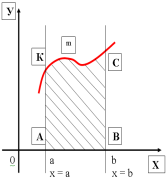
8.Що називається визначеним інтегралом?

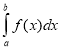9.Формула Ньютона-Лейбніца.

10.Хто ввів позначення               ?

 

11. Які з фігур є криволінійними трапеціями?(слайд із фігурами).

 

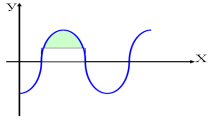
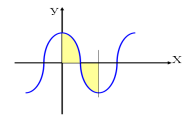
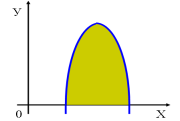
ІІІ.Повторення, узагальнення та систематизація вмінь і навичок

Учні об”єднуються у три групи. Перша і друга виконують завдання самостійно, третя працює з учителем.

Завдання для 1-ї групи (Індивідуальні тестові завдання з використанням програмованого контролю.)

  

1- й варіант

1. Загальний вигляд первісної для функції   ƒ(x) =

А. .  Б. .   В. .   Г. .

2. Знайти  

А. ctg x + C.   Б. – sin x + C.   В. tg x + C.   Г. cos x + C.

3. Обчислити інтеграл    .

А. 8.       Б. 4.       В. 3.       Г. 2.

4. Обчислити інтеграл   .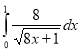

А. 5.       Б. 8.       В. 2.       Г. 4.

5. Записати у вигляді визначеного інтеграла площу фігури, обмеженої лініями ,

А. .   Б. .   В. .   Г. Інша відповідь.

2-й варіант

1. Загальний вигляд первісної для функції   ƒ(x) = .

А.  .   Б.  .   В. .   Г. .

2. Знайти   .

А. tg x + C   Б. cos x + C   В. –ctg x + C   Г. –sin x + C.

3. Обчислити інтеграл   .

А. 9       Б.3.       В.27.       Г.6.

4. Обчислити інтеграл   .

А. 7       Б. 8.      В. 6.         Г. 2.

5. Записати  у вигляді визначеного інтегралу площу фігури, обмеженої лініями .

А. .   Б. .   В. .   Г. Інша відповідь.

Програмований контроль.

Учитель заздалегідь готує тестові бланки відповідей однакового формату для учнів і один для себе. На своєму бланку він робить отвір у клітинці, що відповідає правильній відповіді. Шляхом накладання бланків один на один можна перевірити правильність відповідей.

Приклад бланка відповідей.

 

Прізвище, ім’я
	А	Б	В	Г
1		+
2			+
3	+
4				+
5	+

 

Завдання для 2-ї групи

(Робота в парах)

 

 

 

 

 

 

 

 

1. Записати за допомогою інтеграла площу фігури, зображеної на малюнку, та обчислити.

2. Знайти площу фігури, обмеженої параболою              та прямими

 

  y = 0, x = -2, x = -1. (2   кв. од.).

3.Знайти площу фігури обмеженої графіком функції                 та

 

прямими y = 0, х = 1 і х = 9(17    кв. од.).

4. Знайти площу фігури, обмеженої графіком функції                 та

 

прямими у = 0, х = 1.(     кв. од.).

(Учні записують відповіді на окремих аркушах з клейким краєм і наклеюють їх як листочки на зображення дерева).

Працювати з 1-ю та 2-ю групами допомагають учителю 2 помічни-

ка.

Завдання для 3-ї групи

Учні працюють біля дошки (2 учня 3-ї групи, останні на місцях).

1. Знайти площу фігури, обмеженої параболою                      та прямою у = 5-х (4,5 кв. од.).

2. Знайти площу фігури, обмеженої графіком функції   

та віссю абсцис. (10 кв. од.).

IV. Колективне розв’язування нестандартного завдання :

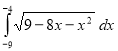
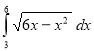
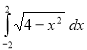
Використовуючи геометричної зміст інтегралу, обчислити:

Завдання на слайді (зображення геометричного змісту).

      

 

 

  

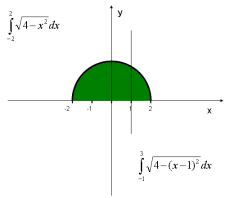
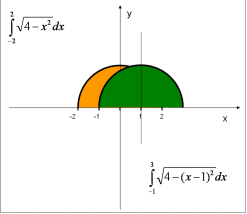
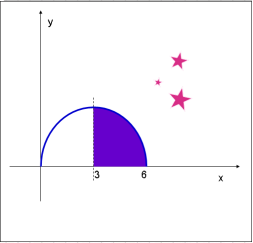
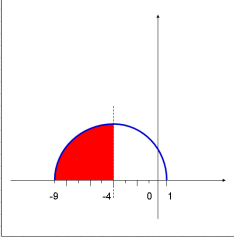
V. Колективне розв’язування вправ на застосування інтеграла для знаходження об’єму тіла обертання, для знаходження фізичних величин.

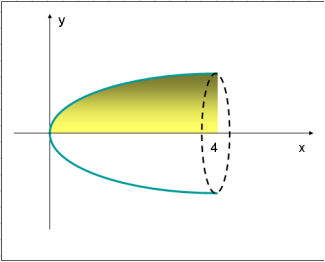
1. Знайти об’єм тіла обертання навколо осі абсцис фігури, обмеженої графіком функції            та прямими х = 4, у = 0.(8π).

2. Тіло рухається прямолінійно зі швидкістю   (м/с).

Обчислити шлях, який пройшло тіло:

а) за інтервал часу від  до (68 м)

б) від початку руху до зупинки ... (125 м).

3. Вантаж масою m = 3 кг розтягує пружину, підвищену вертикаль- 

но, на довжину l = 0, 04 м. Обчислити роботу, яка при цьому виконується.(1,2 Дж.).

4. Знайти масу стержня завдовжки 40 см, якщо його лінійна густина змінюється за законом ρ(l) = 3l+4

VI. Підсумок уроку.

Робиться підсумок зробленого за урок.

Учні відповідають на запитання, використовуючи технологію „Метод незакінчених речень”.

„На початку уроку я поставив перед собою мету ...”

„Цей урок мені запамятався тим, що ...”.

VII. Оголошення оцінок.

VIII. Домашнє завдання:

 

 Середній рівень.

1.Знайти загальний вигляд первісною для функції f(x) = x +6, .

2.Знайти площу фігуру обмеженої лініями , .

 

Достатній рівень.

1.Обчислити інтеграл ,  .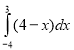

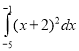2.Знайти площу фігури, обмеженої лініями    та віссю абсцис.

Високий рівень.

1.Використовуючи геометричний зміст інтегралу, обчислити:

1) 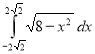;    2) .

2.Знайти об’єм тіла, утвореного обертанням навколо осі абсцис фігури, обмеженої:

косинусоїдою y = cos x та прямими х = 0, х = , у = 0.