Інтегрований урок. Тема: «Рівняння». 8 клас. Алгебра. Поглиблений рівень

 

 

 

 

 

 

Інтегрований урок

Тема: «Рівняння»

8 клас

Алгебра. Поглиблений рівень

 

 

Виконала: вчитель математики,

спеціаліст вищої категорії

Т. В. Федоренко

Алгебра 8 клас

Тема уроку: «Рівняння»

Мета уроку: узагальнити знання учнів про рівняння; продовжити

формування навичок розв’язування лінійних, квадратних та дробово-раціональних рівнянь; показати використання рівнянь в інших науках; сприяти вихованню всебічно розвинутої особистості, вихованню активної життєвої позиції; розвивати емоційну сферу учня.

Обладнання: портрети Евкліда, О. Хайяма, Ф. Вієта, Р. Декарта, М. І.

Лобачевського.

Хід уроку

I. Мотивація навчальної діяльності.

Учитель математики. Пропоную подивитися запропоновану вашими товаришами сценку «Секрет юного бізнесмена» і відгадати тему нашого уроку.

 

 

II. Постановка мети й завдань уроку.

Сьогодні на уроці мова піде про рівняння. Ми спробуємо узагальнити знання про ті види рівнянь, з якими вже знайомі.

III. Актуалізація опорних знань.

1. Що називається рівняння?

2. Що називають коренем рівняння?

3. Які види рівнянь ви вмієте розв’язувати?

 

Короткі виступи учнів

1. Лінійні рівняння.

Рівняння виду ax=b, де a, b – деякі числа, x – змінна, називається лінійним.

Лінійне рівняння має один корінь, коли a = 0;

Жодного кореня, якщо a = 0, b = 0;

Безліч коренів, коли a = b = 0.

Алгоритм розв’язування рівнянь, які зводяться до лінійних.

1. Розкрити дужки.

2. Перенести доданки зі змінною в один бік, числа – в інший, змінивши при цьому їх знак.

3. Знайти корінь, звівши подібні доданки.

Учні розв’язують такі рівняння:
 

а) 3x – 8 = x + 6; (x = 7)

б) (x – 7) – (2x + 9) = -13; (x = -3)

в) 0,8x – (0,7x + 0,36) = 7,1. (x = 74, 6)

 

2. Квадратні рівняння

Рівняння виду , де a, b, c – деякі числа (a0), x – змінна,

називається квадратним.

Формула дискримінанта та коренів.

При D > 0 – два корені –

;

D = 0 – один корінь – x

;

D < 0 – коренів немає.

a) зведене квадратне рівняння - ;

б) теорема Вієта ;

в) учні усно розв’язують рівняння:

 

1. .

2. .

3. .

Першим описав спосіб розв’язування лінійних рівнянь Хорезмі.

Абу Абдулла Абу Джафар Мухаммад ібн Муса аль-Хорезмі (біля 780 — біля 850)

Способи розв’язування квадратних рівнянь є у давньогрецьких учених Евкліда і Діофанта.

 

                                                  

Евклі́д (близько 365 — близько 270 до н. е.)                             Діофант Александрійський

                                                                                                   (між 200 та 214 — між 284 та 298) 

3. Дробово-раціональні рівняння.

Дробово-раціональне рівняння — це рівняння вигляду , де P(x), Q(x) – многочлени, а x – змінна.

Пригадаймо алгоритм їх розв’язування на прикладі:

1) Переносимо всі доданки в ліву частину, змінивши їх знаки:

2) Зводимо дроби до спільного знаменника:

3) Дріб дорівнює нулю, якщо чисельник = 0, а знаменник не дорівнює 0.

Складемо і розв’яжемо систему.

      

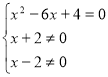
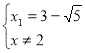
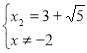
4) Виключимо з розв’язків ті, які перетворюють знаменник у 0.

Відповідь: ;

Розв’язати дробово-раціональне рівняння:

.

Розв’язання. , ОДЗ:

, 

–сторонній корінь, тому що не задовольняє вимогам ОДЗ. 

Відповідь. .

Учитель математики. Для чого потрібно розв’язувати рівняння? Так,

щоб за їх допомогою розв’язувати задачі. Рівняння називають мовою алгебри. Їх використовують не тільки в алгебрі, а й в інших науках, наприклад, в фізиці та хімії.

У фізиці. Розглянемо задачу: Тіло кинули вертикально вгору зі швидкістю 40 м/с. Через скільки секунд тіло буде на висоті 60 м?

Поглянувши на ми одразу впізнаємо квадратне рівняння.

60 = 40t-5t. Маємо квадратне рівняння:

-5t+40t-60=0

t- 8t + 12 = 0

За теоремою Вієта ;

 Отже, тіло опинилося на висоті 60 м два рази: через 2 секунди і через 5 секунд після кидання вертикально вгору.

У хімії. До розчину натрій сульфату масою 250 г з масовою часткою солі 15 % додали 50 г води. Обчисліть масову частку розчиненої речовини в новому розчині.

Дано: m1(розч.) = 250 г

m(H2O) = 50 г

ω1 = 15 %

ω2 - ?

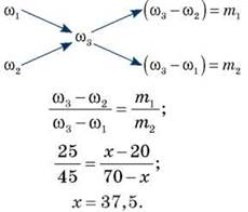
 Отже, відповідь: 37, 5%

Учитель математики. Різновиди рівнянь не вичерпуються тими трьома видами, які ми вміємо розв'язувати. Для математиків важливо було навчитися розв'язувати рівняння третьо­го порядку (кубічні).

Чи обмежуються всі види рівнянь третього порядку такими простими, чи є й інші і для їх розв'язування потрібні спеціальні способи розв'язування?

Першим, хто поставив це запитання і дав відповідь на нього, був видатний перський учений і поет Омар Хайям. Спробуємо створити портрет людини, яка запропонувала один із способів розв'язу­вання кубічних рівнянь — геометричний.

Народився Омар Хайям в 1048 р. в місті Нішапурі, шо на півдні від Ашхабада. Жив і працював у Самарканді, Бухарі, Ісфагані та інших містах Серед­ньої Азії та Ірану. Ми знайомі з його працею «Про доведення за­дач алгебри». Тут подано класифікацію, рівнянь 1-го, 2-го і 3-го порядків, стверджується, що алгебра — наука про знаходження невідомих за допомогою рівнянь.

Одним з методів розв'язування рівнянь Хайям пропонує геометричний. У цьому ідеї вченого про зв'язок алгеб­ри з геометрією нагадують світогляд за­сновника аналітичної геометрії Рене Декарта.

У 1077 р. Хайям закінчив ще одну математичну працю — «Коментарі до складних постулатів книги Евкліда», яка містила оригінальну теорію паралельних прямих. Хайям був придворним астрономом і радником султана Мелік-шаха. Він керував реформою календаря, зробив­ши його не місячним, а сонячним. Цей календар відрізняється від сучас­ного усього на 7 с. 

 

IV. Підсумок уроку.