Інтегрований урок з алгебри і хімії

Інтегрований урок з математики та хімії.

Тема: «Задачі на суміші та сплави».

Мета:

- актуалізувати поняття відсотка, масової частки речовини і концентрації речовини, сформувати навички прикладного використання апарату систем лінійних рівнянь, виявити рівень оволодіння учнів комплексом знань і умінь щодо вирішення завдань на суміші хімічними і математичними способами;

- розвивати здібності до самостійного вибору методу розв'язання задач, уміння узагальнювати, абстрагувати і конкретизувати знання, вміння оцінювати власні можливості;

- виховувати пізнавальний інтерес до хімії та математики, культуру спілкування, здатність до колективної роботи.

Тип уроку: удосконалення знань умінь і навичок.

Методи навчання, прийоми: математична розминка (фронтальне опитування),  хімічна розминка (фронтальне опитування), демонстраційний дослід, розв’язування задач (колективно, в парах, ), робота з листами «Удосконалення ЗУН»

Основні терміни і поняття: «відсоток», «суміш», «сплав», «розчин», «масова частка розчиненої речовини в розчині», «масова частка речовини у суміші».

Міжпредметні зв’язки: алгебра і початки аналізу: «Відсотки», «Система рівнянь»; хімія «Розв’язування задач на суміші та сплави».

Наочність:

• підручники «Хімія. 11 клас» (автори Савченко І.О., Крикля Л.С, Попель П.П), (15шт);
• підручники «Математика. 10 клас» (автори Г,П. Бевз, В.Г. Бевз), (15шт);
• міні-таблиця: періодична система хімічних елементів Д. І. Менделєєва (15шт);
• таблиця «Відсоткивий вміст речовини»;
• мультимедійний супровід уроку «Задачі на суміші та сплави».

Реактиви та обладнання: розчин купрум (ІІ) хлориду, дистильована вода; штатив для пробірок, пробірки, конічна колба, скляна паличка.

Технічні засоби навчання: комп’ютер, мультимедійний проектор, проекційний екран.

Хід уроку:

І. Організаційний етап.

Перевірка присутніх та готовності до уроку.

ІІ. Мотивація пізнавальної діяльності.

Викладач математики: Сьогодні у нас незвичайний урок, це інтегрований урок математики та хімії і вести його будуть два вчителі

На цьому уроці ми подивимося з вами на завдання з двох точок зору - з хімічної та математичної, і з'ясуємо: як математика допомагає у вирішенні хімічних задач і як хімія вирішує деякі математичні завдання.

Викладач хімії: У повсякденному житті, ми зможемо застосувати свої знання за рішенням подібних завдань, розбавляючи оцтову есенцію для домашніх заготовок, готуючи розчини для поливу ґрунтів на садовій ділянці, розраховуючи масу дорогоцінних металів в ювелірних прикрасах.

Організація здорового способу життя змушує нас частіше заглядати на упаковки продуктів харчування, щоб побачити процентний вміст різних речовин. Ми говоримо про екологію району, коли бачимо об'ємну частку газоподібних викидів підприємств і транспорту.

Тема уроку - Задачі на суміші та сплави.

Задачі:

• повторити і удосконалити знання з тем: «Відсоткові розрахунки», «Суміші і сплави»;
• порівняти хімічний і математичний спосіб розв’язування задач.

У кожного з вас є лист удосконалення ЗУН, який ви будете заповнювати протягом уроку, а вдома вклейте в робочі зошити. Протягом уроку ви збираєте собі фішки (додаткові бали) (одна фішка – один бал).

ІІІ. Актуалізація опорних знань та умінь.

Перед тим як перейти до теми нашого уроку давайте пригадаємо поняття, які нам сьогодні знадобляться.

Математична розминка

Згадаймо відсотки:

1. Знайти 30% від 4220
2. Скільки% складе 15 від 75?
3. Знайдіть число, 20% якого дорівнюють 12
4. Яке число, збільшене на 13% складе 226?
5. На скільки% чісло150 більше чісла120?
6. На скільки% число 120 менше числа 150?

Хімічна розминка

1. Що таке суміш?
2. Як можна класифікувати суміші?
3. Де ми зустрічаємо суміші?
4. Що таке сплави?
5. За якою формулою розраховується масова частка речовини?

ІV. Удосконалення ЗУН.

 

1. Демонстрація хімічного досліду.

У склянку з концентрованим розчином хлориду міді (II) зеленого кольору додається вода. Розчин стає блакитним.

Викладач хімії: Чому розчин змінив колір?

Пояснення: розчин змінив забарвлення через зміни масової частки хлориду міді в розчині.

 

2. Розв’язування задач на суміші речовин.

 

Задачі на складання рівняння.

Робота листами удосконалення ЗУН«Розв’язування задач на суміші та сплави».

Задача №1. Скільки г води було додано до 200 г 40% розчину купрум (ІІ) хлориду, якщо розчин став десятивідсотковим?

Викладач хімії:

Хімічне вирішення задачі (метод «стаканчиків»):

                           

 

             }200г}200+х

       (запис рівняння на дошці)

Викладач математики: Вирішуємо задачу математичним способом, перед цим згадуємо формулу:

  % Вміст = маса речовини / маса розчину * 100%:

Нехай х грам треба додати, х> 0, тепер складаємо таблицю:

	Маса розчину	% речовини	Маса речовини
Перший розчин	200	40 =0,4	0,4 * 200
Другий розчин	200 + х	10=0,1	0,1 * (х + 200)

Так як маса речовини не змінилася, можна скласти рівняння:

0,4 * 200 = 0, 1 * (х + 200)      (запис рівняння на дошці)

Таку ж таблицю ми будемо складати при вирішенні задач системою лінійних рівнянь.

 

Задачі на складання системи рівнянь.

Задача № 2. Є 2 посудини, що містять відповідно 4 і 6 кг розчину кислоти різних концентрацій. Якщо їх злити разом, то вийде розчин, що містить 35% кислоти. Якщо ж злити рівні маси цих розчинів, то вийде 36% розчин. Скільки кг кислоти міститься в кожному розчині?

Викладач математики: Спочатку розберемо математичних спосіб вирішення:

Нехай х кілограм маса речовини в першому розчині, у - кілограм маса речовини у другому розчині, 0 <x <4; 0 <y <6:

	Маса розчину	% вміст речовини	Маса речовини
Перший розчин	4	(х * 100)/4	х
Другий розчин	6	(у * 100)/6	у
Перший + другий раствор	10	35	0,35 * 10
Перший раствор	10	(х * 100)/4	х/4  * 10
Другий раствор	10	(у * 100)/6	у/6 * 10
Перший + другий раствор	20	36	0,36  * 20

Складаємо і розв'язуємо систему:

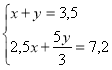      (запис рівняння на дошці)

Викладач хімії:

Хімічний розбір рішення:

Нехай ω в першій посудині - х%; ω у другому посудині - у%. Тоді маса чистої кислоти в 1 посудині-4х, у другому – 6у. Звідси масова частка:

або 4х +6 у = 3,5

Візьмемо за 1 кг кожного розчину (маси дорівнюють):

або х + у = 0,72

Вирішимо систему рівнянь:

      (запис рівняння на дошці)

 Відповідь: 1,86 кг; 1,64 кг.

 

3. Робота в парах «хіміки» та «математики».

Пропонуємо вам зараз перетворитись на дослідників «хіміків» і «математиків».

Ви об’єднанні в пари за партами, тому і працювати будете разом із сусідом. Ваше завдання:

• розв’язати запропоновану задачу хімічним або математичним методом.
• час виконання 5 хвилин.
• за правильне розв’язання ви отримаєте по 6б.

Кожна пара обирає свій спосіб вирішення.

Задача №3. У першому і другому сплавах мідь і цинк відносяться як 5:2 і 3:4. Скільки кожного сплаву потрібно взяти, щоб отримати 28кг нового сплаву з рівним вмістом міді і цинку?

Математичне вирішення:

	маса сплаву (кг)	маса міді (кг)	маса цинку (кг)
1 слиток	X	5/7 x	2/7 x
2 слиток	Y	3/7 y	4/7 y
1 + 2	28	14	14

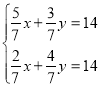
Хімічне вирішення:

Перший сплав: маса сплаву - х кілограм

ω_Cu =5/7 ≈ 0.71, m_Cu = 0.71 x кг

ω_Zn =2/7 ≈ 0.28, m_Zn = 0.28 x кг

Другий сплав: маса сплаву - у кілограм

ω_Cu =3/7 ≈ 0.43, m_Cu = 0.43 у кг

ω_Zn =4/7 ≈ 0.57, m_Zn = 0.57 у кг

m_{Cu =} m_Zn ; 0,71 x + 0.43 y = 0.28 x + 0.57 y,

тоді 0,43 х = 0,14 у; х : у = 3 : 1,

тому маса нового сплаву - 28кг, то маса першого сплаву - 21кг, а маса другого сплаву - 7кг.

Час закінчився.

• підніміть руки хто розв’язував хімічним? математичним методом?
• зараз обміняйтесь з опонентами аркушами і давайте перевіримо правильність виконання. Нагадую, що правильне розв’язування оцінюється в 6б, а далі в залежності з типом помилки, якщо виникнуть забруднення порадьтесь з викладачем

VІ. Інструктаж домашнього завдання.

Вирішити дані задачі двома способами:

1. Яку масу солі треба додати до 500 грам 10% розчину солі, щоб розчин став 25%?

2. Обчислити вагу і процентної вміст срібла в сплаві з міддю, знаючи, що, сплавивши його з 3 кілограмами чистого срібла, отримають сплав, що містить 90% срібла, а, сплавивши його з 2 кілограмами сплаву, що містить 90% срібла, отримають сплав 84% змісту срібла. (Відповідь: 2,4 кілограма і 80%).

VІІ. Підбиття підсумків уроку.

Тож що ми робили сьогодні на уроці? (відповідь учнів)

Викладач:

• ми удосконалили знання з теми : «Відсоткові розрахунки», «Суміші і сплави»;
• розглянули розв’язування задач з двох точок зору хімічної і математичної;

 

Виставлення та аргументування оцінок за урок.

Рефлексія.

Підводячи підсумки роботи, учні відповідають на питання:

1. Чи корисним для вас виявився цей інтегрований урок?

2. Чи змогли ви вибрати найбільш підходящий для вас спосіб вирішення?

3. Чи будете ви використовувати ці методи в подальшому і при вирішенні задач?

 

 

 

Лист удосконалення ЗУН.

з теми «Розв’язування задач на суміші та сплави».

Масова частка речовини розраховується за формулою:

 

 

 

Задача №1. Скільки г води було додано до 200 г 40% розчину купрум  (II) хлориду, якщо розчин став десятивідсотковим?

Дано:                               m1розч (CuCl2) = 200г    W1 (CuCl2) = 40% W2(CuCl2) = 10%          m2 (H2O) - ?

Хімічний розв’язок задачі:                                            }200г}…

Математичний розв’язок задачі:

  % Вміст = маса речовини / маса розчину * 100%:

Нехай х грам треба додати, х> 0, тепер складаємо таблицю:

	Маса розчину	% речовини	Маса речовини
Перший розчин
Другий розчин

Так як маса речовини не змінилася, можна скласти рівняння:

­­­­­­­­­­­­­__________________________________________________________________

Задача № 2. Є 2 посудини, що містять відповідно 4 і 6 кг розчину кислоти різних концентрацій. Якщо їх злити разом, то вийде розчин, що містить 35% кислоти. Якщо ж злити рівні маси цих розчинів, то вийде 36% розчин. Скільки кг кислоти міститься в кожному розчині?

Математичний розв’язок задачі:

Нехай х кілограм маса речовини в першому розчині, у - кілограм маса речовини у другому розчині, 0 <x <4; 0 <y <6:

	Маса розчину	% вміст речовини	Маса речовини
Перший розчин
Другий розчин
Перший + другий раствор
Перший раствор
Другий раствор
Перший + другий раствор

Складаємо і розв'язуємо систему рівнянь:

 

 

 

Хімічний розв’язок задачі:

Нехай ω в першій посудині - х%; ω у другому посудині - у%. Тоді маса чистої кислоти в 1 посудині-4х, у другому – 6у. Звідси масова частка:

 

 

Візьмемо за 1 кг кожного розчину (маси дорівнюють):

 

 

Вирішимо систему рівнянь:

 

 

Задача №3. У першому і другому сплавах мідь і цинк відносяться як 5:2 і 3:4. Скільки кожного сплаву потрібно взяти, щоб отримати 28кг нового сплаву з рівним вмістом міді і цинку?

Математичний розв’язок задачі:

	маса сплаву (кг)	маса міді (кг)	маса цинку (кг)
1 слиток
2 слиток
1 + 2

Хімічний розв’язок задачі:

Перший сплав: маса сплаву - х кілограм

ω_Cu =                , m_Cu =             

ω_Zn =                , m_Zn =

Другий сплав: маса сплаву - у кілограм

ω_Cu =                , m_Cu =

ω_Zn =                , m_Zn =

m_{Cu =} m_Zn ;                                                                     ,

тоді,

тому маса нового сплаву -      кг, то маса першого сплаву -     кг, а маса другого сплаву -                   кг.

Домашнє завдання. 1. Яку масу солі треба додати до 500 грам 10% розчину солі, щоб розчин став 25%?

2. Обчислити вагу і процентної вміст срібла в сплаві з міддю, знаючи, що, сплавивши його з 3 кілограмами чистого срібла, отримають сплав, що містить 90% срібла, а, сплавивши його з 2 кілограмами сплаву, що містить 90% срібла, отримають сплав 84% змісту срібла. (Відповідь: 2,4 кілограма і 80%).