Урок алгебри і початки аналізу в 10 класі.
Урок алгебри і початки аналізу в 10 класі.
Тема. Розв'язування найпростіших тригонометричних рівнянь.
Рівняння sinx=a, tgx=a, ctgx=a.
Мета. Засвоєння учнями виведення і застосування формул для
Знаходження коренів рівняння ( sint, tgt, ctgt ).
Розвиток мислення на основі синтезу і аналізу.
Виховання наполегливості, уважності.
Тип. Комбінований урок.
Урок алгебри і початки аналізу в 10 класі.
Тема. Розв’язування найпростіших тригонометричних рівнянь.
Рівняння sinx=a, tgx=a, ctgx=a.
Мета. Засвоєння учнями виведення і застосування формул для
Знаходження коренів рівняння ( sint, tgt, ctgt ).
Розвиток мислення на основі синтезу і аналізу.
Виховання наполегливості, уважності.
Тип. Комбінований урок.
Обладнання. Таблиці з опорними конспектами.
Епіграф. Вивчення математики подібне до Нілу, що починається
невеличким струмком, а закінчується великою річкою.
Ч. К. Колтон.
І.Актуалізація опорних знань.
1. Два учні біля дошки розв’язують рівняння (на повторення).
1.2cos(
-
)=
, 2.cos2x-1=0,
cos (
-
)=
, cos2x=1,
-
=
arccos+2πn, n
Z, 2x=2πn, n
Z,
-
=
+2πn, n
Z, x=πn, n
Z.
=
+2πn, n
Z, Відповідь: x=πn,n
Z.
x=
+4πn,n
Z.
Відповідь: x=
+4πn,nєZ.
2.Перевірка домашнього завдання (питання про забруднення).
Усно перевіряються відповіді з коментарями про використані при
розв’язанні тригонометричні тотожності:
№1. 5) x=
+πn,n
Z, ( особливий випадок),
9)x=
+2πn,n
Z,
10)x=
+
πn,n
Z,
13)x=
+2πn,n
Z.
№2 2)x=
+
,n
Z, (формула суми двох чисел),
4)x=
+πn,n
Z, (формула подвійного аргумента).
3.Перевірка раніше засвоєних знань ( методом фронтальної бесіди).
1.Область значень arccosa ( 
).
2.Які рівняння називаються тригонометричні?
3.Які тригонометричні рівняння називаються найпростішими ( sinx=a,
cosx=a, tgx=a, ctgx=a).
4.Які розв’язки має рівняння cost=a : 1)при 
1, ( Ǿ ),
2)при
1, формула
t=
arccosa+2πn,n
Z.
3)особливі випадки ( cost=0, cost=1, cost=-1).
4.Розглядаємо розв’язки на дошці ( питання?).
ІІ. Мотивація , повідомлення теми і мети уроку.
Ми розглянули формули для розв’язування найпростіших тригонометричних рівнянь виду cos t = a .
Наступне питання виведення і застосування формул для розв’язування тригонометричних рівнянь виду sin t = a .
1
-
якщо │а│> 1 , то рівняння не має розв’язків і я. │sin t│
1, для будь якого t .
- якщо │а│< 1 , то враховуючи , що sin t – ордината точки Рt одиничного кола , маємо :
ординату , рівну а, мають дві точки одиничного кола.
Рt2 a Pt1 ( на осі у відкладаємо т. а і проводимо 
до осі у
t2 t1 яке перетне коло в двох точках , які мають кути
t1 = arcsin a + 2πn, n є Z
t2 = π – arcsin a + 2πn, n є Z ці формули можна поєднати в вигляді однієї формули t = (-1)karcsin a + πk , k є Z.
т я. при k-парному маємо t1 , при k- непарному маємо t2 .
- Особливі випадки
а = 1 t = 
+ 2πn , n 
Z
a = -1 t = - + 2πn , n Z
a = 0 t = 0 +πn , t = πn , n Z .
Закріплення :
sin x = 
; sin x = - 
;
x = (-1)k
+ πk , k Z ; x = (-1)k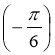
+ πk , k Z ;
x = (-1)k+1
+ πk , k Z ;
- Розглянемо рівняння виду .
tg t = a ( зручно розглянути за допомогою лінії тангенсів )
з якої видно що рівняння має один розв’язок при будь-яких а.
t = arctg a + πn , n Z , ( лінія котангенсів )
Рівняння ctg t = а , де а 
0
рівносильне рівнянню tg t = 
,
але ми маємо формулу і для ctgt=a,
t=arcctga+πn, n
Z.
ІІІ. Систематизація знань.
Розв’язати рівняння:
-
tgx=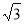, x=arctg
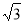+πn,n
Z,
x=
+πn,n
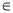Z.
2.tgx=2, x=arctg2+πn,n
Z, (обчислюємо калькулятором, або за
таблицями Брадиса).
3.3tg2x+2tgx-1=0, нехай tgx=y, тоді 3y2+2y-1=0
x1=1, x2=
,
звідси tgx=-1 або tgx=
x=-
+πn,n
Z, x=arctg+πn,n
Z.
Вчитель відповідає на запитання, яки виникли під час розв’язання
рівнянь.
ІV. Підведення підсумків.
1.Розглянули формули для розв’язування найпростіших тригонометричних рівнянь.
2.Записали опорні конспекти (вивчити).
3.Домашнє завдання.
про публікацію авторської розробки
Додати розробку