Інтелектуальна гра для учнів 5,6,8 класів "Математичне поле чудес"

Інтелектуальна гра з математики

для учнів 5,6,8 класів

«Математичне поле чудес».

Мета: сприяти подальшому розвитку пізнавальних здібностей учнів; підвищувати інтерес до математики та історії її розвитку; формувати активну життєву позицію, уміння відстоювати свою точку зору; створювати умови для самореалізації учнів у процесі підготовки до гри; розвивати інтелектуальний рівень; дати можливість кожному учневі виявити активність, показати рівень своєї підготовки й ерудиції; сприяти розвитку навичок міжособистісного спілкування; виховувати цікавість до предмету, терплячість, наполегливість.

Форма: Інтелектуальна гра.

Учасники:

І Трійка:  три учні з 5 кл.

ІІ Трійка: три учні з 6 клас.

ІІІ Трійка: три учні з 8 клас.

Обладнання та реквізити: барабан зі стрілкою, що обертається, на якому є числа – кількість очок; літера «П» - приз; літера «Б» - банкрут; знак «+» - право відкрити букву;ноутбук; флешка із музикою з гри « Поле чудес», скринька, призи;

Педагогічні можливості заходу: матеріал заходу може використовуватись як додатковий історичний при вивченні відповідних тем .

Підготовчий етап:

1. жеребкуванням визначаємо по 3 учні з кожного класу, які будуть приймати безпосередню участь в грі;
2. на початку тижня вивісила стінгазету з цікавими відомостями про математику і запропонувала учням ознайомитися з додатковою літературою з історії математики;
3. На початку гри треба повідомити гравцям, що за три поспіль відгадані букви вони отримують можливість вибрати одну з двох скриньок: одна з призом, друга порожня; ознайомити з усіма секторами барабана.

Хід гри.

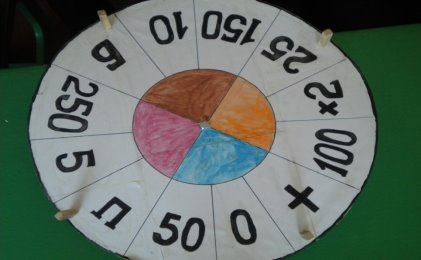
Ведучий запрошує на сцену першу трійку учасників, які під музику займають місця біля барабана. Після презентації кожного гравця учасники отримують завдання.

Завдання для першої трійки.

Сторона прямокутника.

Гравці відгадують букви й слово так, як це відбувається у відомій грі «Поле чудес». Якщо у когось на барабані випадає сектор «П» , він отримує приз і вибуває з гри, якщо відмовляється від призу, то продовжує гру.

Якщо гравець  поспіль вгадав три букви, то отримує можливість вибрати одну з двох скриньок : одна з призом; друга – порожня.

Після того як визначився переможець першої трійки й усі члени трійки зайняли свої місця в залі, ведучий пропонує глядачам узяти участь у грі  й теж отримати приз, якщо їхня активність буде гідна винагороди.

Гра з глядачами.

Пропонуємо глядачам задачі на кмітливість.

1. Жінка, ідучи до Києва, зустріла трьох чоловік. Кожний із них ніс мішок, а в кожному мішку – по коту. Скільки живих істот ішло до Києва? ( Відповідь: тільки жінка.).
2. Трійка коней проїхала за годину 15 км. З якою швидкістю скакав кожний кінь?

     ( Відповідь: 15 км/год.)

3. Назвіть найбільше чотирицифрове число, сума цифр якого дорівнює трьом.

( Відповідь: 3000.)

Ведучий запрошує вийти на сцену другу трійку гравців і рекомендує їх.

Завдання для другої трійки

Цей термін увів у 17 ст. французький математик Ф. Вієт. У перекладі з латинської він означає «спиця колеса». Що це?

Гра другої й третьої трійки проходить за аналогією до гри першої трійки.

Гра з глядачами.

Пропонуємо пограти в гру « Не скажу». Ведучий та кілька глядачів по черзі називають числа від 1 до зо. При цьому числа, які кратні трьом називати не можна. Замість них слід вимовляти «не скажу». Той, хто помилився, вибуває. Перемагає останній гравець, який залишився у грі.

Ведучий. До залу запрошується третя трійка гравців.

Завдання для третьої трійки

Один із перших учених-математиків, який жив у VІ столітті до нашої ери в Стародавній Греції. У молодості він багато подорожував, відвідав Єгипет і Вавилон. Саме він відкрив властивості кутів рівнобедреного трикутника, установив, що діаметр поділяє коло на дві рівні частини. Він є автором добре відомої вам теореми. Його ім’я складається з п’яти літер.

Гра з глядачами.

Пропонуємо узяти участь у грі « Кожній руці – своє діло» : правою рукою слід малювати цифру 9, а лівою водночас – 6. Викликаємо три глядача і вони виконують на дошці.

Фінальна гра.

Для участі у фінальній грі ведучий запрошує на сцену п’ятьох  фіналістів.

Завдання для фінальної гри.

Книги цієї людини мали трохи менший вклад, ніж Біблія. Довгий час її праці були майже єдиним шкільним посібником одного з розділів математики. Це вона мала сміливість відповісти цареві: «У математики немає царського шляху». Назвіть ім’я цієї людини.

Супергра.

(суперприз:  поточна оцінка з математики 12 балів)

Ведучий пропонує переможцеві взяти участь у супергрі.

Завдання для супергри.

Яке геомотричне тіло зображене на банкноті в 1 доллар США

Підбиття підсумків гри.

1. Привітання переможця.
2. Вручення призів.
3. Визначення переможця гри за кількістю очок набраних під час гри.

Ведучий. Дякую всім учасникам сьогоднішньої гри за активність і сподіваюсь, що ви багато нового й цікавого дізналися з історії математики.