Інтерактивні методи навчання на уроках математики
1.Інтерактивні методи навчання на уроках математики…………………………………………………………5
1.1 Класифікація інтерактивних методів навчання…………………..5
1.2 Технології інтерактивного навчання на уроках математики…...9
1.3 Використання проектної технології в роботі вчителя матема-
тики………………………………………………………………...16
1.4 Правила організації інтерактивного навчання……………….....21
1.5 Застосування інтерактивних методів навчання……………........22
2.Додатки
2.1. Конспект уроку „Перпендикулярність прямих і площин ”
(бізнес-гра)10клас.……………………………………………………25
2.2Конспект підсумкового уроку з теми „ Десяткові дроби ”
(метод проектів)5 клас .…………………………………………… 29
2.3 Урок «Подорож геометричною країною» 5 клас………………36
2.4 Конспект уроку з теми «Дії з натуральними числами» (урок-подорож) 5клас………..………………………………………………40
Відділ освіти Сколівської РДА
Сколівська академічна гімназія
„Інтерактивні методи навчання на уроках математики”.
Сколе
Зміст
Вступ……………………………………………………………3
- Інтерактивні методи навчання на уроках математики…………………………………………………………5
1.1 Класифікація інтерактивних методів навчання…………………..5
1.2 Технології інтерактивного навчання на уроках математики…...9
1.3 Використання проектної технології в роботі вчителя матема-
тики………………………………………………………………...16
1.4 Правила організації інтерактивного навчання……………….....21
1.5 Застосування інтерактивних методів навчання……………........22
- Додатки
2.1. Конспект уроку „Перпендикулярність прямих і площин ”
(бізнес-гра)10клас.……………………………………………………25
- Конспект підсумкового уроку з теми „ Десяткові дроби ”
(метод проектів)5 клас .…………………………………………… 29
2.3 Урок «Подорож геометричною країною» 5 клас………………36
2.4 Конспект уроку з теми «Дії з натуральними числами» (урок-подорож) 5клас………..………………………………………………40
- Висновки…………………………………………………............44
- Література………………………………………………………....46
Вступ.
Те, що я чую, я забуваю.
Те, що я бачу, я пам'ятаю.
Те, що я роблю, я розумію. (Конфуцій)
Сучасний школяр дуже не виразно уявляє межі своєї інформативності, а межі пізнання наук зовсім йому не відомі. Звідкіля ж тоді взятися допитливості, без якої будь-яке навчання лише виховання виконавців. Головне надбання школи — це не сума вкладених в голову відповідей на стандартний перелік питань. Виправданим і привабливим видом жадібності можна назвати жагу пізнання і саморозвитку. Щоб знання перетворювалися на інструментарій учень має з ними працювати. Поки вивчення і повторення здійснюється в режимі заучування, поки перевіркою знань вважається відповідь-переказ, школа працює на 90% даремно.
Що означає працювати зі знаннями? Це означає їх застосовувати, шукати умови на межі придатності, перетворювати, розширювати і доповнювати, знаходячи нові зв'язки та співвідношення, розглядати в різних моделях і контекстах.
Суть інтерактивного навчання в тому, що освітній процес відбувається за умови постійної, активної взаємодії всіх учнів
Інтерактивне навчання (з англ.)— це, по-перше, учіння, яке ґрунтується на взаємодії, по-друге, навчання, побудоване на взаємодії. Таким чином, основою інтерактивного навчання є взаємодія.
Взаємодія в освітньому процесі здійснюється у формі педагогічного спілкування, що розглядається як рівноактивна взаємодія — діалог. Діалектика педагогічного спілкування — міжсуб'єктної взаємодії — це розвиток процесів уподібнення та відокремлення суб'єктів спілкування. Міжсуб'єктна взаємодія — діалог — спонукає учасників до особистісного розвитку, самовизначення, персоналізації, соціального ототожнення, інтеграції. За слушним зауваженням М.Бахтіна, «тільки в спілкуванні, у взаємодії людини з людиною розкривається «людина в людині». Коли діалог закінчується, усе закінчується».
Отже, педагогічне спілкування можна визначити як діалог (полілог) на полімодульних рівнях (учитель — учень, учитель — учитель, учитель — навколишній світ, учень — навколишній світ) у цілісному співбутті суб'єктів освітнього процесу.
У ситуації діалогу учасники створюють, насамперед, цілісне психолого-педагогічне спільне буття — співбуття. Водночас діалог є універсальним засобом і принципом організації людської свідомості («інтрасуб'єктний план»).
Таким чином, основою інтерактивного навчання є взаємодія учасників процесу навчання що здійснюється за допомогою методів, які активізують педагогічне спілкування — діалог.
- Інтерактивні методи навчання на уроках математики
Інтерактивні методи навчання — це система способів діалогічної взаємодії суб'єктів навчання спрямованих на осмислення діалогу, його «інтер»-«інтра»-«мета»-суб'єктні плани.
1.1 КЛАСИФІКАЦІЯ ІНТЕРАКТИВНИХ МЕТОДІВ НАВЧАННЯ (ІМН)
ІМН можна класифікувати за кількома ознаками. Слушна, скажімо, класифікація дослідника М.В.Кларіна, в основу якої покладено принцип активності. Науковець пропонує методи фізичної, соціальної, пізнавальної активності. Так, прикладами фізичної активності є зміна робочого місця, запис, малювання тощо. Учасники включені в соціальну активність тоді, коли ставлять запитання, відповідають тощо. Приклади пізнавальної активності: доповнення учасниками викладеного матеріалу, виступ як джерело професійного досвіду, самостійний пошук розв'язання проблеми. Звичайно, всі три види активності взаємопов'язані.
Віддаючи належне даному підходу, пропонуємо класифікувати ІМН, ураховуючи ключовий принцип такого навчання, а саме взаємодії — діалогу. Визначені дослідником О.В.Киричуком концептуальні підходи до педагогічного спілкування — діалогу, зокрема до механізмів його здійснення та основних функцій, можуть слугувати основою класифікації. На думку вченого, механізми спілкування (сприйняття — пізнання — оцінювання — вплив) розглядаються як форми реалізації його основних функцій: інформаційної, пізнавальної, мотиваційної та регулятивної. Відтак, ІМН спрямовується на реалізацію окремих функцій педагогічного спілкування — діалогу.
- Інформаційні ІМН на уроках математики.
Це способи діалогічної взаємодії учасників навчання з метою обміну матеріальними або духовними цінностями.
Ось деякі ідеї, що можуть зреалізувати ці методи на початку уроку.
«Перше знайомство». Учасники працюють у парах. Перш ніж назвати своє ім'я, слухачам пропонується подивитися один на одного і всміхнутися.
«Іменні жетони». Учасники готують особисті жетони за допомогою підготовленого викладачем матеріалу (папір, клей, ножиці, стрічки тощо). На жетонах пропонується подати характерологічну інформацію (професійне спрямування чи особистісні уподобання).
«Мандруємо разом». Слухачам дається нитка. Кожен учасник по черзі «подорожує» пальцями вгору і вниз, називаючи своє ім'я і розповідаючи щось цікаве про себе. «Мандри» припиняються тоді, коли всі учасники назвуть себе і розкажуть цікаву історію з власного життя.
Пізнавальні ІМН на уроках математики.
Це способи пізнавальної взаємодії (діалогу) учасників з метою отримання нових знань, їх систематизації, творчого вдосконалення професійних умінь і навичок.
До цих методів можна віднести:
Ділова гра — це форма відтворення предметного і соціального змісту, професійної діяльності спеціаліста, моделювання відносин, характерних для цієї діяльності як цілого. У грі за допомогою знакових засобів (мова, мовлення, графіки, таблиці, документи) відтворюється професійна обстановка, подібна за сутнісними характеристиками до реальної.
Пізнавальні інтерактивні методи включають і евристичні методи навчання. Загалом, на сьогодні визначення евристики сягає в кілька площин: по-перше, як спеціальні методи розв'язування задач (евристичні методи), які, як правило, протиставляються формальним методам розв'язування, що ґрунтуються на точних математичних моделях.
Навчальна евристична діяльність — це діяльність, у ході якої цілеспрямовано розвиваються здібності:
- розуміти шляхи та методи продуктивної навчально-пізнавальної діяльності, творчо копіювати їх та навчатися на своєму і запозиченому досвіді;
- систематизувати, тобто впорядковувати навчальну інформацію в інтеграційні комплекси, з метою оперування нею в евристичному пошуку;
-
адаптуватися до різноманітних видів навчальної діяльності,
передбачати її результати; - планувати й прогнозувати інтелектуальну діяльність на основі логічних операцій.
Евристичний метод.
«Мозкова атака» як один із системних методів пошуку ефективний в активізації колективної творчої діяльності. Відомо, що навчальний процес, який ґрунтується на критиці, створює фрустрації, гальмує мислення, творчі процеси людини. Щодо цього в психоаналітичних студіях З.Фрейда та в неофрейдистів є промовисте спостереження: «зустріч кожної людини з проблемною ситуацією ніколи не позбавлена відчуття страху, адже йдеться про те, що слід полегшити усталене, узвичаєне існування та увійти в смугу незвичайного, невідомого, непередбачуваного». Натомість у «мозковій атаці» пропонується розмежовувати процеси формулювання гіпотез та їх критичне оцінювання. При цьому означені процеси здійснюються різними людьми.
Вчитель вимагає виконання правил «мозкової атаки»:
- Умови задачі формулюються у загальних рисах перед «атакою».
- Група «генераторів ідей» пропонує максимальну кількість гіпотез за відведений час (20хв). Висуваються будь-які гіпотези: фантастичні, помилкові, жартівливі. Регламент на кожну ідею — у межах 2 хв (без доведень). Усі ідеї записуються. На цьому етапі забороняється будь-яка критика. Підвищити активність «мозкової атаки» можна через релаксацію, що дасть змогу зняти психічне й м'язове навантаження.
-
Група експертів оцінює запропоновані гіпотези. Експертиза та
відбір гіпотез проводяться ретельно, оцінюються несерйозні та нереальні гіпотези. - Нерозв'язана в процесі «атаки» задача може бути запропонована цьому самому колективу, але в дещо видозміненій формі.
- Активізувати процес генерування ідей рекомендується за допомогою таких прийомів як інверсія (зроби навпаки); аналогія (зроби так, як це зроблено в попередньому розв'язанні); емпатія (вважай себе частиною задачі, з'ясуй при цьому свої відчуття).
-
Гіпотези оцінюються за десятибальною системою, за оцінками
всіх експертів виводиться середній бал.
Синектичннй метод.
До системних методів активізації розумової діяльності та інтерактивного навчання належить синектичний метод. Синектика (гр. — поєднання різнорідних елементів) — система методів інтенсивної психологічної активізації процесів знаходження розв'язків проблеми. Методика є логічним розвитком «мозкової атаки». Відмінність їх лише в тому, що остання проводиться з людьми, які не мають досвіду творчої діяльності. Синектика передбачає створення постійних груп, які в процесі своєї діяльності нагромаджують досвід, різноманітні прийоми.
Оптимальна кількість учнів у групі — 5—7 осіб. Протягом декількох місяців групу готують до роботи.
- Мотиваційні ІМН.
Це способи діалогічної взаємодії учасників навчального процесу, за допомогою яких кожен визначає власну позицію у ставленні до способів діяльності групи, окремих учасників, викладача, самого себе. Серед цих методів можна назвати такі:
«Мої очікування». Слухачі на мотиваційному етапі заняття (або на діагностичному етапі курсового навчання) визначаються за такими напрямами:
Я очікую від себе...
...від колег...
.. .від вчителя...
Пропонується висловити очікування на початку і в кінці заняття.
«Лист до самого себе». Слухачі пишуть лист самі до себе, у якому перелічують усе, що вони мають намір зробити за результатами заняття. Лист кладуть у конверт, адресований собі. Через чотири-шість тижнів після заняття лист надсилають. Це буде ввічливе нагадування самому собі від себе учасника.
«Самооцінка». Учасники класифікують позитивне-негативне в організації та проведенні заняття. Наступне заняття бажано розпочати з коментаря щодо покращення роботи (відповідно до названих слухачами недоліків).
«3:2:1». Учасники визначають:
• 3 положення, які дійсно їх зацікавили на занятті;
- 2 положення, які хотілося б поглибити;
-
1 положення, яке вони будуть використовувати в практичній
роботі.
«Інтерв'ю». Учасники працюють у парах, ставлять запитання, які актуалізують знання з темами, що вивчається. Наприклад:
- Що Ви знали із цієї теми?
- Які запитання із цієї теми у Вас виникли?
Наступним кроком є обговорення відповідей на запитання інтерв'ю.
- Регулятивні ІМН.
Це способи, завдяки яким встановлюються та приймаються певні правила діалогічної взаємодії учасників навчання. Наведемо деякі ідеї, зокрема:
«Виробимо правила». Перед заняттям слухачі формулюють і записують правила, якими керуються упродовж навчання. Ці правила можуть доповнюватися, змінюватися. Формулюючи їх, бажано уникати негативних тверджень:
- правило піднятої руки;
- говорити першим;
- право на помилку тощо.
1.2 Технології інтерактивного навчання на уроках математики.
- Технології кооперативного навчання.
Парна і групова робота організовується як на уроках засвоєння, так і на уроках застосування знань, умінь і навичок. Це може відбутися одразу ж після викладу вчителем нового матеріалу на початку нового уроку замість опитування, на спеціальному уроці, присвяченому застосуванню знань, умінь та навичок, або бути частиною повторювально-узагальнюючого уроку.
Робота в малих групах( „діалог”, „синтез думок”, ”спільний проект”, „коло ідей”) — більшість завдань виконуються в малих групах або в парах. Ця форма організації корисна для формування навичок участі в дискусії. Більшості учнів легше висловитися в невеличкій групі, до того ж цей метод дає можливість заощадити час, бо відпадає потреба вислуховувати кожну дитину у великій групі. Заняття в малих групах дає змогу учням набути навичок, необхідних для спілкування та співпраці. Дискусії малими групами стимулюють роботу в команді, розвивають почуття терпимості та поваги до думки інших. Об'єднувати учнів у групи можна різними способами:
- роздати дітям геометричні фігури;
- розділити за порами року;
- розділити за кольором розданих матеріалів.
Як організувати роботу?
Об'єднайте учнів у групи. Почніть із груп, що складаються з трьох учнів. П'ять-шість учасників — це оптимальна верхня межа для проведення обговорення в малій групі.
Повідомте учнів про ролі, які вони мають розподілити між собою й виконувати під час групової роботи.
Спікер, головуючий: зачитує завдання групі, організовує порядок виконання, пропонує учасникам висловитися по черзі, підбиває підсумки роботи, визначає доповідача.
Секретар: веде записи результатів роботи.
Посередник: стежить за часом, заохочує групу до роботи.
Доповідач: чітко висловлює думку групи.
Вчитель: повинен поставити кожній групі конкретне завданняі дати чітку інструкцію групової роботи.
Карусель
Цю технологію застосовують:
- для збирання інформації з певної теми;
- для інтенсивної Перевірки обсягу й глибини наявних знань;
- для розвитку вмінь аргументувати власну позицію.
Як організувати карусель?
Розставте стільці для учнів у два кола. Учні, які сидять у внутрішньому колі, розташовані спиною до центру, а ті, які сидять у зовнішньому обличчям до них. Таким чином, кожен сидить навпроти іншого.
Внутрішнє коло нерухоме, зовнішнє рухливе: за сигналом ведучого всі його учасники пересуваються на один стілець праворуч і опиняються перед новим партнером. Мета: пройти все коло, виконуючи поставлене завдання.
Акваріум
Ще один варіант кооперативного навчання, що є формою діяльності учнів у малих групах.
Як організувати акваріум?
Учитель об'єднує учнів у групи по 4-6 учасників і пропонує їм ознайомитися з завданнями.
Одна із груп сідає в центрі класу. Ця група отримує завдання для проведення групової дискусії.
Поки діюча група займає місце в центрі, учитель знайомить решту класу із завданням і нагадує правила дискусії у малих групах. Групі пропонується вголос, упродовж 3-5 хвилин обговорити можливі варіанти розв'язання проблемної ситуації. Учні, які перебувають у зовнішньому колі, слухають, не втручаючись у перебіг обговорення.
По завершенні відведеного для дискусії часу група повертається на свої місця, а учитель ставить класу запитання:
- чи погоджуєтесь ви з думкою групи?
- чи була ця думка достатньо аргументованою, доведеною?
Така бесіда може тривати 2-3 хвилини. Після цього місце в «Акваріумі» займає група, котра обговорює наступну ситуацію.
Наприкінці учитель має обговорити з учнями перебіг групової роботи, прокоментувати міру володіння навичками дискусії у малих групах.
- Технології колективно-групового навчання.
«Мозковий штурм» — це ефективний метод колективного обговорення, пошук рішень шляхом вільного висловлювання думок усіх учасників і допомагає знаходити кілька рішень з конкретної теми.
Вчитель на уроці називає проблему, яку треба розв'язати, та запрошує учнів взяти участь в її обговоренні шляхом колективного обдумування — «мозкового штурму», який організовується за такими етапами:
-
Обрану проблему записують на дошці або на папері, щоб під час
роботи цей запис був перед очима.
- Всі учасники пропонують ідеї щодо розв'язання висунутої проблеми.
- Ідеї записують на дошці.
-
Після того як майже всі ідеї зібрано, їх групують, аналізують,
розвивають групою. -
Вибирають ті ідеї, що, на думку групи, допоможуть вирішенню
поставленої проблеми.
Під час «мозкового штурму» найбільш ефективними правилами поведінки є такі:
-
намагайтеся зібрати якомога більше ідей щодо вирішення задачі
або проблеми; - слід примусити працювати уяву учнів, не відкидаючи жодної ідеї;
- можна подавати кілька ідей або розвивати ідеї інших;
—не можна обговорювати і критикувати ідеї інших, давати їм оцінку.
Робота у великій групі (тобто з усім класом) — навчальний метод, коли вся група обговорює ідеї чи події, що стосуються певної теми. Дуже важливо на уроках залучати до роботи всіх учнів. У цьому допомагає такий метод як «мікрофон». Учні по черзі імітують «говоріння в мікрофон». Інші діти не можуть говорити, вигукувати з місця, право говорити належить тільки тому, у кого символічний мікрофон.
- Технології ситуативного моделювання.
На сучасному етапі розвитку освіти в Україні першочергового значення набуває проблема методики розвитку школярів.
Це ставить нові вимоги до організації навчально-пізнавальної діяльності учнів, потребує застосування більш активних форм навчання.
Практика показує, що такими формами є інтерактивні технології. У сучасному суспільному житті ми спостерігаємо дебати партій, політиків, ток-шоу з відомими діячами, презентації фірм, дискусії перед мікрофоном, різні реклами тощо. Елементи таких заходів уплітаються в сучасний урок. Це не є штучним перенесенням модних форм соціального та політичного життя в навчальний процес. Інтерактивні форми на уроках — це веління часу. Новітні підходи до організації навчання роблять навчально-виховний процес різноманітним, цікавим та ефективним.
Під час проведення уроків математики та позакласних заходів використовуємо такі форми інтерактивних технологій, як презентація, реклама, мікрофон, ток-шоу, робота групами, парами, незакінчені речення, спільні проекти, мозковий штурм, рольова гра тощо.
Модель навчання у грі – це побудова навчального процесу за допомогою включення учня у гру.
Як правило, ігрова модель навчання мас чотири етапи:
-
орієнтація (введення учнів у тему, ознайомлення з правилами гри,
загальний огляд її перебігу); -
підготовка до проведення гри (ознайомлення зі сценарієм гри,
визначення ігрових завдань, ролей, орієнтовних шляхів розв'язання
проблеми); -
основна частина — проведення гри;
4) обговорення.
Метод реклами
Він зацікавлює учнів своєю новизною, сучасністю. Адже вони бачать, яке велике значення в житті має реклама. Користуючись цим прийомом, часто даємо учням завдання підготувати рек ламу про якесь математичне поняття, застосування якоїсь теми та ін. А на уроці «йде трансляція» реклами.
Наприклад, в 11 класі під час повторення теми «Рівняння» учням було дано завдання скласти рекламу про рівняння. Наведемо зразки.
Реклама 1
Вони допомогли фізикам відкрити елементарні частинки та античастинки. Використавши їх, Максвелл теоретично довів існування електромагнітних хвиль.
За їх допомогою у 1867 році «оживили» трансатлантичний кабель, що після першої спроби з'єднати Європу та Америку не працював.
Вони — це рівняння. Якщо ви хочете пов'язати своє життя з наукою, вивчайте рівняння.
Реклама 2
Вам треба дізнатися, яку швидкість повинен мати корабель, щоб до початку шторму вчасно прийти в порт?
Ви хочете розрахувати, за скільки днів сім гномів збудують терем для Білосніжки?
Вам треба визначити, скільки добрив треба внести для підвищення урожайності поля?
Тоді дружіть з рівняннями! Вони допоможуть вам розв'язати багато практичних проблем.
Приклад реклами «Інтеграл»
За його допомогою можна знайти шлях, пройдений матеріальною точкою; обчислити об'єм тіла обертання, площу фігури; знайти кількість електрики, змінну роботу. Все це може зробити його Величність інтеграл!
Тож глибше знайомтесь з темою «Застосування інтеграла».
Метод презентації
Його можна використовувати на уроці будь-якого типу. Часто доцільно застосовувати під час повторення вивченого матеріалу Учні вже багато знають про питання, що розглядається, том можуть цілісно, зв'язно і цікаво розповісти про нього.
Наведемо зразок презентації, запропонованої учнями.
Урок алгебри в 7 класі.
Тема. Рівняння
Мета: узагальнити знання учнів про рівняння.
Кожен учень готує презентацію-розповідь про те, що він знає про рівняння. Вчитель ставить перед учнями завдання: «Ви презентуєте «рівняння» перед слухачами аудиторії, яка про них мало що або навіть нічого не знає. Як ви це зробите?»
Група учнів або один учень виступає зі своєю презентацією. Ось одна із презентацій, наведених учнями.
Рівняння — це рівність, яка містить невідомі числа, позначені буквами.
Число, яке перетворює рівняння у правильну рівність, є його коренем.
Розв'язати рівняння — означає знайти його корені або показати, що їх не існує.
Рівняння може мати один корінь, два, ... безліч або зовсім не мати коренів. Є рівняння рівносильні. Це такі рівняння, які мають однакову множину розв'язків або зовсім їх не мають.
Під час розв'язування рівнянь треба знати властивості, які не порушують їх рівносильності: у рівнянні можна зводити подібні доданки; у рівнянні можна розкривати дужки, згідно з правилами.
Під час розв'язування рівнянь обидві його частини можна множити або ділити на відмінне від нуля однакове число.
Доданки рівняння можна перенести з однієї частини в іншу, змінюючи при цьому знаки.
Рівняння використовуються під час розв'язування багатьох практичних задач.
Рівняння були відомі багато століть тому.
Метод проектів
Пріоритетним напрямом реформування освіти є досягнення якісно нового рівня у вивченні базового навчального предмета — математики. Математичні знання і вміння розглядаються не як самоціль, а як засіб розвитку особистості школяра, забезпечення його особистої грамотності, як здатність розуміти роль математики у світі, в якому він живе, висловлювати обґрунтовані математичні судження і використовувати математичні знання для задоволення пізнавальних і практичних потреб. Відчути свою спроможність, успішність, комфортність на уроці дає використання сучасних технологій, а саме — проектної. Сучасна назва — проект, уже підвищує інтерес учнів до вивчення математики.
Метод проектів має велике значення для розвитку життєвої, соціальної, інформаційної, предметної компетентностей учня.
Метод дозволяє:
- перевірити та закріпити на практиці теоретичні знання;
- забезпечити продуктивний зв'язок теорії та практики у процесі навчання;
- набути життєвого досвіду;
- розвивати вміння аналізувати, систематизувати, узагальнювати вивчений матеріал;
- здійснювати організовану пошукову, дослідницьку діяльність на підставі спільної праці учнів;
- навчити учнів самостійно працювати з додатковою літературою;
- вчити вміння самостійно працювати над творчими завданнями;
- підвищувати інтерес учнів до вивчення математики;
- виховувати повагу, вміння працювати в колективі;
- формувати власну життєву позицію.
- Технології навчання у дискусії.
Дискусія надає чудову нагоду виявити різні позиції з певної проблеми або суперечливого питання. Щоб дискусія була відвертою, необхідно створити у класі атмосферу довіри та взаємоповаги.
Правила ведення дискусії:
- говоріть по черзі, а не всі одночасно;
- не переривайте того, хто говорить;
- критикуйте ідеї, а не того, хто їх висловлює;
- поважайте всі висловлені думки;
- не смійтеся, коли хтось говорить;
- не змінюйте тему дискусії;
- намагайтеся заохочувати до участі в дискусії інших,
Метод «Прес» можна використовувані у випадках, коли виникають суперечливі питання і потрібно зайняти і чітко аргументувати визначену позицію з проблеми, переконати інших у правильності своєї думки.
- Щоб бути чітким та переконливим, ваше висловлювання повинно мати таку структуру і етапи: Позиція: почніть зі слів «_Я вважаю, що...» та висловіть свою думку, поясніть, у чому полягає ваша точка зору.
-
Обґрунтування: починаючи словами «... тому, що...», наведіть
причину появи цієї думки, тобто поясніть, на чому ґрунтуються докази
на підтримку вашої позиції. -
Приклад: продовжуйте висловлювання словом «... наприклад...»
та наведіть факти, дані, що підтверджують вашу позицію. -
Висновки: закінчіть висловлювання «отже (тому), я вважаю...»
і узагальніть свою думку, зробіть висновок про те, як необхідно діяти.
Навчаючи — вчуся («Броунівський рух»)
Цей метод надає учням можливість взяти участь у навчанні та передачі своїх знань іншим. Робота організовується таким чином:
-
повідомивши тему та мсту уроку, роздати учням картки із
завданням-інформацією, яку вони повинні засвоїти; -
якщо учням щось не зрозуміло, то вони можуть звернутися до
вчителя; -
учні, підготувавшись до передачі цієї інформації, ознайомлюють
зі своєю інформацією однокласників; -
після передачі всієї інформації учні розповідають, про що вони
дізналися від інших.
Ажурна пилка
Такий вид діяльності на уроці дає можливість працювати разом, щоб вивчити значну кількість інформації за короткий проміжок часу, а також заохочує учнів допомагати один одному вчитися, навчаючи.
Під час роботи за допомогою методу «Ажурна пилка» учні повинні бути готовими працювати в різних групах.
- Спочатку учень працюватиме в «домашній» групі.
-
Потім він в іншій групі буде виступати в ролі експерта з питання,
над яким він працював в «домашній» групі та отримає інформацію від
представників інших груп. -
В останній частині заняття учень знову повернеться в свою
«домашню» групу, для того щоб поділитися тією новою інформацією,
яку йому надали учасники інших груп.
1.3 Використання проектної технології в роботі вчителя математики.
Усе, що я пізнаю, я знаю, для чого це мені потрібно, де і як я можу ці знання застосувати.
В. Кильпатрик
Проект (латиною projektus) означає буквально «кинутий уперед», із французької перекладається як «наміри, що здійсняться в майбутньому».
У педагогіці проект — це самостійна творча робота учня, яку він виконує, починаючи від ідеї і до втілення її в життя за допомогою консультацій учителя.
Такий навчальний процес базується на навчанні співпраці, а суть проектної технології в тому, що діти, враховуючи свої інтереси, разом з учителем виконують власний проект, розв'язуючи якусь практичну дослідницьку задачу. Включаючись таким чином у реальну дійсність, вони опановують нові знання.
Основні вимоги до методу проектів можна визначити трьома словами: Навіщо? Для чого (кого)? Як?
Перша вимога — наявність значущої для учня проблеми. Важливим моментом застосування методу проектів є те, що проблема не пропонується в готовому вигляді (як це спостерігається в проблемному методі), а з допомогою різних прийомів учні наштовхуються на самостійне формулювання проблеми. Формулювання проблеми — це і є відповідь на питання «навіщо?».
Друга вимога — це наявність практичного, теоретичного й пізнавального значення передбачу-вальних результатів, тобто учень повинен усвідомлювати, де і як можна застосувати здобуті знання, який продукт проекту буде його логічним завершенням.
Саме співвідношення проблеми й практичної реалізації її розв'язання і робить метод проектів досить привабливим для системи освіти.
Третя важлива характеристика методу проектів — це наявність самостійної (індивідуальної, парної, групової) роботи, використання дослідницьких методів.
Відомі різні класифікації проектів. Так, Є. С. Полат пропонує п'ять основних критеріїв, за якими розрізняють типи проектів.
1) За домінуючими в проекті методами:
• дослідницький (такі проекти повністю підпорядковані логіці дослідження і мають структуру що наближена чи повністю співпадає з істинно науковим дослідженням. Для реалізації застосовуються всі методи сучасної науки). Наприклад: лабораторний експеримент, соціальне опитування тощо;
- творчий (передбачається максимально довільний підхід до оформлення результатів). Наприклад: театральне інсценування з історії математики (тема «Винайдення шахів»), побудова макетів фігур (тема«Многокутники»);
- ігровий;
- інформаційний (збирання інформації про об'єкт дослідження з метою аналізу, узагальнення і представлення широкому колу слухачів. Такі проекти можуть інтегруватися в дослідницькі й ставати їхньою частиною);
- практично-орієнтовний (відрізняється чітко визначеним від самого початку результатом діяльності його учасників).Наприклад, створення посібника «Цікава математика».
2) За кількістю учасників:
- індивідуальний;
- парний;
- груповий.
3) За часом проведення:
- короткотривалий (1—3 уроки);
- середньотривалий (від одного тижня до одного місяця);
- довготривалий (кілька місяців, навіть років).
4) За характером контактів:
- внутрішні, або регіональні;
- міжнародні.
5) За предметно-змістовою ознакою:
- монопроекти (у межах одного предмета);
- міжпредметні.
Тематика проектів
На першому етапі проведення проектів важливе значення має вибір теми, що проходить по-різному: тему може запропонувати вчитель, враховуючи стан викладання предмета, здібностей та інтересів учнів. В інших випадках тематику можуть запропонувати самі учні. За мету можна поставити поглиблення знань учнів або диференціювання процесу навчання. Найчастіше теми проектів належать до конкретних практичних питань, що є актуальними в сучасному житті, тож для реалізації проекту необхідні знання учнів не лише з одного предмета, а з різних галузей. Саме в такий спосіб досягається природна інтеграція знань.
Зразки тем проектів
- Різноманітні підходи до розв'язування задач на рух.
- Історія натуральних чисел.
- Прийоми швидкого обчислення.
- Трикутники в житті й математиці.
- Застосування формул геометрії в реальному житті.
- Геометричні тіла довкола нас.
Етапи проведення проекту
Навчальні проекти здійснюються в декілька етапів, що відповідають головним етапам будь-якої трудової діяльності, їх реалізація носить циклічний характер. Можна виділити п'ять головних етапів реалізації навчального проекту:
- підготовчий;
- етап планування;
- дослідницький;
- презентативний (захист проектів);
- етап оцінно-рефлексивний оцінювання.
Зупинимось на кожному етапі.
Підготовчий. На цьому етапі важливий момент — визначення теми проекту. Пошук і аналіз проблеми. Вчитель та учні обговорюють спільну мету проекту, вчитель ознайомлює з правилами роботи в проекті, мотивує діяльність учнів, допомагає усвідомити мету. Обговорення методів дослідження.
Етап планування. Пошук оптимального способу досягнення мети проекту. Побудова алгоритму діяльності. Покрокове планування роботи. Визначення джерел інформації, способів презентації результатів, критеріїв оцінювання. Учні розподіляють поміж собою обов'язки, учитель лише висловлює ідеї та пропозиції.
Дослідницький. Практичне виконання запланованих кроків: учні здійснюють безпосередній збір інформації та аналізують її, виконують завдання щодо реалізації запланованих дій, при цьому вчитель спостерігає і консультує.
Презентативний. Оформлення кінцевого результату і проведення презентації, захист проектів. Це можна провести в будь-який спосіб: випуск газети, презентація чи публікація за допомоги ІКТ тощо. Під час захисту учні обговорюють результати з іншими дітьми, які не брали участі в їхньому проекті. Вчителеві відводиться роль звичайного слухача, він може ставити запитання, як і інші учні.
Оцінно-рефлексивний. Аналіз результатів, оцінювання якості проекту. Можна-проводити шляхом самооцінювання, колективного обговорення, анкетування, складання індивідуальних звітів тощо.
Роль учителя в проектній діяльності.
Із носія готових знань учитель перетворюється в організатора пізнавальної діяльності своїх учнів: допомагає учням у пошуку необхідних джерел інформації, сам є джерелом інформації, координує увесь процес, заохочує учнів, підтримує безперервний зворотний зв'язок для успішної роботи учнів над проектом.
Роль учня в проектній діяльності.
У ході виконання проектних завдань учень залучається до активного творчого процесу на підставі методики співпраці. Він занурюється в процес виконання творчого завдання, а заразом і в процес здобуття нових і закріплення набутих раніше знань із предмета, в рамках якого і здійснюється проект. Крім того, учень разом з учителем створює власний проект, розв'язуючи певне практичне, дослідницьке завдання. Включаючись таким чином у реальну діяльність, він опановує нові знання.
Приблизна схема структури навчального проекту.
- Автор навчального проекту(ПІБ, назва та адреса навчального закладу).
- Назва проекту (бажано яскрава і коротка).
- Основні питання: Ключові найбільш широкоформатні, екстрактні, не мають кінцевої відповіді, слугують для охоплення концептуальної структури групи навчальних тем, предмета, декількох предметів). Наприклад: Як математика допоможе мені зрозуміти навколишній світ?
- Тематичні (не мають конкретної відповіді, але зв'язані з конкретною темою, конкретизують ключові питання). Наприклад: Для чого мені необхідні квадратні корені?
- Змістовні (зв'язані зі змістом теми, мають спеціальні правильні, конкретні відповіді, які можна знайти в шкільному підручнику). Наприклад: Які властивості квадратних коренів ви знаєте?
- Анотація (короткий опис проекту).
- Навчальний предмет, у межах якого здійснюється проект.
- Навчальні дисципліни, зв'язані з проектом.
- Вхідні знання і навички учнів (ЗУН, які учні повинні матиперед початком проекту).
- Навчальні цілі й прогнозовані результати (перелік навчальних знань, умінь, якими будуть володіти учні по закінченню реалізації проекту).
- Державні стандарти й перелік програм.
- Вік учасників (клас).
- Термін, необхідний для реалізації проекту.
- Матеріали і ресурси (програмне забезпечення, публікації,ресурси Інтернет).
- Діяльність учнів, етапи проведення проекту.
Критерії оцінювання проекту:
- Характер оцінювання проектної діяльності залежить від типу, змісту, умов проведення проекту. Тому в кожному конкретному випадку це перш за все творчість учителя. Але під час розробки критеріїв оцінювання слід звернути увагу на такі аспекти:
- значимість і актуальність досліджуваних проблем, адекватність їх тематиці, що вивчається;
- коректність використаних методів дослідження і методів обробки здобутих результатів;
- активність кожного учасника проекту відповідно до його індивідуальних можливостей;
- колективний характер висновків;
- характер спілкування і взаємодопомоги учасників проекту;
- необхідний і достатній рівень проникнення в проблему, залучення знань з інших галузей;
- доказовість висновків, уміння аргументувати власні висновки;
- естетика оформлення результатів проекту;
- вміння давати відповіді на запитання опонентів.
Метод проектів як технологія, що спрямована на розвиток пізнавальної діяльності учнів, знаходить усе більше прихильників серед учителів і учнів. Це все природно, оскільки дає можливість:
- перевірити й закріпити на практиці теоретичні знання;
- забезпечити зв'язок між теорією та практикою;
- набути життєвого досвіду;
-
розвивати вміння аналізувати, систематизувати, узагальню
вати навчальний матеріал. - здійснювати пошукову, дослідницьку діяльність на підставі спільної праці;
- навчити користуватися додатковою літературою;
- виробляти вміння працювати самостійно над творчим завданням;
- підвищувати інтерес до математики;
- виховувати повагу, вміння працювати в колективі;
- формувати власну життєву позицію.
1.4 Правила організації інтерактивного навчання (тим педагогам, які вирішили працювати в інтерактивній технології).
Правило перше. До роботи повинні бути залученні всі учні, тобто всі вони повинні брати участь в процесі обговорення.
Правило друге. Треба потурбуватися про психологічну підготовку учасників. Справа в тому, що не всі учні, які прийшли на урок, психологічно готові до безпосереднього включення в ті чи інші форми роботи. Дає при себе знати скованість, традиційність поведінки. У зв'язку з цим корисні розминки, постійне заохочення учнів за активну участь в роботі, надання можливості для самореалізації учня. •
Правило третє. Тих учнів, які навчаються в інтерактивній технології, не повинно бути багато. Кількість учнів і якість навчання можуть виявитися в прямій залежності. В роботі повинно брати участь не більше, ніж ЗО учнів. Тільки при цій умові можлива продуктивна робота в малих групах. Адже важливо, щоб кожен був почутий, кожній групі надана можливість виступити з даної проблеми.
Правило четверте. Віднестись з увагою до підготовки класу чи іншого приміщення до роботи. Клас повинен бути підготовлений з таким розрахунком, щоб учасникам було легко пересаджуватися для роботи у великих та малих групах. Іншими словами, для учнів повинен бути створений фізичний комфорт.
Погано, якщо комусь на уроці прийдеться сидіти з "вивернутою" шиєю Тому столи краще поставити "ялинкою", щоб кожен учень сидів впівоберта до ведучого і мав можливість спілкуватися в малій групі. Добре, якщо завчасно будуть підготовлені матеріали, необхідні для творчої роботи.
Правило п 'яте. Віднестись з увагою до питань процедури і регламенту. Про це треба домовитися з самого початку і постаратися не порушувати його. Наприклад, корисно домовитися про те, що всі учасники будуть проявляти терпеливість до будь-якої точки зору, поважати право кожного на свободу слова, поважати його.
Правило шосте. Віднестись з увагою до поділу учасників семінару па групи. Спочатку його краще побудувати на основі добровільності. Потім доцільно скористатися принципом випадкового вибору.
- Наостанок слід зауважити, що інтерактивне навчання дозволяє розв'язувати одночасно кілька завдань. Головне - воно розвиває комунікативні уміння і навики, допомагає встановленню емоційних контактів між учнями, забезпечує розв'язання виховних завдань, оскільки привчає працювати в команді, прислухатися до думки своїх товаришів. І ще. Використання інтерактиву в процесі уроку, як показує практика знімає нервове навантаження школярів, дає можливість змінювати форми їх діяльності, переключати увагу на вузлові питання теми заняття.
- 1.4 Застосування інтерактивних методів навчання на уроках математики.
На своїх уроках я практикую сучасні технології. Саме на таких уроках учні вчаться бути демократичними, спілкуватися з іншими людьми, критично мислити, приймати продумані рішення.
Під час розв’язування більш складних задач, на своїх уроках я користуюсь такою інтерактивною технологією, як “Мозковий штурм”, що полягає в тому, що всі учасники штурму, після чітко поставленого проблемного запитання, висувають ідеї щодо розв’язування цієї проблеми. Один учень записує на дошці всі ідеї, що пропонуються, вибираються ті, що, на думку групи допоможуть розв’язати поставлену проблему.
Проводячи актуалізацію опорних знань учнів, на деяких уроках під час фронтального опитування я користуюсь ще однією інтерактивною формою роботи – “Мікрофон”, що надає можливість по черзі кожному висловитись швидко, відповідаючи на запитання.
Наприклад, визначивши тему, з якої учні будуть висловлюватися в колі ідей, або, використовуючи уявний мікрофон, формулюю незакінчене речення і пропоную учням, висловлюючись, закінчувати його. Кожний наступний учасник обговорення повинен починати свій виступ із запропонованої формули. Учні працюють з відкритими реченнями, наприклад: “Ця інформація дозволяє нам зробити висновок, що ...” або “Це рішення було прийнято тому, що ...”, “На сьогоднішньому уроці для мене найбільш важливим відкриттям було ...”.
Наприклад, під час вивчення теми “Чотирикутники” у 8 класі розв’язуючи задачу :
У паралелограмі ABCD точка E – середина сторони ВС, а F – середина сторони AD. Доведіть, що чотирикутник AECF паралелограм.
До цієї задачі пропоную даний рисунок.
B Е С



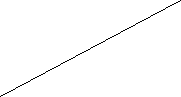
A F D
Спочатку учні виконують рисунок в зошиті і самостійно деякий час обмірковують розв’язування задачі. Колективне обговорення ходу розв’язання і одночасне повторення теоретичного матеріалу можна провести, використавши в поєднанні прийом “Мікрофона” і “Незакінченого речення”.
Пропоную ряд запитань і завдань, заготовлених на звороті дошки ще до початку уроку. Учні, передаючи уявний мікрофон один одному, висловлюються по черзі, не обов’язково в порядку поставлених запитань.
Запитання і завдання для обговорення:
- Про паралелограм ми знаємо, що ...
- Про чотирикутник можна сказати, що він є паралелограмом, якщо ...
- Інформація, що Е – середина сторони ВС, дозволяє нам зробити висновок, що ...
- Інформація, що F – середина сторони AD, дозволяє нам зробити висновок, що ...
- Чи є серед утворених трикутників рівні і якщо так, то обґрунтуйте це.
- Інформація про рівність трикутників AFE і CEF дозволяє нам зробити висновок, що ...(і чому?)
- Інформація, що ABCD паралелограм дозволяє нам зробити висновок, що ...
- Розгляньте чотирикутник AECF.
- Яку ознаку паралелограма можна використати для чотирикутника AECF?
- Зробіть висновок, закінчивши речення : “Я вважаю, що AECF паралелограм тому, що ...”
Під час узагальнення та повторення вивченого використовую іншу форму інтерактивного навчання «Навчаючи - учуся». Роздаю картки з питаннями теоретичного характеру, по одній на кожного учня. Протягом 1 хв. учні читають питання на картці та зосереджуються на відповіді. Учні ходять по класу і знайомлять зі своєю інформацією інших однокласників. Учням дозволяю одночасно говорити тільки з однією особою. Завдання полягає в тому, щоб поділитися своєю думкою і самому отримати інформацію від іншого учня. Після того, як учні завершать дану вправу, пропоную їм розповісти, відтворити отриману інформацію. Аналізую та узагальнюю отримані знання учнів. На проведення таких вправ на уроці відводжу 10 хв.
Використовуючи інтерактивні технології навчання на уроках математики впроваджую метод “Акваріум”. Об’єдную учнів у групи по 4 – 6 осіб і пропоную їм ознайомитися із завданням.
Одна з груп сідає в центр класу (або на початку середнього ряду в класі, де стоять парти). Це необхідно для того, щоб відокремити діючу групу від слухачів певною відстанню.
Ця група отримує завдання для проведення групової дискусії, сформульоване приблизно так:
- прочитайте завдання вголос;
- обговоріть його в групі;
- за 3 –5 хвилин дійдіть спільного рішення або підсумуйте дискусію.
Поки діюча група займає місце в центрі, знайомлю решту класу з завданням і нагадую правила дискусії у малих групах. Групі пропоную вголос протягом 3 –5 хвилин обговорити можливі варіанти розв’язання проблемної ситуації. Учні, що знаходяться у зовнішньому колі, слухають, не втручаючись у хід обговорення, лише піднімають сигнальні картки в разі виявлення помилки.
По закінченні відведеного для дискусії часу група повертається на своє місце, а вчитель ставить до класу такі запитання:
- Чи погоджуєтесь ви з думкою групи?
- Чи була ця думка достатньо аргументованою, доведеною?
- Який з аргументів ви вважаєте найбільш переконливим?
На таку бесіду відводжу не більше 2-3 хвилини. Після цього місце в “Акваріумі” займає інша група і обговорює наступну ситуацію.
Наприкінці обговорюю з учнями хід групової роботи, коментую ступінь оволодіння навичками дискусії у малих групах і звертаю увагу на необхідність та напрям подальшого вдосконалення таких навичок. У межах “Акваріума” можна підбити підсумки уроку або за браком часу обмежитись обговоренням роботи кожної групи.
Під час проведення роботи за методом “Акваріума” учням необхідно багато логічних кроків робити усно. А це позитивно впливає на творче осмислення теоретичних надбань і сприяє інтелектуальному розвитку учнів. Крім того, учні цим збагачують свою уяву, вчаться прогнозувати результат, відпрацьовують культуру мови і послідовність думки, збагачуються духовно взаємним спілкуванням.
Використовую ще один відомий спосіб роботи учнів у групах – “Ажурна пилка”, який дозволяє вивчити значну кількість інформації за короткий час, а також заохочує учнів допомагати один одному вчитися навчаючи.
Також проводжу підсумкові уроки з теми у вигляді уроку-гри, навожу конспект уроку з геометрії „Перпендикулярність прямих і площин ” у 10 класі (бізнес-гра), конспект підсумкового уроку з теми „Десяткові дроби ” „Розв’язування вправ ” (метод проектів) 5 клас, конспект уроку «Подорож геометричною країною» 5 клас, конспект уроку з теми «Дії з натуральними числами» (урок-подорож) 5клас.
- Додатки.
2.1 Конспект уроку „Перпендикулярність прямих і площин ” (бізнес-гра) 10 М клас
ТЕМА: ”Перпендикулярність прямих і площин”
Бізнес-гра.
Мета: перевірити і систематизувати знання учнів з теми „Перпендикулярність прямих і площин”; розвивати логічне мислення, увагу, самостійність; виховувати інтерес до предмета.
Обладнання: ватмани, маркери, листочки з завданнями для усного та письмового розв’язування.
ХІД УРОКУ
I. Організаційний момент.
На дошці записано тему уроку, яку оголошує вчитель та пояснює правила бізнес-гри.
Учні класу об'єднуються у команди, кожна з яких — це правління певного банку; капітан команди — це президент банку, члени команди — правління банку. Назва кожного банку представлена табличкою на столі: банк «Аваль», банк «Омега», «Інтербанк», «Мегабанк»,
Президент має право вирішального голосу у випадку, коли думки членів правління банку не збігаються.
- Придбання початкового капіталу.
Командам по черзі пропонують запитання та задачі. Якщо відповідь правильна, то бали додаються, якщо ні — бали віднімаються і придбати це запитання або задачу може інший банк, але вже за ціною на 1 бал меншою.
1. Запитання для усного опитування.(по 3 запитання для кожної команди)
(Кожне запитання оцінюється у 5 балів.)
- Означення перпендикулярності прямої та площини.
- Ознака перпендикулярності прямої та площини.
- Теорема про три перпендикуляри.
- Означення перпендикулярності площин.
- Ознака перпендикулярності площин.
- Відстань від точки до площини.
- Відстань від прямої до площини.
- Відстань між паралельними площинами.
- Перпендикуляр до площини.
- Відстань між мимобіжними прямими.
- Похила і проекція.
- Властивості похилих.
Вчитель заповнює таблицю отриманих балів.
2. Задачі для усного розв'язування.
(Кожна задача оцінюється у 10 балів.)
1. Відомо, що SO I (ABC), SA = SB ∆ABC — прямокутний.
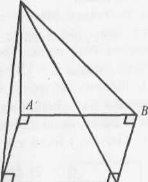
Пояснити розміщення точки О.
2. Відомо, щоABCD— прямокутник, КА ┴(ABC). Де на малюнку відрізок, довжину якого можна вважати відстанню від точки К до С В?
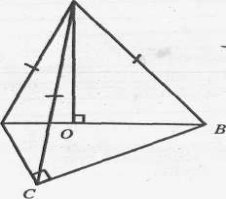
3. Відомо, що SO┴(ABC), SP = SN = SK. Пояснити розміщення точки О.
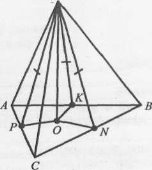
4. Відомо, що KB ┴ (ABC), ∆ABC - прямокутний. Пояснити, чому КС є відстанню від точки К до АС.
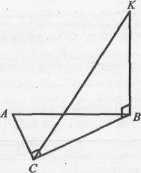
5.Відомо, що KC┴(ABC), ∆ABC – рівнобедрений. Пояснити, чому КО є відстанню від точки К до АВ
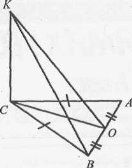
III. Аукціон задач.
Учитель виставляє задачу, як лот, на торги. Представник банку, що швидше її розв'яже, пояснює розв'язання біля дошки. Задачі 1,3 оцінюються у 5 балів, задача 2 — у 10 балів.
Задача 1. Відстань від точки М до всіх вершин квадрата дорівнює 5 см. Знайти відстань від точки М до площини квадрата, якщо діагональ квадрата 6 см.
Задача 2.Відрізок ВМ перпендикулярний до площини прямокутника ABCD. Довести, що пряма CD перпендикулярна до площини МВС.
Під час оформлення і підготовки розв’язку задачі одним учнем на дошці решту учнів виконують логічну задачу.
Задача 3. (Логічна.) Який квадрат зайвий?
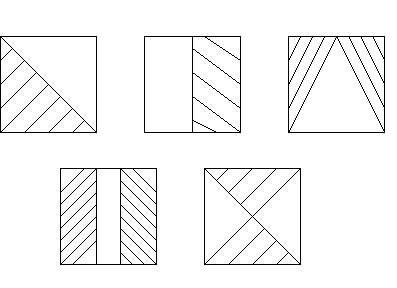
IV. Розв'язування задач.
Кожний учень команди отримує задачу та листок на якому будує малюнок та розв’язує задачу. Задачі підбираються відповідно до рівня навченості учнів.
-
Побудуйте зображення куба АВСDА1В1СІD1 і запишіть грані куба,
які перпендикулярні до площини А1АС . (З бали)
- Дано прямокутний трикутник АВС з гіпотенузою АВ. До площини трикутника АВС проведено перпендикуляр ВМ. Знайдіть величину кута МСА. (З бали).
- До площини квадрата АВСD проведено перпендикуляр SВ. Знайдіть величину кута SАD. (З бали).
- Точка М знаходиться на однаковій відстані від всіх сторін правильного трикутника зі стороною 12 см і віддалена від площини трикутникa на 2 см. Знайдіть відстань від точки М до сторін трикутника. (З бали)
- Ребро куба дорівнює а. Знайдіть відстань між діагоналлю куба і діагоналлю грані куба, яка мимобіжна з діагоналлю куба. (З бали )
- Кожне ребро трикутної піраміди дорівнює а. Знайдіть відстань між двома ребрами, які є мимобіжними (3 бали).
Відповідь.1. ABCD і А1В1СІD1 , 2.< МСА=90, 3. <SАD=90 , 4. 4 см , 5. а/√6, 6. а/√2.
Вчитель роздає аналогічні задачі кожній команді учні їх розв’язують та здають на перевірку. Вчитель проводить обговорення розв’язування цих задач і залучає до цього учнів.
Кожен учень отримує бали за розв’язану задачу і ці бали додаються до балів команди.
V. Підсумок уроку.
За кількістю набраних балів визначають банк-переможець. (аналізується кількість балів у таблиці)
Роботу всіх учасників гри вчитель оцінює за їх участю у розв'язуванні завдань.
VI. Домашнє завдання.
Підготуватись до контрольної роботи. Повторити §1, 3.
№7, 15,32(с.34-39)
- Конспект підсумкового уроку з теми „ Десяткові дроби” (метод проектів) 5 клас.
Тема. Розв'язування вправ.
У II семестрі учні починають вивчати дроби та дії над ними. Вони вивчають спочатку тему «Звичайні дроби», а потім «Десяткові дроби». Під час узагальнення вивченої теми слід поєднувати її з попередніми, щоб учні розуміли математику як єдине ціле. Це урок узагальнення і систематизації знань.
Використовується нестандартна форма проведення — захист проектів. На всіх етапах уроку використовуються активні форми навчання. Під час актуалізації опорних знань: «Мікрофон» (кожна група по черзі презентує свій проект, повторюючи правила, означення, склавши опорну схему), «Прес», «Дивись не помились». Під час закріплення вмінь та навичок — робота в малих групах (по 4-5 учнів), вправи на кмітливість.
Засобами наочності є картки з диференційованими завданнями, підручник, опорні схеми, складені самими учнями.
Спочатку учні захищають власні проекти. Таким чином, вивчений матеріал буде узагальнений і систематизований. Для цього учнів слід об'єднати в 5 груп: 1-ша група — «Звичайні дроби», 2-га група - «Дії зі звичайними дробами», 3-тя група — «Десяткові дроби», 4-та група — «Дії з десятковими дробами», 5-та група — «Експерти». У кожній з перших чотирьох груп є теоретики, дослідники та практики. Клас працює разом з кожною групою. Таким чином, усі учні класу закріплять набуті вміння та навички за всіма видами дробів.
Мета уроку: сприяти активізації пізнавальної діяльності учнів, здійснювати організовану пошукову, дослідницьку діяльність на основі спільної праці учнів; зацікавити учнів проектом, створити творчі групи, визначити коло обов'язків, вчити вмінню самостійно працювати над творчими завданнями; залучати учнів до чарівного світу дробів; повторити види дробів, правила порівняння, додавання, віднімання дробів як звичайних, так і десяткових, округлення звичайних дробів; закріпити вміння та навички використання правил під час розв'язування прикладів. Поєднати різні види дробів в одному прикладі; розвивати логічне та нестандартне мислення, творчі здібності, увагу, кмітливість, самостійність. Виховувати почуття доброти, співчуття, бажання прийти на допомогу, вміння працювати групами, цікавість до предмета.
Тип уроку: узагальнення та систематизація знань.
Комплексне використання методів: проблемне навчання, пошуковий, особистісно-орієнтований, інтерактивний (групова робота), метод проектів.
Література: Мерзляк А. Г, Полонський В. Б., Якір М. С.Підручник «Математика. 5 клас»; «Збірник задач і завдань для тематичного оцінювання».
Обладнання: підручник, картки, опорні схеми.
Структура уроку
- Організаційна хвилинка. Визначення теми та мети уроку.
- Мотивація навчальної діяльності.
- Актуалізація опорних знань. Захист проектів (повторення теоретичного матеріалу, використовуються активні методи: «Дивись не помились»,«Мікрофон», «Прес»).
- Робота в малих групах.
- Робота з підручником, розв'язування спільних вправ.
- Підбиття підсумку уроку (у формі бесіди).
ХІД УРОКУ
Числа не керують світом, але вони показують, як ним керувати.
Г. Лейбніц
Найкращий спосіб вивчити що-небудь — це відкрити самому.
Д. Пойа
І. Повідомлення теми та мети уроку
Шановні учні! Ми закінчили з вами вивчати теоретичний матеріал з теми «Десяткові дроби». Сьогодні наша мета — узагальнити й систематизувати набуті знання з теми, пригадати, які ще дроби ми вивч в попередній темі. Повторити правила, означення, закріпити набуті вміння та навички.
II. Мотивація навчальної діяльності
Ви вже знаєте, що з давніх-давен доводилось не лише лічити предмети, а й вимірювати довжину, обчислювати площі, вести розрахунки за куплені й продані товари. Не завжди результат вимірювань чи вартість товару можна було виразити натуральним числом. Так з'явились дроби. У старших класах ви будете працювати одночасно з усіма видами дробів, тому сьогоднішній урок дуже важливий.
Робота, проведена учнями та вчителем у ході підготовки проектів:
Розподіл обов'язків
Проект колективний. Утворюються п'ять груп учнів. Міні-групи добирають назву, визначають напрямки роботи, готують необхідні матеріали, аналізують їх, упорядковують, консультуються з керівниками груп, подають свою роботу у вигляді схем. Для захисту проекту визначаються теоретики, дослідники, практики та група експертів (учні, які навчаються на високому рівні). Ця діяльність відбувається на попередніх уроках.
План роботи
Урок 1 (під час узагальнення вивченого матеріалу з теми «Звичайні дроби»)
1. Обґрунтувати назву проекту, реальність її розв'язання: вікові та психологічні особливості школярів різних груп, час для підготовки.
- Розподіл обов'язків, вибір керівників груп.
- Збирання матеріалу.
Урок 2 (під час вивчення десяткових дробів)
- Ознайомлення із зібраним матеріалом групою «Теоретики», його аналіз, упорядкування.
- Консультації з керівниками груп, координаторами проекту.
Урок 3 (під час вивчення десяткових дробів)
- Упорядкування та аналіз матеріалу, підібраного групою «Дослідники».
- Створення проблемної ситуації. Пошук її розв'язання.
- Написання творчих робіт.
Урок 4 (під час вивчення десяткових дробів)
- Підбір та аналіз матеріалу групою «Практики».
- Виконання відповідних обчислень.
- Виготовлення наочності.
Засідання 1 (під час вивчення десяткових дробів)
- Упорядкування, оформлення проекту.
- Складання сценарію захисту проекту.
- Корекція помилок.
Засідання 2 (під час узагальнення теми «Десяткові дроби»)
- Презентація і захист проекту.
- Оцінка виконаної роботи.
- Практичний результат реалізації проекту.
-
Оформлення стіннівки.
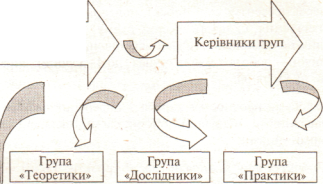
![]()
![]() Координатор проекту
Координатор проекту
Схема роботи над творчим проектом
III. Актуалізація опорних знань
Група 1. Презентація проекту «Звичайні дроби»
«Теоретики»
Запис, в якому використовують два натуральні числа і риску дробу, називають звичайним дробом.
Види звичайного дробу
/ \
правильний неправильний
чисельник < знаменника чисельник >, = знаменнику
![]() мішане число = ціла частина + дробова частина
мішане число = ціла частина + дробова частина
правильний дріб
«Дослідники»
Порівняння дробів
/ \
З однаковими 3 однаковими
знаменниками чисельниками
![]()
![]() Неправильний дріб перетворити у мішане число
Неправильний дріб перетворити у мішане число
Чисельник поділити на знаменник
![]()
![]() Мішане число перетворити в неправильний дріб
Мішане число перетворити в неправильний дріб
Цілу частину помножити на знаменник і додати чисельник
«Практики»
№ 1. Наведіть приклади правильних і неправильних дробів.
№ 2. Порівняйте:
№ 3. Перетворіть неправильний дріб у мішане число:
№ 4. Перетворіть мішане число в неправильний дріб:
Група 2. Презентація проекту «Дії зі звичайними дробами»
«Теоретики»
![]()
 Чисельники однакові
Чисельники однакові
Додавання Віднімання
чисельник + чисельник, чисельник - чисельник
а знаменник залишити зменшуваного від'ємника,
той самий а знаменник залишити
той самий
«Дослідники»
![]() Мішані числа
Мішані числа
![]()
Додавання Віднімання
Окремо додати їх цілі Від цілої і дробової частини та
Та дробові частини зменшуваного відняти цілу й дробову частину від’ємника.
«Практики»
Виконайте дії:
IV. Узагальнення і систематизація знань
Група 3. Презентація проекту «Десяткові дроби, порівняння, округлення»
«Теоретики»
Десятковий дріб
![]()
Це дріб, у якого знаменник є степенем десяти, тобто числами 10, 100, 1000 і т. д.
Кома - відокремлює цілу та дробову частини.
![]()
![]()
![]()
![]()
![]()

![]() Наприклад: 22,45678
Наприклад: 22,45678
Десятки одиниці десяті соті тисячні
десятитисячні стотисячні
«Дослідники»
![]()
![]() Порівняння
Порівняння
![]() Різні цілі частини Рівні цілі частини
Різні цілі частини Рівні цілі частини
![]() Більше той, у якого Порівнюють порозрядно
Більше той, у якого Порівнюють порозрядно
більша ціла частина дробові частини
Округлення
Якщо перша з цифр, яку відкидають, дорівнює
![]()
![]()
0,1,2,3,4 5,6,7,8,9
то остання з цифр, яка залишається
![]()
![]()
не змінюється збільшується на одиницю
«Практики»
1. Порівняйте:
а) 20, 297 і 20, 3; б) 0,724 і 0,7238.
2* Які цифри можна поставити замість зірочки, щоб утворилася правильна нерівність (у правій і лівій частинах * позначено одну й ту саму цифру)?
а)0,*2>0,6*; б) 0,*5 <0,5*. 3. Округліть:
а) до десятих: 7,236; 0,85834;
б) до тисячних: 16,9264; 0,4566.
4. Які цифри можна підставити замість зірочки, щоб округлення було виконано правильно? 5,47*4 ~ 5,47.
Група 4. Презентація проекту «Додавання та віднімання десяткових дробів»
«Теоретики»
Властивості додавання
Переставна Сполучна
a+b=b + a (a+b)+c = a+(b + c)
«Дослідники»
Правило додавання та віднімання:
- зрівняти кількість цифр після коми,
-
приписавши праворуч необхідну кількість нулів
до одного з чисел, записати «у стовпчик» розряд
під розрядом; - виконати відлові дну дію.
«Практики»
- Виконайте дії: 34,7-(6,76+0,987).
- Запишіть у метрах і обчисліть: 18,2 м — 67 см.
- Задача.
Ламана складається з трьох ланок. Довжина першої ланки 8,2 см, що на 3,7 см більше за довжину другої ланки і на 5, 3 см менше від довжини третьої. Чому дорівнює довжина ламаної?
V. Закріплення вмінь та навичок
Група 5.
«Експерти».
Оцінює учнів кожної групи, робить підсумок, вказує на недоліки й пропонує розв'язати завдання.
- № 871*, с. 211 підручника.
- Розв'яжіть рівняння (х -50,6) +2,15 = 42,9.
3) Обчисліть:
4) Знайомство з історичною довідкою (учні збирають самі).
Сучасне позначення дробів бере свій початок у Стародавній Індії. Його стали використовувати й араби, а від них у XII—XIV ст. було запозичено європейцями. Спочатку в запису не використовувалася дробова риска. Наприклад, дроби -, 2 - записували так: ; 2 .
Риску дробу стали постійно застосовувати лише близько 300 років тому.
Першим європейським ученим, який став використовувати і розповсюджувати у 1200 році сучасний запис дробів, був італійський купець і мандрівник Леонардо Пізанський. Він увів слово «дріб». Назву чисельник і знаменник увів у XIII ст. Максим Пеа-унд - грецький монах, учений-математик.
У науці й промисловості частіше використовуються десяткові дроби. Це пов'язано з тим, що правила обчислення з десятковими дробами дуже прості й схожі на правила виконання дій з натуральними числами.
В Європі вчення про десяткові дроби першим виклав голландський математик і інженер Симон Стевін, праця під назвою «Десята» (1585 p.). Записував він десяткові дроби інакше. Наприклад, число 28,375 записував так: 28Ф Зф 7ffl 5e, де цифри в кружечках показували місце десяткових дробів.
Кому як знак дробовості увів відомий математик, фізик, астроном І. Кеплер.
Цікаве і влучне «арифметичне» порівняння робив Л. М. Толстой. Він говорив, що людина подібна до дробу, знаменник якого є те, що людина про себе думає, а чисельником — те, що людина являє собою. Чим більшої думки людина про себе, тим більший знаменник, а значить, менший дріб.
VI. Підсумок уроку
1. Прочитайте і назвіть, що це
2. Які дії з дробами ми виконували сьогодні на уроці?
VII. Домашнє завдання (диференційоване)
I рівень. № 747, 748 (1, 2), 795, 889.
IIрівень. № 751 (6, 7), 798, 908.
2.3 Урок «Подорож геометричною країною» 5 клас.
Тема: « Подорож геометричною країною»
Мета: закріпити знання учнів про геометричні фігури і величини; формувати вміння зображати їх графічно, застосовувати властивості геометричних фігур до розв'язування задач практичного змісту; розвивати інтерес до математики, збудити прагнення більше знати, розуміти; розвивати творчі й інтелектуальні здібності учнів; виховувати почуття колективізму, взаємодопомоги, відповідальності за доручену справу.
ХІД УРОКУ
І. Організаційний момент, мотивація навчальної діяльності
Французький математик, фізик і філософ Блез Паскаль вважав: «Предмет математики такий серйозний, що не варто нехтувати нагодою робити його трохи цікавішим». Сьогодні відбудеться не-I звичайний урок. Це урок-мандрівка до Країни геометричних | Фігур.
У мандрівці беруть участь учні 5-го класу, об'єднані в три команди (за рядами). Команди мають назви «Пряма», «Трикутник», «Кут».
Під час мандрівки всі команди вівідають кілька станцій та виконають завдання, які оцінюватимуться фігурками трикутників, чотирикутників, кружечків (відповідно для кожної команди). За їх кількістю в кінці уроку буде встановлено, яка команда першою прибуде до Країни геометричних фігур.
Люблю мандрівки, люблю походи, і
Чи світить сонце, чи знов негода
Ми вже в дорозі, вітер в обличчя, Геометричний край до себе кличе!
II. Мандрівка до країни геометричних фігур
Станція «Теоретична»
- Троє учнів (по одному від кожної команди) на дошці зображають фігуру, що є назвою його команди, із відповідними позначеннями основних елементів фігури і наступним обґрунтуванням. Робота супроводжується формулюванням відповідних означень, властивостей. Під час оцінювання враховуватиметься правильність рисунка, чіткість обґрунтування. Накресліть трикутник ABC.
- Укажіть сторони трикутника смк.
- Накресліть прямокутний трикутник/405, (Z0 = 90°).
- Накресліть трикутник MDK тупий).
З іншими учнями класу проводиться фронтальна робота.
Кожній команді пропонуються 10 завдань. Якщо команда відповіла на всі запитання, то отримує фігурку, що відповідає назві своєї команди.
Завдання команді «Пряма»
- Накресліть відрізок АВ.
- Накресліть промінь СК.
- Накресліть пряму DM.
- Накресліть ламану ABCDK.
- AM = 48дм, АВ = 30дм. Знайдіть довжину відрізка ВМ.
- Знайдіть довжину прямої AM.
-
 Запишіть відрізки, зображені на рисунку. А В С Д
Запишіть відрізки, зображені на рисунку. А В С Д
- Позначте точки М і К, які на лежать прямій а; А і С, які не належать прямій а.
- Скільки прямих можна провести через одну точку?
10. Скільки прямих можна провести через дві точки?
Завдання команді «Трикутник»
- Накресліть трикутник ABC.
- Укажіть сторони трикутника СКМ.
- Накресліть прямокутний трикутник АОВ, ( ‹0 = 90°).
- Накресліть трикутник MDK (‹Д-тупий).
- Накресліть гострокутний трикутник САВ.
- Які бувають трикутники залежно від мір кутів?
- Які бувають трикутники залежно від довжин сторін?
- Як знайти периметр трикутника?
-
Чому дорівнює сума всіх кутів довільного трикутника?
- Визначте вид трикутника, зображеного на рисунку.
Завдання команді «Кут»
- Як позначається кут?
- Запишіть символічно:
а) кут АОВ;
б)кут О.
3. Запишіть вершини, сторони кутів, зображених на рисунку.

4,Укажіть вид кута:
a) ‹А=76°
б) ‹ В=94°
в) ‹ М=123°
г) ‹C = 90°.
5. Накресліть:
а) ‹COD — гострий;
б) ‹РКМ — розгорнутий.
6. Накресліть:
а) ‹ABM — тупий;
б) ‹CMK — прямий.
- Побудуйте ‹M = 58°.
- Побудуйте ‹А = 90°.
- Побудуйте ‹C = 146°.
- Побудуйте ‹Z = 74°.
- Побудуйте ‹В= 180°.
Станція «Художня»
Стануть фігури танцювати, зможуть шедеври малювати! Представники від кожної команди виконують рисунок, який складається лише з геометричних фігур, на одну з тем: «Дім, сад, город», «На відпочинку», «Птахи і звірі» тощо. На виконання завдання відводиться 5-7 хв. Решта учнів класу виконують рисунки у зошитах.
Під час оцінювання рисунка враховується якість виконання та кількість використаних - геометричних фігур.
Станція «Практична»
Учні, застосовуючи властивості геометричних фігур, формули площ і периметрів многокутників, розв'язують задачі практичного змісту.
Задача 1 (усно): Скільки метрів огорожі необхідно для того, щоб загородити земельну ділянку, що має форму квадрата зі стороною 15м?
Задача 2 (усно). Яку площу має дачна ділянка прямокутної форми, якщо ширина цієї ділянки 20 м, а довжина в три рази більша?
Задача 3. Прямокутне поле завдовжки 1 км 600 м і завширшки 625 м засіяли житом. На 1 га висівали по 120 кг зерна. Скільки жита висіяли на цьому полі?
Розв'язання
- 1 км 600м = 1600м; 1 га = 10 000 м2.
- 1600 -625 =1000 000 (м2) == 100 (га) — площа поля.
- 120-100=12000(кг) = 12(т)- висіяли жита.
Відповідь. 12 т
Станція «Веселі рибалки»
На озеро математичне,
На озеро логічне,
Вирушаємо ми!
Питання е серйозні,
А є і жартівливі.
Тож будьте ви уважні,
і будьте ви кмітливі!
Представники від кожної команди «ловлять» вудочкою, до якої прикріплено магніт, «рибку» із запитаннями, на які дають відповіді.
Запитання на «рибках»
- Мікроскоп збільшує розміри дуже маленького прямокутника. Але в прямокутнику є те, чого мікроскоп не може збільшити. Що це?
-
Кришка стола має чотири кути. Один із них відпиляли. Скільки
стало кутів? - Колесо має 10 спиць. Скільки проміжків між спицями?
- Як із 13 рівних квадратів скласти два квадрати?
- На розграфленій квадратній дошці розміром 5x5 Катя замалювала всі квадратики, які лежать на діагоналях. Скільки квадратиків замалювала Катя?
Станція «Логічна»
Учитель демонструє учням малюнки або фігури і пропонує, користуючись ними, виконати певні завдання.
Завдання 1. Вставте пропущене число

З ? 10
(6 — кількість кутів, зображених на рисунку)
Завдання 2. Як із прямокутного клаптя тканини вирізати квадратну хустинку, користуючись лише ножицями?
Завдання 3. Як із 13 сірників, кожен з яких має довжину 4 см 5 мм, скласти метр? (МЕТР)
Завдання 4. Як треба розрізати квадрат, щоб із нього можна було б скласти трикутник?
 Відповідь.
Відповідь. 
Завдання 5. На торті є 7 троянд. Як трьома прямими розрізами розділити торт на 7 частин так, щоб у кожній було по одній троянді?
Відповідь
III. Підсумок уроку
Учитель Найдавніша на планеті, Між наук цариця, — Математика, ти наша Вірна помічниця. Чи будинок зводиш, друже, Чи пливеш морями — Скрізь вона тобі послужить, Всюди вона з нами.
Учитель. Ви гарно впоралися із завданнями, подолали всі випробування. Тепер ми визначимо, яка команда першою прибула до Країни геометричних фігур. (Визначаються команда-переможниця. Та найактивніші учасники подорожі.)
IV. Завдання додому
Скласти цікаві ігри із застосуванням геометричних фігур.
2.4 Конспект підсумкового уроку з теми «Дії з натуральними числами»
Тема. Дії з натуральними числами (урок-подорож)
Мета: узагальнення та систематизація знань; формування обчислювальних навичок; вдосконалення вміння розв'язувати рівняння із застосуванням правил залежності між компонентами дій; відпрацювання навичок множення та ділення на розрядну одиницю.
Тип уроку. Урок повторення та систематизації знань.
Обладнання: картки з назвами вулиць, правилами, круговими прикладами, рівняннями, цікавими задачами.
ХІД УРОКУ
І. Вступне слово вчителя.
Вивчаючи математику, ми намагаємося відповісти на запитання, для чого людям потрібні числа та математичні вирази, уміння виконувати над ними різні дії та перетворення. Математики прагнуть замінити довгі пояснення про розглянуті явища короткими формулами, що містять усі необхідні дані. Ви повинні навчитися терпляче розшифровувати математичні вирази, щоб зрозуміти їх зміст. Тоді відповідь на запитання, які бувають числа і для чого необхідно добре знати правила дій над ними, з'явиться сама собою.
Сьогодні я запрошую вас у подорож по місту Натуральних чисел.
II. «Вулиця Правил».
Увійшовши у місто, ми відразу потрапляємо на вулицю Правил. Усі жителі тут дуже правильні, і щоб познайомитися з господарем кожного будинку, необхідно згадати відповідне правило.
( У планшет з картою вулиці впереміш вміщено пронумеровані картки із завданнями. Учні по черзі називають номер будинку, що відповідає номеру картки, та виконують відповідне завдання. Кількість балів, що виставляються, дорівнює кількості фішок, які одержує учень, і відповідає складності завдання.)
Завдання на картках
- Назвіть компоненти додавання.
- Назвіть компоненти віднімання.
- Назвіть компоненти множення.
- Назвіть компоненти ділення.
- Сформулюйте переставний закон множення.
- Сформулюйте переставний закон додавання.
- Сформулюйте сполучний закон множення.
- Сформулюйте сполучний закон додавання.
- Сформулюйте розподільний закон множення.
- Як знайти невідомий доданок?
- Як знайти невідоме зменшуване?
- Як знайти невідомий від'ємник?
- Як знайти невідомий множник?
- Як знайти невідоме ділене?
- Як знайти невідомий дільник?
Завдання 1—4 оцінюються одним балом; 5, 6, 10—15 — двома балами; 7—9 — трьома балами.
III. «Площа Кругових прикладів».
Після вулиці Правил ми потрапляємо на площу Кругових прикладів. Жителі цієї площі все роблять по колу. Тому, щоб дізнатися про них більше, необхідно розв'язати «кругові приклади».
(Учням роздаються картки з двома варіантами «кругових прикладів». Двоє учнів по одному від кожного варіанта розв'язують приклади на дошці, інші виконують завдання в зошитах. Той учень, хто розв'язав приклади швидше, ніж на дошці, одержує додаткові фішки. Кожен приклад оцінюється двома балами.)
Перший варіант
- 1249 + 34872 = а;
- а – 35730 = в;
- в :23 = с;
- с * 534 = д;
- д + 12547 = е;
- е – 21613 = ф.
Другий варіант
- 538 * 47 = а;
- а – 25212 = в;
- в * 435 = с;
- с+3847 = е;
- е – 35473 = д;
- д : 47 = ф.
IV. «Провулок Усної лічби».
Жителі провулка Усної лічби бажають передати нам якесь повідомлення. Для того щоб його побачити, потрібно виконати кожен із запропонованих прикладів.
(Учні складають математичне лото. На картках записано приклади для усної лічби на множення та ділення на розрядну одиницю. На зворотному боці карток зображено частини малюнка, який утвориться після правильного виконання завдань. Кожен приклад оцінюється одним балом.)
Завдання на картках
- 150: 10;
- 73 800 000 : 1000;
- 6530 • 10;
-
48 900 : 100;
5.31-100;
- 906 • 10 000;
- 89 000 : 100;
- 390 • 100;
- 384 • 1000;
- 35 000 : 1000;
- 780 000 : 10 000;
- 56 • 10;
- 357 000 : 1000;
- 7840 • 100;
- 356 000 : 100.
V. «Проспект Рівнянь».
Жителі цього проспекту — великі вигадники — зашифрували його назву. Щоб її дізнатися, потрібно розв'язати рівняння.
(Учням роздаються картки з рівняннями. Один учень розв'язує рівняння біля дошки, інші виконують завдання в зошитах. Ті, хто виконає завдання швидше, ніж на дошці, одержують додаткові бали. На аркуші з назвою проспекту є картки з відповідями, на зворотному боці яких записано літери, що входять до назви проспекту. Кожне рівняння оцінюється двома балами.)
Завдання на картках Розв'язати рівняння:
1.21-(18+х) = 714;
- (х+14):9 = 13;
- (46-х)-19 = 418;
- 966: (х- 17) = 23;
-
1728: (56-х) = 36;
6.17- (х+ 16) = 576.
VI. « Бульвар Загадок».
Ті, хто мешкають на цьому бульварі, дуже загадкові. Тому всім, хто сюди потрапляє, вони загадують свої задачі-загадки.
(На дошці вивішуються таблиці із задачами. За кожну правильно розв'язану задачу учні отримують три бали.)
Задачі-загадки
1. Тарас і Єгор за 3 год надрукували 21 сторінку. Єгор за 1 год друкує чотири сторінки. Скільки сторінок друкує Тарас за 1 год?
(Три сторінки)
- Поставте замість зірочок знаки дій і дужки так, щоб рівність була правильною:
1*2*3*4*5 = 100.
(1 • (2 + 3) • 4 • 5 = 100)
3. Які малюнки повинні бути замість знаків питання?
(Трикутник, шість променів)
4.Яка літера повинна бути замість знака питання?
(х+ 17)- 3 = 18 Г
АБВГДЕ
(8-х)+ 19 = 22 ? (Д)
5. Розшифруйте анаграми і назвіть зайве слово:
МЮЙД, ТУФ, АБОД, ТОКІЛЬ.
(Дюйм, фут, доба, лікоть. Зайве слово «доба»)
VII. Підсумок уроку.
Вчитель оцінює роботу учнів на уроці відповідно до кількості фішок, які отримав кожен учень.
VIII. Домашнє завдання.
Підготуватись до контрольної роботи. Повторити П.7-10,15-18.
№412(ст.111), 475,(ст.127), 499( ст.131)
3. Висновки.
Майбутнє будь-якої держави та людської цивілізації в цілому визначається тим, яка впроваджена в ній система освіти. Сьогодні вирішальне значення для економічного розвитку та конкурентноздатності тієї чи іншої країни, забезпечення її інтелектуальної самостійності та власного місця у сучасному, все більше взаємопов`язаному світі набувають наукові й технічні знання, високі моральні якості особистості, її інтелектуальний і творчий потенціал, винахідливість, ініціатива, почуття нового, здібність адаптуватися до умов, які швидко змінюються. Саме тому всі розвинені країни світу в останнє десятиріччя здійснюють реформування освітніх систем, основною метою якого є підвищення інтелектуального потенціалу нації, формування творчої особистості.
Боротьба за ефективність уроку є найпершим і найбільш актуальним завданням кожного вчителя. Для сучасного уроку характерними ознаками є :
- Гуманітарний потенціал і гуманізація навчання;
- Варіативність і гнучкість структури уроку;
- Спрямованість уроку на особистість учня;
- Системний підхід до архітектури уроку та процесу навчання;
- Спрямованість уроку на головне –генералізація навчання;
- Повне засвоєння матеріалу на уроці;
- Оптимізація форм роботи на уроці;
- Економія часу в шкільному навчанні.
У підготовці та проведенні уроку вчитель виконує функції сценариста, режисера, постановника та водночас є виконавцем головної ролі в написаному ним творі(Р. Сеульський).
Особливістю інтерактивного навчання є підготовка молодої людини до життя і громадянської активності в громадянському суспільстві та демократичній правовій державі на заняттях з будь – якого предмета. Це вимагає активізації навчальних можливостей учня замість переказування абстрактної, “готової” інформації, відірваної від їхнього життя і суспільного досвіду. Такі уроки дають учням основні пізнавальні та громадянські вміння, а ще навички і зразки поведінки.
Вони захоплюють учнів, пробуджують учнівський інтерес, навчають самостійного мислення та дій.
Підвищення ефективності навчального процесу, досягнення високого інтелектуального розвитку учнів, забезпечення оволодіння ними навичками саморозвитку особисто значною мірою можна домогтися, використовуючи сучасні інноваційні технології, перетворюючи традиційний урок в інтерактивний. Дотримання порядку застосування активних методик дозволяє спланувати і проводити уроки більш ефективними та цікавими для дітей.
Працюючи на уроках у парах і групах, учні усвідомлюють: людина людині – друг, а в процесі вивчення математики взаємодопомога особливо потрібна. Створення в класах “консультативних пунктів”, “пунктів швидкої допомоги”, “клубів помічників учителя” – ось дієві форми навчання і виховання дітей. Добро робити неважко, коли цього вимагає душа.
“Не будь байдужим до чужого горя “- цей лозунг постійно присутній
у класі. Від теплоти людських сердець життя здаватиметься не таким жорстоким. Дати списати домашнє завдання – це якраз бути байдужим, а допомогти зрозуміти, пояснити, надати консультацію – це зробити добру справу. Адже краса людської душі – в добрих вчинках, у допомозі людям, які потребують турботи і піклування.
“Людину роблять прекрасною працьовитість, чуйність, доброзичливість і щирість”.
- Література.
- В.Я. Романюк, Л.І.Дутко. Технології інтерактивного навчання на ураках математики. – Львів: Тріада плюс, 2004.
- О. Пометун. Інтерактивні методики та система навчання.- К.:Шкільний світ, 2007.
- Ігри дорослих. Інтерактивні методи навчання. – К.: Редакції загально педагогічних газет. 2005.
- І. Карпінська. Нестандартні уроки з математики.Тернопіль.,Підручники і посібники. 2001.
- О.І.Пометун, Л.В. Пироженко. Сучасний урок. Інтерактивні технології навчання: Наук.-метод. посібник.- К.: А.С.Л. 2004.
- Марі Бутз, Руді Фальтус, Елізабет Цохен. Робота в групах. Вибрані статті.- Львів.: Товариство Лева. 2004.
- Формирование познавательньх интересов учащихся. — М.: Педагогика, 1979. — 160с.
- Пахомова Н. Проектное обучение — что это? // Методист. -2004. -№ 1. —С. 39-46.
- Шишов С. Проектний метод: проблемы й перспективы // Учитель. - 2002. № 1. С. 39-43.
1


про публікацію авторської розробки
Додати розробку
