Інтерактивний урок на тему "Чотирикутники і мистецтво"

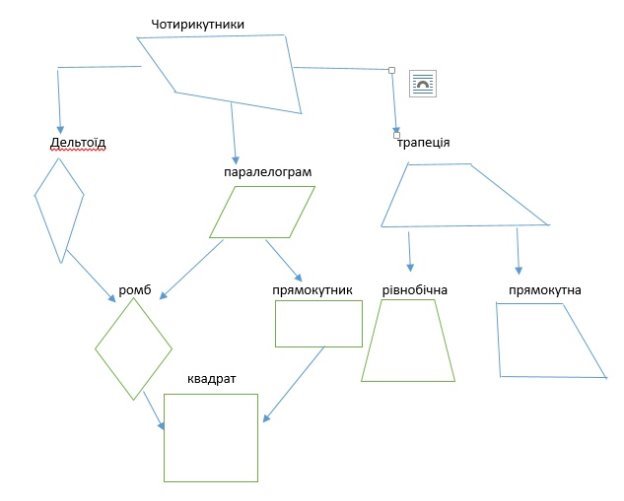
Тема: Чотирикутники

Мета:

• Узагальнити та систематизувати знання учнів про чотирикутники. Дати поняття про дельтоїд – чотирикутник, що не вивчається в школі.  Показати застосування чотирикутників у роботах художників-абстракціоністів  ХХ ст. та в архітектурі країн світу;
• Розвивати логічне мислення учнів, пам'ять, уяву, увагу, привчати до пошуку різних способів доведення;
• Виховувати творчу активність, пізнавальну самостійність та культуру математичного мовлення.

Тип уроку : узагальнення і систематизація знань, вмінь , навичок.

Обладнання: демонстраційні таблиці, презентація.

Назва уроку: «Чотирикутники і мистецтво»

«Геометрія – це прообраз краси світу»

(І. Кеплер)

Хід  уроку

    І.  Організація учнів до уроку:

1. Відгадай назву групи:

Завдання І групи : що це за чотирикутник, у якого протилежні  сторони паралельні?

Завдання ІІ групи : що це за чотирикутник, у якого лише протилежні  сторони паралельні?

Завдання ІІІ групи : що це за чотирикутник, у якого протилежні  сторони паралельні і всі кути прямі?

Завдання ІV групи : що це за чотирикутник, у якого протилежні  сторони паралельні ,а всі сторони рівні?

 Завдання V групи : що це за чотирикутник, у якого протилежні  сторони паралельні, а всі сторони рівні і всі кути прямі?

 

2. Гра «Острів правильних та неправильних відповідей»  (перевірка теоретичних знань)

Чи правильні твердження?

1.     Діагоналі ромба рівні. (ні)
2.     Якщо протилежні сторони чотирикутника рівні, то він паралелограм. (ні)
3.     У ромба протилежні кути рівні. (так)
4.     У паралелограма всі сторони рівні. (ні)
5.     Квадрат – це чотирикутник (так)

____________________________________________________________

6.     Діагоналі паралелограма рівні. (ні)
7.     У прямокутника всі кути прямі. (так)
8.     Сума протилежних кутів паралелограма 180⁰ . (ні)
9.     У ромба сума кутів, що прилягають до однієї сторони – 180⁰. (так)
10. Діагоналі ромба є бісектрисами кутів (так)

____________________________________________________________

11. Діагоналі квадрата і прямокутника рівні. (так)
12. У паралелограма діагоналі є бісектрисами його кутів. (ні)
13. У прямокутника діагоналі взаємно перпендикулярні. (ні)
14. Діагоналі ромба діляться точкою перетину навпіл (так)
15. Діагональ прямокутника ділить його на два рівнобедрені трикутники(ні)

_____________________________________________________

16. Діагоналі паралелограми точкою перетину діляться навпіл. (так)
17. Якщо діагоналі паралелограма рівні, то він прямокутник. (так)
18. Діагоналі ромба взаємно перпендикулярні. (так)
19. Середня лінія трапеції паралельна третій  основам. (так)
20. Сторони паралелограма рівні (ні)

________________________________________________________________

21. Квадрат – це ромб з прямими кутами. (так)
22.  У прямокутника всі сторони рівні (ні)
23. Діагональ прямокутника ділить його на два рівних трикутники (так)
24. Середня лінія трапеції паралельна основам і дорівнює їх півсумі. (так)
25. Якщо протилежні сторони чотирикутника належать паралельним прямим,  то він паралелограм (так)

 

 

 

3. Перевірка домашнього завдання

    Учитель. Важко уявити собі життя без чотирикутників. Розгляньте предмети побуту, окремі конструкції будівель, зайдіть до супермаркету чи в картинну галерею, - і ви побачите безліч речей у вигляді чотирикутників.

    Художники ХХ ст.. Джозеф Альберс – видатний американський мистецтвознавець-абстракціоніст, французький художник Вазарелі, голландський мистецтвознавці Тео ван Дусбург  та Модріан Піт, російський художник (дитинство та юнацькі роки якого пройшли на Україні) К.Малевич, стали початківцями створеного ними напряму в абстрактному мистецтві – супрематизму (від латинського слово supremus, що означає «найвищий»).

    Супрематизм – комбінування зафарбованих найпростіших фігур: квадрат, трикутник, прямокутник, коло.

 

Демонстрація картин

 

1. Казимир Малевич- супрематизм .Композиція в дусі супрематизму. Чорний квадрат. 1913р.)
2. Модріан Піт. - голландський художник. Його картини представляють собою поєднання прямокутників і ліній, є прикладом найбільш суворої, безкомпромісної геометричної абстракції в сучасному живописі. 
3. Тео ван Дусбург- славнозвісна «Арифметична композиція». Під час створення простої арифметичної композиції художник використав простий математичний розрахунок: сторони кожного квадрата та відстані між ними дорівнюють половині виміру попереднього квадрата.
4. Віктор Вазарелі - композиція побудована виключно на простих геометричних фігурах. Елементи картини утворюють врівноважену за кольором і формою композицію.
5. Дж. Альберс - дань поваги серії квадратів. Найбільш відомими роботами художника є серія картин, на яких зображено квадрати, написані чистими кольорами.

   ІІ. Розв’язування задач:

Учитель: З метою повторення основних властивостей та ознак чотирикутників, що вивчалися, пропоную розв’язати задачі

А) на доведення:

 

І група :Доведіть, що коли в паралелограмі всі кути рівні , то він є прямокутником.

 ІІ група : Доведіть, що коли в паралелограмі хоча б один кут прямий , то він є прямокутником.

ІІІ група : Доведіть, що коли в паралелограмі діагоналі рівні  , то він є прямокутником.

ІV група : Доведіть, що чотирикутник , у якого всі сторони рівні , є ромбом.

V група : Доведіть, що коли  діагоналі прямокутника перетинаються під прямим кутом , то він є квадратом.

 

 

Б). за малюнками:

 

1. І група. За рис.1 доведіть, що ВС=DF

 В С

 

 

 

                                                                       Е

 

 

 

 А D F

ІІ група .За  рис.2  доведіть, що АВ=СД

                     B                                      C

 

 

                                                                        

 

 

          A                                                           D

 

 

 

ІІІ група. За  рис.3                        ВЕ      СД       знайти кути трапеції 

               В  С

 75

 

 

40

А                                    Е                       Д

 

ІV група. За  рис.4  доведіть, що < АОВ=

 В                                     С

 

 

 

                                   ОО

 

 

   А                                                                          D 

  V група . За  рис. 5  знайдіть кути трапеції, якщо  що < C - <А  =

 В                                           С

 

 

 

 

 

 

 

 

 

       А                                                                    D

 

 

 

ІV. Осмислення та вивчення нових знань

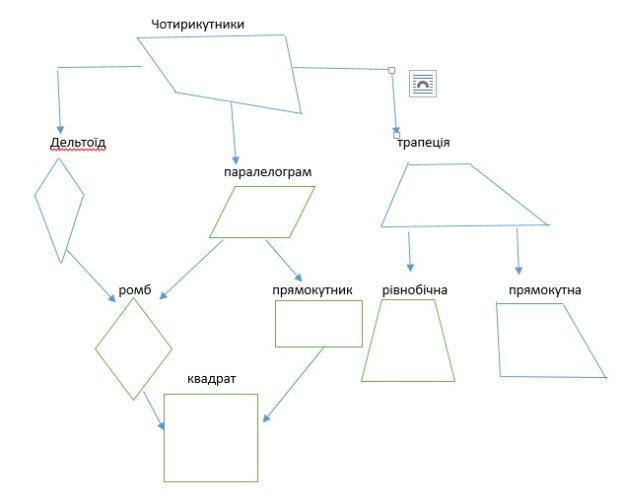
     Учитель. Додому вам було завдання дослідити ще один вид чотирикутників з попарно рівними сусідніми сторонами. Як називається такий вид чотирикутників та назвати його властивості.

    Відшукайте такі чотирикутники на малюнках:

 

 

 

 

 

 

 

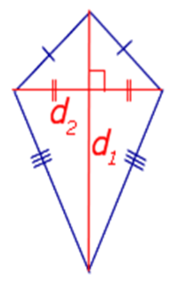
1. Означення дельтоїда

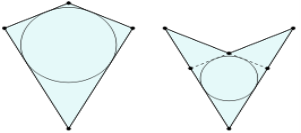
Дельтоїд - це чотирикутник, що володіє двома  парами сусідніх сторін однакової довжини.На відміну від паралелограма, рівними є не протилежні, а саме дві пари сусідніх сторін.

Опуклий та неопуклий дельтоїд

 

 

 

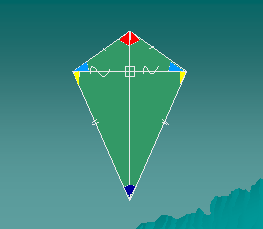
2. Властивості дельтоїда:

1. У дельтоїда внутрішні кути між сторонами нерівної довжини  рівні.
2. Діагональ дельтоїда, що з'єднує дві вершини нерівних кутів лежить на бісектрисах нерівних кутів.
3. Діагональ дельтоїда, що з'єднує дві вершини рівних кутів, являється основою двох рівнобедрених трикутників, на які вона розділяє дельтоїд.
4. Діагональ дельтоїда, що з'єднує дві вершини рівних кутів, утворює з рівними сторонами дельтоїда рівні кути.
5. Діагоналі дельтоїда перетинаються під прямим кутом і розділяють його на дві пари рівних прямокутних трикутники.

 

   

 

 

 

 

 

 

∆ δ – дельта буква грецького алфавіту. За формою цієї букви отримали назву дельтоїд, дельтовидний м’яз, дельтаплан

       Дельтаплан – літальний апарат важчий за повітря, виконаний за схемою безхвостка  зі стріловидним крилом, управління польотом якого виконується зміщенням центра маси за рахунок переміщення пілота відносно точки підвіски (балансу планера). Характерна особливість – старт з ноги і посадка на ноги.

 Дельтоїд має форму, схожу на    повітряного змія.

 

V. Закріплення набутих знань

 

Задача. Менша сторона дельтоїда АВСД – 20 см, а менша діагональ утворює з нерівними сторонами  рівні кути. Точка О – точка перетину діагоналей дельтоїда. Кут, що утворює бісектриса кута АВО з меншою стороною дельтоїда дорівнює . Знайти периметр дельтоїда АВСД.

VІ. Підсумок уроку

    Учитель. Геометрія – це не тільки школа логічного мислення, але й джерело , що сприяє розвитку асоціативного мислення. Кожен з вас намалюйте геометричну фігуру, що вам до вподоби: або квадрат, або прямокутник.

    Квадрат. Символізує такі позитивні риси характеру людини як потреба довести справу до кінця, терпіння, методичність, впорядкованість. Хто обирає квадрат, - спроможні концентруватися на головній меті.

    Прямокутник. Свідчить про перехідний стан особистості, невпевненість, непослідовність, але водночас відкритість до нових ідей, цікавість та сміливість. Вибір прямокутника, як правило, свідчить, з одного боку, про низьку самооцінку, а з іншого боку -  про довірливість.

VІІ. Домашнє завдання

      Повторити §§1-9, запитання 1-12 на стр.76, тестові завдання №3 на стр.77.